• Что такое фактурная штукатурка
• Выбираем сухие строительные смеси
• Преимущества напряженного железобетона
• Что влияет на выбор кровельного материала
• В чем преимущество пробковых полов

или, принимая во внимание (7),

(35)

Средним полным, или средним векторным, ускорением а^ называется частное , где Av-изменение скорости V за промежуток времени М, так что

с^. = д1- (36)

Полным, или векторным, ускорением а в момент t называется предел отношения (36) при 0, так что

Так как стр.-вектор, направленный внутрь кривизны кривой (фиг. 7), то и полное уско-

Фиг. 6.

Фиг. 7.

рение а всегда направлено внутрь кривизны траектории. Принимая во внимание (15), имеем также

а

(38)

или, принимая во внимание (3), имеем:

Таким образом вектор а равен сумме следующих трех компонент, направленных по осям координат:

dx .. dy .. d2z ,

*~dt* v~dt s-dTi-Модули этих векторов, равные

a, =

представляют линейные ускорения проекций точки на осях координат. При а = Const движение называется равнопеременным; при этом, если а>0, то движение называется равноускоренным, если же а <О, то движение называется равно-замедленным. При а = Const движение очевидно будет не только равнопеременным, но и прямолинейным. Далее при а = Const имеем из (34) и (7):

Jdv =Ja dt; vat + C, (39)

s = = J(af + Ci)dt lat+Ct+Cs, (40)

где Cj и Ca суть некоторые произвольные постоянные, которые м. б. определены, если величины V и S, соответствующие каким-нибудь определенным значениям t, даны. Так, если в начальный момент, т. е. при t = 0, V = Vo, S = So, то из (39) имеем Сг = Vo, а из (40) Ca = So, так что ф-лы (39) и (40) принимают следующий частный вид:

v = Vo + at, (39)

s = So + Vot1 at\ (40)

Если построить кривую, вьфажающую функциональную зависимость (34) между а и t, точно таким же способом, каким выше был построен график скорости, то мы получим график ускорения (фиг. 4). Т. к. на основании (34) и (7) между а и v существует точно такая же зависимость, как между V и S, то между графиками ускорения и скорости существует очевидно точно такая же связь, как между графиками скорости и пути. Т. о. имеем: 1) тангенс угла наклона отрезка CiPz, соединяющего две точки Ci и Са графика скорости, равняется среднему линейному ускорению за соответствующий промежуток времени; 2) тангенс угла наклона касательной, проведенной к графику скорости, равняется линейному ускорению точки в соответствующий момент; 3) площадь, ограниченная дугой Di-Da графика ускорений, ординатами, проходящими через точки t и <2, и осью t, численно равна приращению скорости за промежуток времени At от t до fa; 4) точкам пересечения графика ускорения с осью t соответствуют экстремальные точки графика скорости, а экстремальньпл точкам первой кривой соответствуют точки перегиба второй. Если в частности движение равнопеременно, то график ускорений представляет собой прямую, параллельную оси t (фиг. 8). График скорости представляет в этом случае на основании (39) наклонную прямую, отсекающую на оси v отрезок равный Vq и имеющую tg угла наклона равный

Фиг. 8.

а, а график пути на основании (40)-параболу, имеющую своей осью ось ординат и отсекающую на последней', отрезок Sq.

Пусть радиус кривизны траектории в точке А равен q (фиг. 9), а направление центра кривизны С от J. определяется ортом pi, так что

IC = QQQ. (41)

Если Tj-орт, определяющий направление касательной, проведенной к кривой в точке J. в сторону возрастания дуг, то

di - ё

(42)

где -кривизна траектории в точке А. Из (16), (42) и (7) имеем следовательно:

d d(i)Ti) dv- I di dc , di ds -df- dT -dti + * at - dt+ ds dt

dv dt

(43)

Таким образом вектор ускорения равняется сумме двух векторов

а, = .т, (44)

и

(45)

причем первый вектор имеет направление, определяемое х^, т. е, имеет направление касательной, а второй-направление ei, т. е. направление от А к центру кривизны С. Первый вектор называется поэтому танген-цдальным ускорением, а второй- нормальным ускорением. Модули этих векторов соответственно равны:

% = (44)

a. = f. (45)

а линейное ускорение

Из (43) видно, что вектор а лежит в плоскости, образованной касательной и главной нормалью, т. е. лежит в соприкасающейся плоскости. Т. к. бинормаль перпендикулярна к этой плоскости, то компонента по бинормали 5 всегда равна нулю:

6 = 0. (47)

Если точка движется прямолинейно, то е оо, и по (45) имеем = О, Так что в этом случае а = щ = ~т: и a = at = . Если к тому же точка движется еще и равномерно, то = О, т. е. = 0. Если точка движется по

окружности радиуса Б, то, так как q = R = = Const, из (44), (45) и (46) следует:

(44 ) (45 ) (46)

Ести к тому же точка движется еще и равномерно, то, так как в этом случае v = Const

и = О, из (44), (43) и (45) имеем:

4 = 0; = = Yel = R > el т. о. при равномерном круговом движении полное ускорение в любом положении точки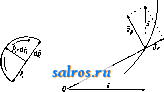

Фиг. 9.

Фиг. 10.

Фиг. И.

направлено по нормали, т. е. направление а все время проходит через центр окружности. Последнее движение представляет собой частный вид т. п. центральных движений, т. е. таких движений, при которых направление полного ускорения в любом положении точки проходит через один и тот же центр. Из формул (17), (20) и (21) имеем далее:

. dip dpi

-4-Г

dt dt

(48)

Так как 1 г^, а dpi J Pi, причем р^ и dpi вращаются от в одну и ту же сторону (фиг. 10) и так как dpi \ = dq>, то

. ni Г

dt dt 1

так что (48) принимает следующий вид: Т. о. вектор а разложен на две компоненты:

p-i-sf+Tlft. (51)

ИЗ к-рых первый, имеющий направление г^, определяет радиальное ускорение, а второй вектор, имеющий направление, перпендикулярное к первому, определяет поперечное ускорение. Так как модули этих векторов

-r-S-riSf, (50)

(51)

c,dr d4> dq> P- dtdi dt

2 dt

d<p I d2 dt2

(52)

ЧТО дает выражение a в полярных координатах г IS. (р. Секториальным ускорением II называется производная по времени от секториальной скорости v, т. ч. dv

A* = i. (53)

Принимая во внимание (30) и (5Г), имеем из (53):

1 d ldq>\ tjodr dg>,d<p\ 1 .к.. =-2 dtV Tt) = 2\df dt + d12 r = 2. (54) и так как

гйр- ка,

где к - расстояние от О до линии действия а (фиг. 11), то

/г=1а-к. (51)

Если движение центральное и если начало отсчета взять в центре движения О, то в этом случае линия действия а в любой момент должна проходить через О, и значит fc=0 и м=0, а следовательно v= Const. Таким образом при всяком центральном движении секториальная скорость постоянна, т. е., другими словами, площадь, сметаемая подвижным радиусом-вектором, пропорциональна времени. Нетрудно доказать также, что всякое центральное движение-движение плоское.

Исследовав законы движения отдельной точки, можно перейти к исследованию движения механической системы точек, т. е. такой совокупности nxj в которой движение каждой точки определенным образом зависит от двинения остальных. В частности механич. система называется системой твердой, если взаимные расстояния точек при движении системы остаются неизменными. Допустим, что система состоит из п точек. Т. к. положение каждой точки определяется 3 координатами, то положение всей системы определяется Зп координатами Xi,yi, Si,X2,yz, Zz,..., Хп,Уп, V При движении системы все эти координаты суть нек-рые ф-ии

времени i. Зависимости между точками системы обусловливаются силами взаимодействия их или связями, т. е. такими условиями движения, к-рые налагают ограничения либо только на положение точек либо также на их скорости. В первом случае связи называются геометрическими, а во втором - кинематическими. Кансдая геометрич. связь выражается ур-ием вида: /( 1, Vl, 1, Жа, t/a, 2, г„, t) = О, (55)

а кинематич. связь-ур-ием вида:

V{Xi, 2/1, Zi, х„, уп, Zn,

Допустим, что между n точками данной механической системы сувдествует к геометрических связей:

fiiXi, У1, Zi, Xft, Упу О = О

(г= 1,2,3,..., к).

Тогда из Зп координат Зп-к будут независимы, а остальные к координат определяются через них из ур-ий (57). Эти независимые координаты называются также координатами системы; число их определяет так называемую степень свободы системы <см. Координаты).

Всякое движение твердой системы точек, и в частности твердого тела, м. б. сведено к двум основным видам движения: поступательному и вращательному. Поступательным движением называется такое движение, при к-ром любая прямая, соединяющая две какие-либо точки системы, остается во время движения последней параллельной сама себе. Так, если прямая, соединяющая точки-4 и В, занимала положение J.1B1, то спустя промежуток времени она займет полояение А2В2II ABi. Так как

Дг = Дг

(58)

где

Дг = .1-а; ArsBB, Ит() = ИтрЛ,

Va = (59)

Т. о. при поступательном движении все точки системы имеют в данный момент равные скорости. Очевидно, что при поступательном движении траектории всех точек системы представляют собой конгруентные кривые. Способом, аналогичным вышеприведенному, получим, что

А = 5, (60)

т. е. что полные ускорения всех точек системы в данный момент меноду собою равны.

Вращательным двимением тела называется такое движение, при к-ром две из его точек, АиВ, остаются неподвижными. Нетрудно видеть, что в этом случае и все точки, лежащие на прямой АВ, называемой осью вращения, будут также неподвижны. При вращательном движении очевидно каждая точка, за исключением точек, лежащих на оси вращения, движется в плоскости, пер-пендику-тярной к оси вращения,по окружности, пентр к-рой находится на этой же оси.

Угол поворота Аср тела за какой-нибудь промежуток времени Д^ определяется дуговым перемещением какой-нибудь из его точек за тот же промежуток времени, вследствие чего угловая скорость со и угловое ускорение в какой-либо точки тела определяют соответственно эти же величины и для вращающегося тела. Угловая скорость м. б. вьппеуказанным способом представлена при помощи вектора О) на оси вращения тела. Пусть движущаяся точка вращающегося те.ла занимает на окружности положение А, опре-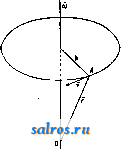

Фиг. 12.

деляемое по отношению к началу отсчета О, взятому на оси вращения, радиусом-вектором г (фиг. 12). Так как по (18) v=b со, где Ъ - радиус окружности, и так как Ъ = = г sin (со, г), то

V =0)Г sin (со, г) (61)

и следовательно

г = [(ог\. (62)

Если модули проекций вектора со на три произвольные ортогональные оси координат с началом О обозначим через р, q, г, а модули проекций г на те же оси через ж, у, z, то, пользуясь формулой проекции векторного произведения (см. Векторное исчисление), имеем:

qz-гуЛ

Vy = rx -pzy Vs=py-qx]

(63)

Это-т. н. ф-лы Эйлера. В общем случае вектор (о меняет как величину, так и направление, определяемое со, и каждому моменту времени соответствует определенная м г н о-веннаяось вращения. В частности со может менять лишь свой модуль, т. е. менять лишь свою угловую скорость, сохраняя одну и ту же ось вращения. В последнем случае вращательное движение назьшается перманентным.

Плоскопараллельным движением твердого тела называется такое его движение, когда все точки тела описывают плоские траектории, лежащие в плоскостях, параллельных некоторой неподвижной основной плоскости. В этом случае очевидно имеем: 1) все точки тела при своем двиясении остаются на неизлтенном расстоянии от основной плоскости, 2) если данное тело находится в плоскопараллельном двгокении по отношению к плоскости я, то оно находится в таком же движении и по отношению к любой другой П.ТОскости гг, парал.71ельной первой (фиг. 13). Следовательно можно основную плоскость л всегда выбрать так, чтобы она пересекала данное тело по нек-рому контуру К. Зная положение контура К на теле и в основной плоскости, можно определить и положение тела в пространстве. Т. о. исследование рассматриваемого движения тела сводится к исследованию движения контура К в плоскости.

л, т. е., что то же самое, движения подвижной плоскости р, связанной с К, в плоскости л. С другой стороны, положение плоской фигуры, ограниченной контуром К, в плоскости 71 определяется положением двух произвольных ее точек А к В или отрезком АВ, так что в свою очередь определение движения плоской фигуры К сводится к определению движения отрезка АВ в плоскости л. Отсюда нетрудно притти к следующим

Фиг. 13.

Фиг. 14.

выводам: 1) Из любого предшествующего положения плоской фигуры К, находящейся в плоскости л, можно привести ее в любое последующее положение в той м^е плоскости при помощи одного поступательного и одного вращательного движения, или наоборот. В самом деле, если первое положение фигуры определяется положением отрезка А^В^ (фиг. 14), а второе положение-тем же отрезком, но в положении А^В^, то молшо сначала переместить отрезок А^В^ параллельно самому себе до AzB[, а затем повернуть последний отрезок до положения А^В^. При первом движении отрезка плоская фигура будет перемещаться поступательно, а при втором- вращательно. Порядок этих движений очевидно м. б. изменен. 2) Из всякого положения плоской фигуры в плоскости л можно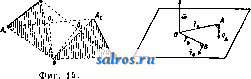

Фиг. 16.

привести ее в любое другое положение в той же плоскости при помощи одного вращения около нек-рого центра О. В самом деле, пусть имеются два положения плоской фигуры, определяемые положениями А^В^ и iLgBg отрезка АВ, так что AiBiAB (фиг. 15). Проведя прямые А-А^ и В^В^ и восставив из их середин 01 и Og перпендикуляры, получим в пересечении этих перпендикуляров точку О; AJ.iOBi= Д^аОВг, т.к. AxBi= А^В^, АгО^А^О, ВхО = В20. Т. о., вращая AAOBi около точки О, можно его привести в положение AOBz, т. е. привести А^В^ в положение-42В2. Точка О представляет собой центр вращения, соответствующий двум рассматриваемым отдельным положениям плоской фигуры. Если центр вращения соответствует двум бесконечно близким положениям плоской фигуры, то он назьшается мгновенным. Мгновенный центр вращения занимает определенное положение как в плоскости я, так и в плоскости р, переме-

щающейся вместе с фигурой. Т. к. движение плоской фигуры состоит в непрерывном переходе от одного положения к бесконечно близкому к нему другому полол^ению, то этому движению соответствует бесконечно большое число мгновенных центров вращения, непрерывно следующих друг за другом. Геометрич. место мгновенных центров вращения в плоскости л называется неподвижной полодией, или центроидой, а в п.чо-скости р-и сдвижной полодией. Эти кривые соприкасаются всегда в точке, представляющей мгновенный центр вращения в данный момент. Если же бесконечно малое вращение происходит около мгновенного центра вращения О2, то принадлежащие плоскостям лир две точки 0[ и О , совпадавшие в предшествующем центре вращения Oi, разойдутся; при этом 00 = OOz; это указывает на то, что нри движении плоской фигуры подвижная полодия перемещается, и притом без скольжения, по неподвижной полодии. Каждому определенному движению фигуры соответствует определенная пара полодий. Если подвиж;ную полодию сделать неподвижной, а неподвижную-подвижной, то движение плоскости л по отношению к р называется движением обращенным по сравнению с первым. В общем обращенное движение совершенно отлично от данного. Так, если прямая перемещается в плоскости, касаясь данной окружности, то каждая точка подвижной плоскости описывает эвольвенту круга, а если, наоборот, окружность катится но ирямоа, то каждая точка плоскости описывает циклоиду. Траектория какой-либо точки подвилсной плоскости р по отношению к неподвижной л называется рулеттой.

Угловая скорость вращения плоскости р около мгновенного центра вращения называется мгновенной угловой скоростью. Очевидно все точки плоскости обладают в данный момент одной и той же мгновенной угловой скоростью. Пусть имеем в плоскости р две точки А и В, положение к-рых относительно системы отсчета с началом в мгновенном центре вращения О определяется и , Из ур-ия (62) имеем:

= а! ,Vb = [со Гд] , (64)

где Va и Vs-скорости точек А и В в данный момент (фиг. 16). Т. к. co L и ш J. г^, то из уравнения (64) имеем также: Va = (ог, Vbojts и

.- = Г- (65)

в

Т. о. из ур-ий (64) и (65) имеем: 1) скорости всех точек плоскости р перпендикулярны к прямым, соединяющим их с мгновенным центром вращения; 2) величины скоростей пропорциональны расстояниям от соответствующих точек до мгновенного центра вращения. Отсюда следует далее, что концы векторов скоростей для точек прямой, проходящей через мгновенный центр вращения О (фиг. 17), лежат на прямой, также проходящей через О, т. к. лишь в этом случае величины векторов скоростей Vi, Va, ... пропорциональны расстояниям А-О, А2О, ... Если повернуть векторы скорости Va и Vq (фиг. 18) в одну и

ту же сторону на 90°, то получаются т. н. ортогональные скорости vJHV. Т. к. на основании ур-ия (65)

-Л^ то -4 = .

л

Отсюда следует, что, соединив концы А'я В' ортогональных скоростей, получаем прямую А'В', параллельную АВ. Это соображение дает легкий способ построения скорости и любой другой точки С. Для этого достаточно соединить С с А я В я яз точек А' я В'

провести прямые А'С II АС и А'В' II АВ; ->

СС = -уедает ортогональную скорость точки С, так что, повернув vcна 90° в сторону, противоположную прежней, получим i;;. Очевидно, если С лежит на J.B, то С' лежит kslAB. Т. о., если прямая д (фиг. 19) не проходит через мгновенный центр вращения, то концы векторов ортогональных скоростей точек прямой д лежат на одной прямой, параллельной д, причем все ортогональные скорости пересекаются в точке О. Проектируя ортогональные скорости vj, Vg, Vo, ... на перпендикулярное к д направление д^, получим одинаковые проекции, и т. к. эти скорости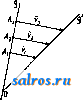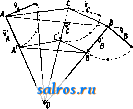

Фиг. 17.

Фиг. 18.

суть повернутые на 90° истинные скорости va, Vb, Vc и т. д., то проекции последних по направлению д также равны между собой.

Что касается ускорения точек плоскости р, то, так как по ур-ию (46) ускорение каждой точки зависит от радиуса кривизны q ее траектории, необходимо предварительно рассмотреть зависимость между q и другими элементами движения. Возьмем какую-нибудь точку плоскости, перед1ещающуюся по траектории Т (фиг. 20), и рассмотрим два бесконечно близких положения ее при увеличении времени на величину dt. Нормали АК я А'К, восставленные к Т в точках А и А', пересекаются в центре кривизны К и пересекают неподвижную полодию *S в точках Р и Р'. Пусть АР=1;РКс; PP=do; АА = ds; далее АКА' = dr; АРА' = dgi; 4-NPA = а, где NP нормаль к S в точке Р. Проведя радиусом КР дугу РВ, имеем:

у- РВ da COS g ЁР с \7~АА~ ds ~Ш Т±

причем знак минус следует взять, если К лежит между Р и -4; так как ds = 1 dq>, то

der cos а с /1 1\ dv 1 ,пгч\

d--r-Tc (с ± l) а = g = ,. (67)

Величины в левой части ур-ия (67) зависят от выбранной на плоскости р точки, в то время как 0 имеет в данный момент одно и то

нее значение для всех точек вращающихся около мгновенного центра Р. В следующий

момент изменит в общем свое значение, но новое значение опять будет одним и тем

d<P

же для всех точек р, так что ~ есть нек-рая

ф-ия от Т. к. г и а суть полярные координаты точки А, то геометрич. место точек, для

к-рых Const, есть проходящая через

точку Р окружность с центром на нормали N,

к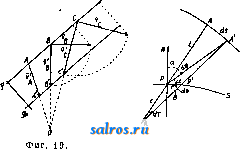

Фиг. 20.

Из ур-ия (67) видно, что и

COS в

в данный

момент также постоянно для всех точек, для которых и Const, т. е. представляет

также окружность. Обе эти окружности соприкасаются в той же точке Р, что и полодии. Т, о. центры кривизны траекторий всех точек, лежащих на окружности, проходящей через Р, также ленсат на окружности, проходящей через Р. В частности, если РК= = с=сэо, то из ур-ия (67) имеем:

COSa

(68)

что представляет собой геометрич. место точек, траектории которых имеют в данный момент q=oo, Т. е. точек, проходящих в данный момент через точки поворота. Геометрич. место точек, представляемое ур-ием (68), есть окружность диаметра d, проходящая через Р и называющаяся поворотным кругом. Соответствующая поворотному кругу окружность = Const пре-

COS (X

вратилась в бесконечно удаленную прямую. Если на поворотном круге взять какую-ни-/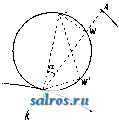

Фиг. 21.

Фиг. 22.

будь точку W (фят. 21), то т. к. мгновенное вращение точки W происходит около Р, т. е. в направлении, перпендикулярном к WP, отрезок TToW, дающий направление поворотной касательной, проходит через TFq-крайнюю точку диаметра d поворотного круга, называемую полюсом поворота. Т. о. все поворотные касательные проходят через точку Wq. Проведя из точки А

плоскости р прямую АР, на которой лежит и центр кривизны К траектории Т, и обозначив PW = u, имеем u=d cos а, а из уравнения (67) получаем:

или

1±JC

с

(69)

что дает возможность найти q и К для точки А, если W ж Р известны; для этого следует соединить какую-нибудь точку Q с точками А, W и Р (фиг. 22) и провести из Р прямую PRWWQ до ее пересечения с в точке R, затем из R следует провести RWKPQ до ее пересечения с АР в точке К, к-рая и представляет собой центр кривизны. В самом деле,

AR QR

АР WP

Скорость W, с какою мгновенный центр вращения перемещается по S, равняется

da dt

так что

-dt-

(70)

dg>

dt

Эту скорость не следует смешивать со скоростью точки Р, принадлежащей плоскости р и имеющей скорость равную 0. С другой стороны, имеем:

(71)

так что, деля (70) на (71), имеем на основании ур-ия (67):

d=. (72)

т. о. скорость перемещения мгновенного центра вращения равняется произведению

Фиг. 23.

Фиг. 24.

из диаметра поворотного круга на мгновенную угловую скорость.

Пусть скорость точки А равняется v, так что г> ±АР, а ускорение равно а. Разлагая а на две компоненты: -по направлению АР, а щ - по направлению перпендикулярному, имеем наоснованииур-ия(45):

(73)

2 ЛР2 -0)2

!2a)2

или, т. к. на основании ур-ия (69)

AWl~u =

то = AW-о); с другой стороны, AW = = АР - WP = l - d cos а, так что на основа-кии ур-ия (72)

= (I - d cos а) со = 1о)- WCO cos а. (74)

Из ур-ий (44) и (18) имеем также:

dv d(a)0 dl , doi

(77)

dt dt

При перемещении точки из в Л' прямая А'К пересекает S уже в новой точке Р', так что \иРР' = da, а отрезок I = АР уменьшается на величину Р'Е = dl (фиг. 23); следовательно

dt d<T . . , .

J = - sm а = - w sin а = - со d sin а.

Таким образом

at=-l -d -(о^ sin а =-ie-woi sin а, (75)

где В-мгновенное угловое ускорение плоскости р, или, пользуясь (44) и (45), имеем из (74) и (75):

а = (Zco2 - WW cos а) 4- (}д - wco sin a) = = Zcopi-Ь Z0Ti -wcocos a-pi -wcosin a-Tj. (76) T. 0. a состоит из трех компонент (фиг. 24): ai = ?coei I

3 = - woi cos a Pi - wco sin a j причем первый вектор направлен по нормали в сторону , второй-по касательной в сторону Ti, а третий, в свою очередь, имеет одну компоненту в сторону, противоположную ei, a другую-в сторону, противоположную Ti. Нетрудно видеть, что щ параллелен диаметру PW поворотного круга, направлен от Р к Wq и имеет модуль аз = wco = d 0)2. (77)

Так как = , то, взяв результирующую

w = i + 3 получим вектор, направленный от А к W(f, причем

а^ = 2Жо-со-. (78)

Т. о. полное ускорение м. б. представлено еще и как сумма двух векторов а^, и щ:

а^а^ + щ. (79)

Ускорение назьшается полюсным ускорением. Модуль 3, как видно из (77), один и тот же для всех точек. Это есть в то же время ускорение той точки плоскости р, к-рая совпадает с Р и к-рая имеет следовательно скорость=0. Ускорение называется поворотным ускорением. Т.к.всем точкам поворотного круга соответствуют радиусы кривизны их траекторий равные оо, то поворотный круг есть в то же время геометрич. место всех точек, нормальные ускорения к-рых а„ = = 0. Для того чтобы найти

геометрич. место точек, для к-рьгх тангенциальные ускорения равны О, т. е. для к-рых а< = 0, имеем из (75):

Z0-d-c 2sina=O; h. (75)

Так как в правой части (75) имеется выраяге-ние, постоянное для всех точек р, то (75) представляет собой окружность, диаметр которой h = перпендикулярен к нормали N

и проходит через Р. Из сравнения (75) и (68) видно, что найденная окружность, называющаяся кругом перемен, пересекает

поворотный круг в нек-рой точке В, не имеющей ни тангенциального ни нормального ускорения, т. е. в точке, полное ускорение к-рой равняется нулю. Точка В называется поэтому центром ускорений. Определение центра ускорений В имеет большое значение при определении ускорений точек плоскости р. Так как 4- WPB = 4- WHP = j8 (фиг 25), то из (75) имеем:

Ускорение а точки А можно разложить на две компоненты а' и а по направлению АВ и по перпендикулярному к АВ направлению, для чего, разложив и щ по этим двум направлениям, сложим соответствующие компоненты. Обозначая

4WoPA = a\ 4-WoPB4.WJIP==fi; 4ВАР = у\ 4LBP = 6, имеем, принимая во внимание (74), (75) и (72):

а' = ttn cos у - ttf sin у = (lo) - wco cos a) cos у - - (IQ - wco sin a) sin у = l(co cos у - в sin y) - - da)2 cos (a-j-y), (79)

a = a sin у -{-щ cosy = Цсо^ sin у + в cos у) - ~d-co sin (aу). (80)

Опуская из P перпендикуляр на AL, имеем: PL = г sin у = BP sin (5 = d cos sin (5. (81)

Принимая BO внимание (81) и (75 ), имеем из (79) и (80) после соответствующего преобразования:

а'= (? COS у-d cos Д cos (5), (82) а = в (I cosy-d cosрcos S). (83) Ho выран^ения, стоящие в скобках правых частей последних равенств, равняются

А В = е, так что окончательно имеем:

а' = еа>2, (84)

а = е9, (85)

a=eVoJ+вK (86)

Кроме того

tg/?.

Из (86) видно, что величина ускорения любой точки плоскости р пропорциональна расстоянию е точки до центра ускорения, а направление полного ускорения образует один и тот же угол /9 с прямой, соединяющей точку с центром ускорения.

Возвращаясь к плоскопараллельному движению тела, нетрудно притти к заключению, что мгновенному вращению плоской фигуры около мгновенного центра Р соответствует мгновенное вращение тела около оси, перпен-дику.пярной к ?г и проходящей через точку Р. Т. о. подвижной и неподвияшой полодиям соответствуют две цилиндр, поверхности, пе-ресехсаемые плоскостью л ортогонально, так что в сечении получаются данные полодии. Ци.тиндрич. поверхность, проходящая через подвижную полодию, называется подвижной аксоидой, другая же поверхность называется неподвижной аксоидой. Плоскопараллельное двияение тела происходит следовательно так, как будто подвижная аксойда, неподвижно скрепленная с телом, катится без скольжения по непод-

вижной в пространстве аксоиде, причем общая образующая представляет в данный момент мгновенную ось вращения. Если данное тело движется так, что одна точка О остается неподвижной, то, описав в теле около этой точки О шаровидную поверхность S,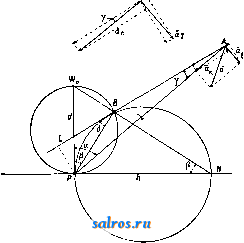

Фиг. 25.

можно определить положение тела в пространстве, зная положение S, так что изучение движения тела сводится к изучению движения поверхности S. Пололсение же последней определяется положением дуги большого круга, проведенной по шаровой поверхности между двумя какими-либо точками последней. Пусть эта дуга перешла за какой-нибудь промежуток времени каким-нибудь образом из положения А^В^ в положение А^В^ (фиг. 26). Соединив точки А^, А2 и В^, В2 дугами большого круга и восставив к серединам Ci, Са последних перпендику-.яярные дуги большого круга, найдем не к-рую точку О' пересечения пос-.ледних, находящуюся также на поверхности S. Соединив О' с Ai,Bi и с А 2, В2 дугами большого круга, получим два, равных сферических тр-ка А^О'Вг и А,Р'В2. Закреп-тяя точку О' на поверхности iS , можно, вращая тр-к A-Jj В^, привести его в положение A20B2 что очевидно равносильно вращению всей шаровой поверхости S около оси О'О. Т. о. из всякого любого предшествующего полон^ения в любое последующее можно рассматриваемое тело прхгеести при помощи одного вращения около нек-рой оси, соответствующей этим двум положениям. Если тело переходит из одного полоноения в бесконечно близкое к нему другое положение, то соответствующая ось вращения назьшается мгновенной. При движении тела мгновенные оси вращения, проходя через точку О и следуя непрерьшно друг за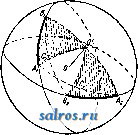

Фиг. 26.

(86)

другом, образуют в пространстве нек-рую конич. поверхность с вершиною в О, нред-ставляюшую неподвижную аксоиду. Геометрич. место мгновенных осей вращения в самом теле, т. е. подвижная аксоида, представляет очевидно также конич. поверхность с вершиной в О (фиг. 27). Т.о. движение тела, имеющего неподвижную точку О, м. б. осуществлено качением без скольжения двух конич. поверхностей, имеющих свои вершины в О и касающихся по прямой, представляющей мгновенную ось вращения (см. Волчок). Т. к. все точки мгновенной оси имеют скорость равную О, то для них имеют место согласно (62) и (63) соотношения:

[cor] = О qz - ту = 0 гх - pz = О ру - qx = 0

где x,y,z-координаты произвольной точки мгновенной оси относительно неподвижных в пространстве осей. Из (86) имеем ур-ия мгновенной оси вращения:

= = . (87)

р q г

Рассмотрим свободное твердое тело, перемещающееся в пространстве. Положение тела определяется положением трех его точек, не лежащих на одной прямой, т. е. положением нек-рого тр-ка А^В^Сх. Пусть тело пришло из положения, определяемого тр-ком А^В^Сх, в положение,определяемое треугольником ABCz (фиг. 28). Из первого положения во второе можно было бы привести тело след. обр.: переместив тело поступательно по направлению А-А до совпадения точек А^к Az так, чтобы тр-к А^В^С^ занял положение AzB[C[, повернуть затем тело около нек-рой оси, проходящей через А^ так, чтобы тр-к AzBiC[ совпал с тр-ком ABCz, что на основании изложенного всегда представляется возможным. Т. о. свободное тело можно всегда привести из одного положения в другое при помощи одного поступательного и одного вращательного движения, причем порядок следования движений роли

Фиг. 27.

Фиг. 28.

не играет. Отсюда следует, что и бесконечно малое перемещение тела м. б. представлено бесконечно малым вращением и бесконечно мальпл поступательным движением, которые могут происходить одновременно. Совокупность поступательного и вращательного движений назьшается винтовым движением. Ось вращения называется осью винтового движения. Если эти движения бесконечно малы, то винтовое движение называется мгновенным. Т.о. при своем движении свободное тело в каждый момент совершает нек-рое мгновенное винтовое движение, причем в общем винтовые оси меня-

ют свои полонсения как в самом теле, так и в пространстве. Геометрич. место винтовых осей, т. е. подвижная аксоида, представляет собой нек-рую линейчатую поверхность, соприкасающуюся по прямой с другой линейчатой поверхностью - неподвижной ак-соидой. Общая образующая представляет собою мгновенную винтовую ось. Примером таких линейчатых поверхностей могут служить два однополостных гиперболоида, соприкасающихся по одной прямой (фиг. 29), причем если один из них неподвижен, то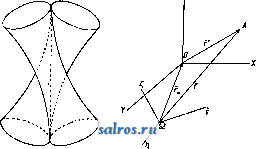

Фиг. 29.

Фиг. 30.

другой может перемещаться по поверхности первого, совершая около общей образующей бесконечно малое вращение и скользя в то же самое время вдоль нее, вследствие чего мгновенная винтовая ось назьшается также мгновенной осью скольжения-вращения (см. Винт в теоретич§ской механике и Мбторное исчисление).

Пусть некоторое тело перемещается по отношению к некоторой системе отсчета Oxyz, которая вместе с телом перемещается по отношению к системе отсчета С, так что каждая точка тела принимает участие в двух движениях: по отношению к Oxyz и вместе с последней системой по отношению к . Движение тела по отношению к первой системе называется относительным, движение Oxyz по отношению к -и е-реносным, а двилгение тела по отношению к -движением сложным. Два первых движения называются составляющими движениями. Число составляющих движений м. б. и больше двух. Скорости в этих двргжениях носят соответствующие этим движениям названия: относительной, переносной и сложной скоростей. Пусть радиусы-векторы, определяющие полол^ение А по отношению к Oxyz и Qrj будут г' и г, а радиус-вектор, определяющий положение О по отношению к будетГд (фиг. 30), т. ч. г = г' Го,

откуда имеем:

dr dr

di~dt dt

Обозначая относительную, переносную и сложную скорости точки А тела соответственно через Vy, Vg и v, имеем:

dr dro. dr

(88) (89)

dt dt

так что из (89) имеем:

(90)

(91)

т. е. вектор скорости в сложном движении равняется сумме векторов скоростей состав-

ляющих двинений. Составляюпщми движениями м. б, движения поступательные, вращательные, винтовые и т. п. При различных видах составляющих движений получаются различные виды сложных двилгений. Пусть тело в своем относительном движении перемещается поступательно со скоростью v, а система Oxtfz вместе с телом движется также поступательно, но со скоростью v. Т. к. и v-i в данный момент постоянны для всех точек тела, то каждая из них такясе имеет одну и ту же сложную скорость v, т. е. сложное движение также поступательно. Если составляющие движения представляют собой мгновенные вращения, векторы мгновенных угловых скоростей к-рых суть со к ш^, то могут представиться такого рода случаи: 1) оси вращения пересекаются, 2) оси вращения параллельны и 3) оси вращения перекрещиваются. Если оси вращения пересекаются, то, рассматривая скорость вершины А (фиг. 31) параллелограма, построенного на и cog, смещенных в О, имеем из (62):

(Vi)=[wirJ и (2)л = [ 3 так что

где

Га = OA,

но так как

[согГА] = - К aI, то Va = О, так что А в данный момент находится в покое,-другими словами, вся прямая OA также находится в покое, и следовательно слолсное двюкение представляет собою мгновенное вращение, происходящее около диагонали OA. Пусть мгновенная угловая скорость сложного движения равна £i. тогда скорость сложного движения какой-либо точки М будет

ж= >L (91)

с другой стороны, по (91) имеем:

Vjf = [MiVjI + [ft)2 Гм1 = [(Wi + СО2) rjf]; (92)

сравнивая (9Г) и (92) получаем:

i2 = Q)i-fa)2. (93)

Обобщая этот результат для случая п составляющих мгновенных вращательных двилсений, можно написать:

= (г =1,2,3, ...,п).

(94)

Пусть далее cow щ и направлены в одну и ту же сторону. Проведем плоскость, перпендикулярную к 1, пересекающую coi в точке А^, а cog-в точке А2 (фиг. 32). На прямой A-iAz можно найти такую точку А, к-рая имела бы в данный момент сложную скорость, равную нулю. В самом деле, пусть С-некоторая точка на А^А^; тогда скорость относительного движения С будет (Vi)cr =

= lcoiAiC], а переносная скорость (v2)c =

= [(02 -гС], причем направления этих векторов противоположны, т. о. для нахождения А имеем:

(Ог-А,А = 0)2-А2А, или. = 1=. (95)

так что А делит AAz внутренним образом на части, обратно пропорциональные o>i и Og. Очевидно все точки, лежащие на прямой AD\[(Oi, имеют также v = О, так что AD есть мгновенная ось вращения сложного движения. Пусть мгновенная угловая скорость сложного вращения равняется £i. Рассматривая точку -4-2, имеем для нее:

{v)a = АА2, (Vi)a, = Oil A2l ( 2)4, = 0.

Таким образом £i АА2 = o>i А1А2, или на основании (95):

AiA + AzA]

А.А

AAi AAJ

ft)i -{- 2 ; i2 = CUi -f (Wj .

Если Oil и 2 антипараллельны, то точно таким же образом получаем, что точка А де-

Фиг. 31.

Фиг. 32.

лит отрезок .4i 2 внешним образом на части, обратно пропорциональные со и cog, и что £i = oi2 - со1(если ai2 > (Oi). В последнем случае, если со2= - coi (пара вращений), то мгновенная ось вращения удаляется в бесконечность, и тело в своем сложном движении перемещается поступательно со скоростью, перпендикулярной к плоскости, образованной и соа-В самом деле, для какой-либо точки М тела имеем (фиг. 33):

V = [Oil PiM] -f к РаМ] = [oiiiPiM -РаМ)]

= К Р1Р2] п voiiР1Р2. (96) Точно такую же скорость v будет иметь и любая другая точка тела. Отсюда следует,

Фиг. 33.

Фиг. 34.

ЧТО всякое поступательное движение тела м. б. рассматриваемо как составное движение пары вращений.

Пусть далее одно из составляюпшх движений будет мгновенное вращение, а другое движение-поступательное, перпендикулярное к мгновенной оси вращения. Заменим скорость V поступательного движения парою

вращений oi и соа так, чтобы Oi = < = -eoj (фиг. 34), причем на основании (95) имеем:

т. к. (02 = -со, то эти два вращения взаимно уничтожаются, и остается одно вращение

Т. о. сложное движение в данном случае есть мгновенное вращение, происходящее с мгновенной угловой скоростью, равной данной, но около оси, параллельной первой

и отстоящей от нее на расстоянии . Если

мгновенная ось вращения не перпендикулярна к скорости V поступательного движения, образуя с последней угол а, то раз-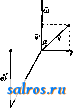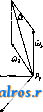

Фиг. 35.

Фиг. 36.

ложив V на два составляющих поступательных движения со скоростями v и v -первое по направлению (И, а второе по перпендикулярному направлению-имеем v = v cos а; и = г; sin а (фиг. 35), В свою очередь движения V и со м. б. заменены одним мгновенным вращением со II со и отстоящим от со

, V и-sin а

на расстоянии d = - = ---; в окончательном итоге имеем сложное движение, состоящее из поступательного движения со скоростью V и^гновенного вращения с угловой скоростью со, причем соII v, т. е. получаем мгновенное винтовое движение.

Пусть наконец имеются два мгновенных вращения с угловыми скоростями со и cog, на-

Фиг. 37.

Фиг. 38.

правления которых перекрещиваются. Перенося соа параллельно самому себе в точку приложения Pi вектора coj, прибавим в то же время поступательную скорость vcog (фиг. 36). Мгновенные вращения coj и cog заменим одним вращениемiScoi+cog. Т. о. имеется вращение Q и поступательное движение V, к-рые м. б. заменены, как выше было доказано, одним винтовым движением. Обобщая вышеприведенные результаты, можно сказать, что если имеются п мгновенных составных вращения coi, cog, ..., co,j и m составных поступательного движения ii, г>2, ..., г', , то, заменив все составляющие вращения одним результирующим вращением й (фиг. 37), а все поступательные движения одним результирующим поступательным движ;ением со скоростью V, заменим затем й и v одним результирующим винтовым движением.

Определение полного ускорения точек тела при сложном движении последнего м. б.

произведено след. обр. Пусть обе системы отсчета О и i2 имеют одно общее начало и пусть мгновенная угловая скорость вращения системы О будет со; скорость какой-либо точки А, определяемой радиусом-вектором складывается из переносной скорости [cor] и относительной скорости v, равной ~, где знак () указывает на то, что изменение рассматривается по отношению к системе О (т. п. локальная производная). Т. о.

Так как всякий другой вектор b = b(t) м. б. рассматриваем как радиус-вектор конечной точки его, то и по отношению к 6 м. б. применено соотношение (97), т. е.

=[-6]+- (97)

Если же начало О не совпадает с началом

-> -> то, обозначив О Л = г, f20 = Ро и £iA = Q (фиг. 38), имеем:

е = 9о + г. (98)

Отсюда на основании (97) имеем:

= i = # +1 З + = г^о + [ + , (99)

где Vq - скорость точки О. Беря производную по t от (99) и применяя к v,. и * ф-лу (97), имеем:

d ( 1 г п I , dv~ dvo , Гй(а 1 , dr

или же, так как = ir имеем после приведения:

df +

Ldf }

-Ь [со [cor]] -Ь

+ 2[cov,]

(100)

Если бы не было относительного движения, то, так как v,. = О, ускорение а равнялось бы ускорению переносного движения , и следовательно

d o .

представляет тельное ускорение

d df

очевидно

(101) относи-

(102) (103)

Таким образом

о. = 4- -f 2 [со V,.];

последний член правой части (103) представляет т. н. добавочное или поворотное (кориолисово) ускорение , так что

a, = 2[cov] (104)

и

с = 2со V,. sin (со, Vr). (105)

Динамика точки. До сих пор явления движения рассматривались нами вне зависимости от причин , вызывающих их, т. е. вне зависимости от тех факторов, без наличия которых данное движение не могло бы