• Что такое фактурная штукатурка
• Выбираем сухие строительные смеси
• Преимущества напряженного железобетона
• Что влияет на выбор кровельного материала
• В чем преимущество пробковых полов

нацией и напряжением существует линейная зависимость, к-рая остается постоянной при любом знаке и любой величине напряжения (закон Гука). Это условное предположение в определенных пределах достаточно близко соответствует действительным явлениям в таком материале, как сталь, и значительно менее близко к действительности в отношении таких материалов, как чугун, камень, дерево и др. Все перечисленные выше гипотезы являются основными и для теории упругости. Специальной гипотезой М. с. является предположение, что плоские сечения, нормальные к осп бруса, остаются плоскими и после деформации в том случае, когда действие внеиших сил вызывает в .тих сечениях только нормальные напряжения (гипотеза Бернулли). Это предположение в отногиении брусьев прямых или малой кривизЕхы приводит к другому положению, именно-к гипотезе изменения нормальных напряжений по закону плоскости (гипотеза Навье).

Очевидно, что выводы М. с, основанные на перечисленных рабочих гипотезах, применимы только с определенными ограничениями именно лпп1Ь к тем случаям, в отношении к-рых сделанные в этих гипотезах предположения оправдываются с достаточной степенью точности. Пре^кде всего поэтому выводы М. с. лтогут применяться к явлениям лишь в пределах упругости, т. е. только прп таких напряж:ениях, при которых остающиеся деформации практически равны нулю. Затем М. с. ограничивает свою задачу только такими явлениями, которые сопровождаются малыми деформациями и малыми по сравпегшю с общими размерами тела относительными перемещениями. Это ограничение позволяет считать, что деформации, вызываемые одной системой сил, не вызывают изменений в действии другой системы сил, приложенной к тому же соорунсению. Отсюда в свою очередь вытекает возмояс-ность определять совокупное воздействие нескольких систем сил на тело как сумму воздействий каяадой системы в отдельности. Это свойство аддитивности воздействий обычно носит название принципа слг)жения действия сил или независимости действия сил и является одним из важнейших принципов дисциплины. Следует однако отметить, что в число случаев, рассматртгваемых М. с, входят также и такие, где принцип этот нарушается. К таким особьш случаям относится напр. продольный изгиб, совместное действие изгиба и сжатия и др. Указанные выше ограничения принимаются также и теорией упругости. Соответственно же указанной выше специальной гипотезе М. с, именно гипотезе Бернулли, эгой дисциплиной вводится и дополнительное ограничение своих задач, именно рассмотрению подвергаются лишь такие тела, поперечные размеры к-рых малы по сравнению с д.липою тела. Только в отношении таких тел, называемых брусьями или стержнями, гипотеза п.лоских сечений оправ,и>шается с достаточной для практики степенью точности. К сожалению, выводами М. с. нередко пользуются и вне рамок ее действительной применимости. К подобной экстраполяции mojkho прибегать только в качестве первого приближения и

всегда счедует учтггьтать при этом возможность к[)упных ошибок и погрешностей.

Общая схема пост])оенич М. с. может быть представлена в следуюш;ем виде* I. Теория внеиших сил. Плоские и пространственные системы сил. Неподвижная и подвижная нагрузка. П. Теория отдельного статически оп1эеделимого бруса (сопротивление мате-риатов): а) теория сечения; б) основные явления в брусе в их чистом виде; чистые растяжения, катие, сдвиг, изгиб, кручеггие и местное действие сил; в) комбинированные явления; косой изгиб, совместное растяясе-ние и изгиб и т. д.; г) построение изгибов, основанное на свойствах диференциального уравнения упругой лпнии. III. Теория статически определимого шарнирио-стержнево-го сочетания брусьев (статика соору^кений):

а) аналитич. определение усилий в фермах;

б) гра4>ич. определение усилий; в) в.шяние подвижной нагрузки; г) прострапственпь^е шарнирно-стерлсневые системы. IV. Ocnttn-ные теоремы о переменщниях в упругих системах. V. Расчет статически неопределимых систем. VI. Вводные главы М. с: а) динамическое действие сил; б) продольные изгибы;

в) статика сыпучих тел.

В первом разделе этой схемы изучаются нагрузки, действующие на тела, даются способы нахождения реактивных сил и исследуется характер воздействия совокупности активных и реактивных сил на сооружение. Рассматриваемые в М. с.действующие на сооружение нагрузки м. б. подразделены на нагрузки объемнЕяе, т. е. распределегшые по объему тела; поверхностные, т. е. действующие на определенную поверхность; линейные, т. е. распределенные по длине оси бруса, и сосредоточенные. Так как пртрода всякой нагрузки всегда материальна, т. е. связана с объемом, то в строгом смысле слова все нагрузки принад л ежат к числу объемных. Все же остальные из перечисленных категорий нагрузок являются по существу услов-ны.м схематич. изображением действия сил на тело. В виду малых поперечнььх размеров бруса обычно пренебрегают тем обстоятельством, что фактически наг[)узка бывает приложенной по поверхности бруса, и относят ее непосредственно к оси бруса, т. е. к линии, соединяющей ц. т. поперечных сечений тела. Только в отдельных монографиях (Бел-зецкий, Руднев и нек-рыэ др.) учитьлвается влияние переноса нагрузки с поверхности на ось. Ось бруса и является тем ус.тов1п>гм расчетным сооружением, к которому относят действие внешних сил. В виду того что М. с. ограничивается только рассмотрением случаев с малыми перемещениями, представляется возмоясным считать внепшие силы приложенными к оси бруса в ее недеформиро-ванном состоянии. Это обстоятельство позволяет к условиям равновесия упругих тел применять все те правила и положения, K-pi>ie даются в теоретич. механике для абсолютно твердых неизменяемых тел. Поэтому для слолсения, разложения и переноса сил, приложенных к сооружению, М. с. пользуется всеми графич. и аналитич. приемами, известными в механике теоретической (см.). К специальным практическим приемам М. с. для сложения сил, лежащих в одной пло-

скости, нужно отнести метод т. и. веревочного многоугольника (см.), хотя это построение иногда изучается и в курсах теоретической л1еханики. Для плоской (лютемы сил теоретич. механика дает, как известно, тррг ур-ия равновесия, иначе говоря, три условия д.тя нахождения реактивных сил. Т. о. сооружение, представляющее собой один лсесткин диск, является статически определимым относительно реакции опор в том случае, ес-.ти реакции опор содержат три и не более трех непзвестиых. Наиболее частой комбинацией опор для плоского статически определимого сооружения являются две опоры, именно шарнирно-пеподвигкная опора и шар-иирно-подвнжпая опора. В последнее время все больше входит в употребление условное изображение реактивных устройств при по-.ющи опорных стерженьков. Определехше реакций сводится к разлолсению равнодействующей внешних сил на три непересекающиеся в одной точке составляющие по направлениям трех опорных стерлченьков. Для статически определимой относительно реакций опор л^есткой пространственной системы для закрепления к опорам необходимы 6 опорных стержней, не пересекающихся по одной прямой, соответственно 6 условиям равновесия пространственной системы сил. После того как будут опреде-.гены реакции опор, представляется возмолх-ным перейти к исследованию действия совокупности внешних сил на брус. В этом исследовании элемент ds бруса в любом мысленно проведенном сечении рассматривается как звено, соединяющее две группы активных и реактивных сил, именно группу сил, находящихся левее сечения, и группу сил, находящихся правее сечения. Действие этих двух групп сил на элемент ds сводится в общем случае к нормальной силе Ng, вызывающей растяжение или слгатие, моментам Мд. и My, вызывающим изгиб элемента вокруг осей X и Y, лежащих в плоскостях сечения и являющихся главнылп! осями инерции сечения, поперечньш силам Qrn Qy, вызывающим сдвиги, параллельные осям Jl и У, и крутящему моменту Mg, вызывающему кручение вокруг оси Z, совпадающей с касательной к оси бруса в месте сечения.

Для расчета прочности сооружения необходимо знать в каждом сечении бруса наибольшие значения изгибающих моментов, поперечных сил, нормальной силы и крутящего момента. Разрешение этой задачи при неподвижной нагрузке делается методом построения эпюр (см. Балки неразрезные и Балки простые), в случае подвижной нагрузки-методом линий влияния (см.). После того как одним из этих методов будут найдены в каждом сечении значения моментов, нормальных и поперечных сил, представляется возмолгным перейти собственно к расчету прочности, т. е. к определению внутренних напряжений и деформаций (см.)в брусе. Этому исследованию внутренних сил в брусе, возникающих при изгибе, сдвиге, сжатии и.ли растяжении и кручении, в курсах М. с. обычно предпосылают раздел, посвященный исследованию сечения, или так назыв. теорию сечения. Это исследование заключается в нахождении определенных ве-

личин, характеризующих сечение с геометрической стороны II называемых моментами и н е р ц и II (см.). Необходимость нахолоде-ння этих величин вызывается тем, что они входят в выражения, определяющие значения напряжений и деформаций при изгибе., сдвиге и кручении. В теории сечения подвергаются исследованию моменты инерции, центробежные моменты инерции и полярные моменты инерщпт, из к-рьгх в теории изгиба, Хгручения и сдвига находят применение в большинстве случаев т. п. г.тавиые центральные моменты инерции.

Как выше было указано, действрш внешних сил на элемент бруса в общем случае сводится к изгибу относительно двух осей, сдвигу параллельно двум осям, растяжению или сжатию и к^эучению, действующим на элемент одновременно. Для упрощения рассуждений обычно в М. с. сперва расчленяют все эти явления, рассматривают каледое из них в отдельности и лишь затем, изучив эти явления в чистом виде, переходят к рассмотрению комбинированных явлений, т. е. сочетаний нескольких одновременно действующих на э.темент бруса факторов. Эти чистые явления следующие: чистое растяжение или отрицательное растяжение - сжатие, т. е. случай, когда имеется только нормальная сила; чистый изгиб, т. е. случай, когда действие внешних сил на сечение сводится только к изгибающему моменту относительно одной из главных осей инерции сечения; чистый сдвиг, т. е. случай, когда на сечение действует только поперечная сила, и чистое кручение, т. е. случай, когда действие внешних сил на сечение сводится к крутящей паре. Чистые растяжение, сж;атие, изгиб и кручение м. б. реально осуществлены. Что же касается чистого сдвига, то рассмотрение его в качестве явления, возникающего в результате действия на сечение поперечной силы, м. б. сделано только путем нек-рой абстракции, так как поперечная сила молсет иметь место только при наличии переменного момента. Поэтому изучение сдвига в чистом виде в резу.11ьтате действия поперечной силы Q следует рассматривать как нек-рое условное расчленение двух явлений, т. е. сдвига и изгиба, по существу действующих всегда совместно. Явление чистого сдвига в элементарной частице тела м. б. все же представлено как результат одновременного действия растяжения и сжатия по двум взаимно перпендикулярным направлениям. Явление чистого сдвига имеет также место и при кручении.

В результате чистого растяжения или сжатия два смежных сечения бруса, оставаясь параллельными, взаимно удаляются или приближаются, причем это относительное линейное перемещение обратно нропорцио-нально т. наз. лсесткости при. растялгении-сжатии. При изгибе два смежных сечения поворачиваются одно относительно другого, причем угол относительного поворота обратно пропорционален жесткости при изгибе. В кривом брусе явление осложняется тем, что нормальная сила вызывает дополнительный поворот смежных сечений, а изгибающий момент их дополнительное сближение или удаление. Как сжатию или растя-

жению, так и изгибу соответствует лине й-иая деформация волокон, параллельных оси бруса. Соответственно этим деформациям в сечениях, норма-тьных к оси бруса, возникают внутренние силы-нормальные напряжетт (см.), которые уравновешивают действие нормальной силы на сечение. При растяжении-сжатии напряжения эти распределяются при отсутствии резких изменений в сечениях бруса равномерно по сечению, при изгибе же папрял^ения растут пропорционально расстоянию от той оси, относительно которой происходит изгиб. В случае резкого изменения сечения бруса напрян^ения распределяются по более сложному закону, п задача становится неразрешимой методами М. с. Величину напряжений находят, исходя из гипотезы плоских деформаций. Для брусьев малой кривизны предположению, что плоские сечения остаются плоскими и после деформации, соответствует и допуш;ение того, что нормальные напряжения изменяются по сечению по закону плоскости (закон Навье). В результате сдвига два смежных сечения перекашиваются одно относительно другого. Величина этого перекоса обратно пропорциональна т.н. жесткости сечения при сдвиге. Соответственно этому перекосу в сечении возникают тангенциальные напряжения. Эти напряжения распреде.71яются по сечению неравномерно. Закон их распределения из.тагается в теории изгиба. В некоторых случаях (напр. при расчете заклепок на срез, врубок на скальшание) распределение тангенциа.тьных напряжений чисто условно принимается равномерным.

При кручении бруса два смелсных сечения поворачиваются или закручиваются одно относительно другого вокруг оси бруса. Угол закручивания при кручении обратно пропорционален так паз. жесткости при кручении. Яв-тение кручения в курсах сопротивления . материалов рассматривается обычно только для бруса круглого сечения, в отношении к-рого можно считать, что плоские сечения остаются при малых деформациях плоскими и после закручивания бруса на определенный уго.71. Деформация кручения в этом предположении сводится к повороту одного сечения относительно другого вокруг оси бруса, т. е. к относительным сдвигам точек сечений; напряжения при кручении следо-вате.тьно являются напряжениями тангенциальными. Величина сдвига, а следоватсть-но и напряжения, при кручении бруса круглого сечения пропорциона.чьна расстоянию данной точки сечения от оси. Значение этого напряжения находят, исходя из условий равновесия сил внешних и внутренних, при-лолгенных к сечению. Прп кручении стержней некруглого сечения поперечные сечения стержней перестают быть плоскими. В отношении таких стержней элементарные методы М. с. не могут дать точного решения. Поэтому обычно курсы М. с. ограничиваются приведением д.тя ряда сечений готовых значений напряженш! и углов закручивания, полученных пли путем применения методов теории упругости или путем экспериментального исследования. Некоторые курсь! М. с. излагают исследование стеряней эл-

липтических и прямоугольных. К более уг-луб.летшым методам расчета, чел1 те, которыми обычно располагает М. с, приходится прибегать и при исследовапгп! тех напряжений, которые возникают в результате резких изменений сечений по длине бруса, подвергнутого кручению.

Помимо напряжений, возникающих в сечении в резу.тьтате действия на него совокупности сил, .лежащих вне сечения, в брусе возникают напряжения и от действия на элемент нагрузки, расположенно!! непосредственно в данном сечении. Напряжения, возникающие в результате Taicofi нагрузки, называются местными. Точное нахождение вел!!-чины этих напряяеп!1й не м. б. получено методами М. с, но в простейших случаях приближенное решение м. б. получено и эл( ментарным путем.

Исследование каясдого из чистых яБ.лений, т.е. чистого растяжения-сжатия, сдвига, изгиба и кручения, позволяет, пользуясь принципом независимости действия сил:, изучить и комбинированные, или сложные явления, т. е. сочетания двух или более чистых явлений. Из таких сложных явлений прежде всего излагается явление изгиба бруса системой сил, лежащих в плоскости оси бруса и парал.ле.льных одной из главных осей инерции сечения. Случай этот представляет собой сочетание действия на брус изгибающего момента и поперечно!! силы. К числу комбинированных явлений надо отнести и случай 1-сосого изгиба, т.е. изгиба, при к-ром вектор изгибаю1цего момента не совпадает с одной из главных осей !1нерции сечения. Случай этот может рассматриваться как совместное действие двух чистых !згибов относительно каждой пз главных oceit сечения. Более сложным является случай, к-рый имеет место при действии на сечение силы, параллельной оси бруса, но не проходящей через ц. т. сечения. Этот случай, называемый иногда в курсах М. с. неравномерным сжатием, а иногда общим случаем действия сил, приводится к совместному действию двух чистых изгибов и чистого растяжения-ся{:атия. Наконец в курсах М. с. !13,лагается и случай комбинированного изгиба ir 1сручен!тя. В тех случаях, вюгда в результате сложного сопроигвления бруса в его сечениях, нормальных к оси, возникают как нормальные, так и тангенциальные напряжен!1я, необходимо бывает для суждения о прочности подвергнет, исследованию и т. и. !<;осые напряжения. Это наименование дается напряжениям, имеющим место в площад1ч;ах, наклоненных под нек-рым углом к сечению, нормальному к оси бруса. Величины этих на-пряженпй меняются в зависимости от указанного уг.ла нахстона площадки. Максимальные и мннима,лы!ые значения косых норма.льнь!х и kociix тангенциа.льных напряжений носят название главных нормаль-пыхи главных тангенциальных напряжений. Для того чтобы судить по на11денным деформациям II напряжениям о необходимых размерах п1)ое1стируемого соору^кения или о запасе прочности в сооружении существующем,- необходимо знать, 1{;аким значениям напряжехшй илп деформаш1Й или сочетаниям нх соответствует появление в мате-

риале явлений, признаваемых недопустимыми. Для тел пластических этими недопустимыми явлениями будет появление остаточных деформаций, для тел хрупких-разрушение. В виду того что природа и механизм появления остаточных деформаций и механизм разрушения в реальных телах отличаются, с одной стороны, сложностью, а с другой, зависят в некоторой степени от обстоятельств, трудно поддающихся анали-тическ. учету, п}эиходится при определении прочности исходить из той или иной рабочей гипотезы прочности, наиболее близко отве-чающ й свойствам данного материала. Эти рабочие гипотезы носят название теорий прочности (см.).

Имея в своем распоряясении методы нахождения деформаций в любой точке оси, возможно определять также и перемещения в исследуемом брусе. При растяжении или сжатии эти перемещения будут результатом удлинения или укорочения соответствующего участка оси бруса и м. б. найдены в общем случае путем интегрирования выражения удлиненного элемента ds оси бруса. При кручении перемещение имеет угловой характер и измеряется углом закручивания но длине рассматриваемого участка. Этот угол закручивания м. б. найден как интеграл от выражения элементарного угла закручивания на длине элемента ds оси закручиваемого бруса. Перемещения при действии изгиба возникают в результате того, что ось бруса в деформированном состоянии в ка}кдой точке получает определенное изменение кривизны, в результате чего прямой напр. брус становится кривым. Очертание оси бруса в деформированием состоянии носит название у п-ругой линии. 1 еория изгиба доказывает, что в отноишнии бруса малой кривизны дополнительная кривизна в любой точке бруса прямо пропорциональна изгибающему моменту и обратно пропорциональна жесткости при изгибе. Нахождение ординат упругой линии следовательно сводится к чисто геометрич. задаче нахождения ординат кривой, форма к-рой определяется известным законом изменения кривизны, а положение в плоскости-заданными направлениями перемещения опорных точек. Направления этих перемещений определяются характером опорных закреплений. Задача нахождения ординат упругой линии значительно упрощается тем, что представляется возмож;ным (в виду того, что М. с. ограничивает свою задачу лишь случаями малых перемещений) приравнивать кривизну бруса, получающуюся в результате изгиба, второй производной от выражения прогиба бруса. Интегрирование производится отдельно на каждом участке бруса, имеющем свой закон изменения кривизны. Число произвольных постоянных, возникающих при нахождении значения у в процессе такого двукратного интегрирования, будет следовательно равняться удвоенному числу имеющихся участков. В таком виде соотношение между кри-в;тзной, выражаемой через изгибающий момент бруса и жесткость сечения, и ординатами упругой линии или прогибом носит название диференциального ур-ия упругой линии. Основываясь на этой диференциаль-

ной зависимости между моментом и прогибом, нахождение ординат прогиба можно делать аналитически, графически или гра-фо-аналитически. Апалитич. решение сводится к двукратному интегрированию выражения кривизны и определению произвольных постоянных интегрирования, исходя из условий опорных закреплений и т. и. условий на границах каждого участка, на к-ром кривизна имеет свой особый закон изменения.

Графич. и графо-аналитич. методы основаны на имеющей место определенной аналогии между изгибаюшими моментами, поперечными силами и нагрузкой, с одной стороны, и ординатами упругой линии, тангенсами углов наклона касательных к ней и кривизнами-с другой. Эта аналогия заключается в том, что значение поперечной си-лы.с одной стороны, и тангенсов углов наклона, с другой, являются соответственно первыми производными от значения моментов и прогибов, а значение нагрузки и значение кривизны-вторыми производными от тех же величин. На основании этой аналогии представляется возмолным тангенсы углов наклона балок находить как поперечные силы, а прогибы-как моменты от условной нагрузки, действующей на условное сооружение, причем за условную нагрузку принимается эпюра кривизны, за условное же сооружение берут такое, в котором имеется заделка там, где у действительного бруса- свободный конец, свободный конец-там, где у действительного бруса имеется заделка, а шарнир-там, где у действительного сооружения имеется шарнирная опора.

Все указанные выше разделы М. с. относились к системам, представляющим собой один брус или стержень. Комплексу этих разделов обычно дается название сопротивления материалов . Комплексу же разделов, трактующих о сооружениях, предста-. вляющих собой сочетание нескольких стержней, присваивают название статики сооружений . Такие сооруления м. б. подразделены на шарнирно-стержневые системы, или фермы (см.), и на сооружения с жесткими узлами, иначе рамы (см.). Рамы в большинстве случаев являются системами статически неопределимыми и рассматриваются в разделах, посвященных этой группе сооружений. Главную лее задачу статики сооружений в части, касающейся статически определимых систем, составляет расчет ферм. Расчет этих последних основан на замене действительного сооружения с жесткими узлами условной расчетной схемой, построенной в предположении наличия идеальных, т. е. работающих без трения, шарниров во всех узловых соединениях. Нагрузка в отношении такой схемы принимается приложенной в узлах системы. Нагрузку, приложенную вне узлов, раскладывают на составляющие, приложенные в узлах, и дополнительно учитывают местный изгиб того элемента, в пределах к-рого расположена нагрузка. Плоская статически определимая ферма, представляющая один жесткий диск, при общем числе узлов к должна иметь внутренних стержней w=2/c-3. Для статически определенного прикрепления к земле такого жесткого диска необходимо иметь еще три

опорных стержня. При таком числе стержней геометрически неизменяемая система представляет собой и статически определимую систему. При большем числе стержней система будет статически неопределимой. При меньшем числе система превращается в геометрически изменяемое сочетание стержней. Часть внутренних стержней м. б. заменена таким же числом соответственно расположенных дополнительных опорных стержней. Вследствие приложения нагрузки только в узлах фермы и предположения об идеальности шарниров в стержнях, составляющих ферму, в элементах будут иметь место только нормальные силы или усилия. Для нахождения этих усилий применяют графич., аналитич. и графо-аналитич. приемы. В случае неподвижной нагрузки графическое нахождение усилий в ферме производят путем построения диаграммы Кремона (см. Графическое определение усилии). Аналитическое определение усилий в фермах делается или методом сечений или методом вырезаний узлов (см. Фермы). В случае подвижной нагрузки для нахождения величины усилий в элементах фермы пользуются ин-флюентными линиями этих усилий. Построение этих пнфлюентных линий основывается на тех же методах сечения или вырезания узлов (см. Линии влияния).

Определение прогибов в шарнирно-стерл^-невых системах м. б. сделано методом упругих грузов (см. Графическое определение перемещений) или же применением основных теорем о перемещениях. Эти основные теоремы о перемещениях распространяются как на системы сплошные, так и сквозные и могут рассматриваться как обобщение начала возможных перемещений Лагранжа на упругое тело. В этом обобщенном виде теорема Лагранжа обнимает собой работу как внешних, так и внутренних сил системы. При этом за возможную систему перемещений для данной системы сил принимается такая, к-рая возникает в данном сооружении в результате упругой деформации его под действием любой другой воображаемой системы сил. Т. о. за виртуальные перемещения для внешних сил принимаются не бесконечно малые, а конечные, хотя и очень малые, перемещения, являющиеся результатом упругой деформации тела. Силы действительного и воображаемого состояния считаются приложенными к оси бруса в ее недеформи-рованном состоянии, что является допустимым постольку, поскольку пере.мещения дей-ствителыюго состояния являются относительно весьма малыми величинами по сравнению с общими размерами тела. Для нахож-денпя в действительном состоянии линейного или углового перемещения в направлении т-т точки m какого-нибудь сооруж;е-ния в воображаемом состоянии по этому па-правлению прикладывают к сооружению силу Р = 1, причем под силой Р здесь понимают как собственно силу, так и момент, если определяется угловое перемещение. Тогда из условия равенства нулю работы сил внешних и внутренних воображ;аемого состояния на пути внутренних и внеипп1х перемещений действительного состояния,для искомого перемещения получается для нахождения пе-

ремещения выражение, носящее название ф-лы Мора или Максвелла-Мора. Для нахождения относительных перемеп1ений в воображаемом cocTOjnnni прикладываются к системе групповые единичные нагрузки, т. е. нагрузки, состоящие из двух единичных сил или пар, направленных по искомому относительному П(ф,шещению. Для нахождения переметцений часто пользуются также теоремой Кастильяио. Н;.1х(}Ждение пер мещ:-ПИЙ, согласно этой теореме, дающей зависимость между величиной перемещения и потенциальной энергией упругой деформации системы, по существу не отличается от определения перемещения методом Мора.

Распространение начала возмолчных перемещений на упругое тело позволяет также установить нек-рые весьма важные положения, известные как теорема о взаимности работ (Бетти) и теорема о взаимности деформаций (Максвелла). Первая из этих теорем обнимает собой общий случай действия на сооружение последовательно двух произвольных систем или, как принято говорить, случай двух состояний одного и того же сооружения. Согласно теореме Бетти работа внешних сил первого из таких состояний на пути перемещенпй второго состояния равна работе внеиших си.т второго С0СТ0ЯШ1Я на пути перемещения первого (см. Взаимность перемещений). Теорема Максвелла мояет рассматриваться как частный случай теоремы Бетти, именно как тот, где и в первом и во втором состоянии к сооружению приложено по одной силе, причем силы nef)вого состояния и второго равны ме5кду собой (взаимность деформаций). Согласно этой теореме перемещение в первом состоянии по направлению силы второго состояния равно перемещению во втором состоянии по направлению силы первого состояния. Аналогичные соотношения м. б. выведены таюке и для случаев, когда воздействиями являются не силы, а перемещения.

Методы нахождения перемещений и вьште-указанные теоремы Бетти и Мора позволяют производить расчет не только систем статически определимых, но и статически неопределимых, т. е. систем, обладающих излишним числом связей внутренних или внешних против числа, необходимого для обеспечения геометрич. неизменяемости системы. При расчете таких сооружений необходимо для нахождения т. н. лишних неизвестных использовать в дополнение к ур-иям статич. равновесия также и ур-ия, вытекающие из рассмотрения картины деформации соору-н-сения, определяемой характеро-м избыточных связей. Как правило при расчете статически неопределимых систем вводят в рассмотрение т. п. основную систему. Эта система в общем случае получается пз изучаемой путем отбрасывания нек-рого числа существующих в системе связей и введения в систему нек-рого числа дополнительных связей. По направлению какдой из отброшенных связей прикладываются силы, причем под силами в данном случае понимают как собственно силы, так и моменты. По направлению же вновь введенных связей системе даются перемещения линейные или

угловые. Силы эти и перемещения принимаются за неизвестные, для нахождения к-рых составляют столько дополнительных ур-ий, сколько имеется неизвестных сил и перемещений вместе взятых. Если основная система получена из изучаемой путем отбрасывания п имеющихся связей и введения т новых дополнительных связей, то общее число неизвестных будет равно п+т. Для нахождения этих перемещений используют п условий равенства нулю перемещений но направлению неизвестных сил и m условий равенства нулю усилий по направлению m введенных дополнительных связей. По закону аддитивности воздействий каждое из указанных равных ну.лю перемещений по направлению неизвестных сил м. б. представлено как сумма перемещений от действия на основную систему^ нагрузки неизвестных сил и перемещений в отдельности. Также каждое равное нулю усилие по направлению вновь введенных связей м. б. представлено как сумма усилий от нагрузки, неизвестных сил и неизвестных перемещений. Ур-ия, составленные на основании этих соображений, носят название канонических ур-ий. Если основная система получается из изучаемой системы только путем отбрасывания связей без введения новых, то все неизвестные будут силами. Этот метод носит название м е-тода сил. Обычно при этом число отброшенных связей равняется числу лишних и избыточных связей системы. Полученная т. о. основная система носит название основной статически определимой систели.!. Если основная система получается из изучаемой только путем введения новых связей, то все неизвестные будут перемещениями. Такое решение носит название метода перемещений или деформаций. Наконец метод, при к-ром за неизвестные приняты как силы, так и перемещения, м. б. назван смешанным методом. В зависимости от конфигурации сооружения и характера нагрузки выбирают тот из методов решения, те из неизвестных и наконец те из методов решения системы ур-ий, которые в данном частном случае должны дать решение наиболее короткое и сопряженное с наименьшим накоплением арифметич. погрешностей. После того как путем разрешения вышеуказанной системы ур-ий определены все лишние неизвестные, .тюбые величины усилия пли перемещения в изучаемой системе м. б. вычис-лены по ф-.че, согласно принципу независимости действия сил, как сумма усилий или перемещения от каждой силы и.71и перемещения в отдельности. Ряд методов расчета статически неопределимых систем, как то: методы фокусов, угловых фокусов, но являются непосредственно частным случаем применения канонич. ур-ий, но находятся с этим методом в определенной косвенной связп.

К вводным или особым главам сопротйв-vicHHH материалов обычно относят разделы, посвященные неустойчивым формам равновесия и динамич. нагрузке. Из неустойчивых форм равновесия в М. с. обьгано ограничиваются рассмотрением продольного изгиба. Это явление заключается в том, что нри центральном сжатрш прямолинейного стержня при

значении сжимающих сил, превышающем нек-рую критич. величину, становятся теоретич. возможными, кроме формы равновесия с сохранением ирямолинейности оси стержня, также одна или несколько форм равновесия с изогнутой осью. Однако вероятность всех кроме одной теоретически возможных форм равновесия, в том числе и прямолинейной формы, равна нулю. При этом явления в брусе при сжимающих силах, превышающих критич. значение, имеют катастрофич. характер, даже если и не будет иметь места разрушение стержня, т. к. ничтожному возрастанию нагрузки будет соответствовать весьма большое воастание перемещений. Определение критич. грузов для стержней, загрунсенных по концам, дано еще Эйлером. Однако на практике к определению критич. нагрузок обычно не прибегают, а вводят при расчете сжатых стержней некоторый коэф. ослабления допускаемых напряжений. Таб-.пицы или кривые изменений этих коэф-тов нормируются соответствующими органами, причем при составлении таких норм руководствуются также и конструктивными соображениями. К вводным главам сопротивления материалов следует также отнести разделы, посвященные динамич. действию нагрузки. Эти отделы обычно заключают в себе рассмотрение напряжений в движущихся стержнях в результате действия сил инерции, а также рассмотрение явлений при ко-.лебании систем и ударном действии на систему нагрузки.

к особым главам статики сооружений обычно относят исследование сыпучих тел. В этом разделе дисциплины, подобно тому как в отношении твердых тел, принимается условная гипотеза идеальности свойств этого тела; при рассмотрении сыпучих тел действительные сыпучие тела заменяются сыпучими телами идеальными. В отношении такого идеального сыпучего тела предполагают, что силы сцепления между его частицами полностью отсутствуют и что размеры самих частиц являются величинами весьма малыми. Далее, при определении давления на подпорную стенку такого сыпучего тела предполагается, что эта подпорная стенка находится в состоянии предельного равновесия. Задача этим предположением сводится к рассмотрению равновесия призмы обрушения сыпучего тела в момент ее предельного равновесия. Для разрешения этой задачи дополнительно вводят гипотезу, что поверхность обрушения этой призмы есть плоскость. При этом ищут не действительную величину давления на стенку, а максимально при сде-.танных предположениях возможную. В более сложных случаях, напр. в случае ломаной стенки, приходится еще прибегать к ряду допстнительных предположений и допу-П1,ений, находящихся иногда в значительном противоречии с действите.пьными явлениями в сыпучих телах.

Лит.: II р о с к у р я к о в Л., Строит, механика, 4.1,7 изд., М.-Л., 1928, ч. 2, М.-Л., 1926; Велихов П. А., Теория инж. сооружений, вып. 1, М., 1924; Прокофьев И. П., Теорип coopv/кений, ч. 1-2, М., 1926-28; Т и м о ш е н к о С. П., Курс сопротивления .материалов, 6 изд., М.-Л., 1928; Ки1)ппчев в. Л., Сопротивление лтатериалов, ч. 1-2, М.-П., 1923; Дружинин С. И., Теории сопротивления материалов, ч. 1-2, П., 1923;

Руднев В. И., Строит, механика, М.-Л., 1928; Кирпичев в. Л., Основания графич. статики, 5 изд., М.-Л., 1924; Гвоздев А. А., Общий метод расчета статически неопределимых систем, М., 1927; Жемочкин Б. Н., Расчет рам методом угловых фокусов, М.-Л., 1929; его же, Расчет статически неопределимых систем. Способ угловых деформаций, М.-Л., 1928; Стрелецкий Н.С., К расчету сложных статически неопределимых систем, М., 1922; Г е л е р В., Жесткие рамы, пер. с нем., М., 1928; Тимошенко С. П., Курс статики сооружений, ч. 1, Л., 1926; Велихов П. А., Краткий курс строительной механики, М., 1927; Б е л е л ю б-с к и й Н. А., Строит, механика, СПБ, 1897; ф и л он е п к о-в о р о д и ч М. М., Основы теории работы упругих сил в плоских системах, М., 1925; Kirch-h of f R., Die Statilc d. Bauwerke, 2 Aufl., B. 1-2, Berlin, 1928; Strassner A., Berechnung statisch unbestimmter Systeme, B. 1, 2 Aufl., Berlin, 1929, B. 2, Berlin, 1921; F б p p I A., Vorlesungen uber teclini-sche Mechanik, B. 1, 8 Aufl., В.-Lpz., 1925, B. 2, 7 Aufl., В.-Lpz., 1926; Pirlet J., Compendium der Statik der Baukonstruktionen, B. 2, T. 1-2, В., 1921-23; Levy M., La statique graphique, partie 1, Paris, 1907, partie 2, Paris, 1913, partie 3, Paris, 1918, partie 4, Paris, 1888: M о h r 0., Abhandlungen auf dem Gehiete der technischen Mechanik, 3 Auflage, Berlin, 1928. H. Щапов.

МЕХАНИКА ТЕОРЕТИЧЕСКАЯ, учение о движении материальных тел. Если какое-либо тело с течением времени изменяет свое положение по отношению к какому-либо другому телу, называемому телом (системою) отсчета, то говорят, что первое тело находится в состоянии движения по отношению ко второму, в отличие от состояния покоя, когда относительное положение тел остается неизменным. Т. о. понятие движения содержит в себе понятие пространства, времени, перемещающегося объекта и системы отсчета. Понятия пространства и времени, являясь предметами исследования философии, обычно предполагаются в М. т. данными. Что касается перемещающегося объекта, то в действительности он не всегда является материальным телом, напр. перемещающаяся тень, смещение силовых линий в силовом поле и т. п. Движение материальных тел называется движением корпускулярным. М. т. занимается изучением только корпускулярных движений. Обычно изучение движения материальных тел начинают с изучения движения материальной точки. Под материальной точкой подразумевают в М, т. тело произвольной величины при наличии по крайней мере одной из следующих предпосылок: когда все линейные размеры тела ничтожно малы по сравнению с расстояниями от рассматриваемого тела до других тел, играющих роль в данной проблеме, или когда вращение тела не принимается во внимание, а рассматривается лишь движение центра массы (центра тяжести)тела (см. Центр тяжести). Так напр., рассматривая движение земного шара вокруг солнца, можно землю принимать за материальную точку, чего нельзя делать, рассматривая движение земли вокруг ее оси. Установив законы движения материальной точки, выводят затем из них законы движения системы отдельных материальных точек и сплошных материальных сред (континуумов). Допустимость последнего перехода в йоследнее время однако подвергается сомнению. Если все точки данной совокупности, или системы материальных точек, сохраняют свои взаимные расстояния неизменными, то система назьшается твердой, в противоположном слу-

Т. Э. т. XIII.

чае-нетвердой. В частности, если материальные точки системы заполняют определенный объем, то такая система точек называется т е л о м-твердым или нетвердым в зависимости от вышеуказанных признаков. В качестве системы отсчета обычно берут твердое тело, с к-рым неподвижно связаны три взаимно перпендикулярные пересекающиеся в одной точке прямые Ох, Оу, 0.г, называемые осями координат. На практике телом отсчета чаще всего служит земля или какое-либо твердое тело, неподвижно с ней связанное.

Из предшествующего следует, что понятия движения и покоя суть понятия относительные и что, поскольку все известные нам системы отсчета сами находятся в движении по отношению к другим телам отсчета, нельзя говорить ни об абсолютном движении ни об абсолютном покое их. Если бы хотя одно тело находилось в состоянии абсолютного покоя, то можно было бы судить как об абсолютном, так и об относительном характере движения всех прочих тел. В 19 в. эфир- носитель световых и электромагнитных явлений-считался, за исключением малых колебаний его, абсолютно неподвижным. Этим самым создавалась такая система отсчета, по отношению к к-рой всякое движение могло быть названо движением абсолютным, а покой-абсолютным покоем. Эта точка зрения в корне опровергается современной теорией относительности, которая в числе прочих своих заключений приходит к выводу, что даже в области электромагнитных явлений не представляется возможным отличить абсолютный покой от равномерного поступательного движения системы. В связи с коренной ревизией понятий пространства и времени, совершенной теорией относительности Эйнштейна, М. т., основы которой были положены Ньютоном и которая называется классической, рассматривается в настоящее время как частный случай более общей системы М. т., называемой релятивистской. Выводы классич. М. т. справедливы лишь как первые приближения для корпускулярных движений, происходящих со скоростями, ничтожно малыми по сравнению со скоростью света. В дальнейшем здесь излагаются основы лишь классич. М. т.

Обычно М. т. разделяют на кинематику, статику и динамику. В кинематике рассматривают только геометрич. свойства движения, не приншлая во внимание действующие силы. В статике рассматривают те условия, которым должны удовлетворять данные силы, чтобы система, к которой они приложены, находилась в покое. В д и-н а м и к е изучается зависимость между силами и соответствующими движениями системы материальных точек. Статику и динамику объединяют часто в один отдел- кинетику. Часто в М. т. выделяют особый отдел, т. н. геометрию масс, изучающую свойства распределения массы системы в пространстве; сюда относятся связанные с центром масс, с моментами инерции (см.) и т, п. вопросы.

Кинематика, рассматривает законы движения тел независимо от действующих сил.

Движение какой-либо совокупности или системы материальных точек, в частности

движение твердого тела, определяется движением всех точек, составляющих систему, вследствие чего является необходимым исследовать сначала свойства движения отдельной точки и затем лишь свойства движения какой-либо совокупности их.

Пусть имеется точка А, движущаяся по отношению к нек-рой системе отсчета, состоящей из 3 взаимно перпендикулярных осей координат Ох, Оу, Oz, имеющих начало в точке О. Каждое положение точки А по отношению к заданной системе координат определяется некоторой тройкой отрезков X, у, Z, взятых со знаками (-f) или (-) или, что равносильно, нек-рым радиусом-вектором г, имеющим начало в О, а конец в рассматриваемом положении точки А, причем

г = ГГх, (1)

где Гх-единичный вектор (орт), определяющий направление OA, а г-численное значение этого отрезка (модуль). При движ;ении точки А координаты &е х, у, z с течением времени изменяются, так что для данного движения имеют место три функциональные зависимости между координатами точки А и временем t:

х-hit), у = Ш, z = U{t). (2)

Последние ур-ия, характеризующие данное движение точки А, называются уравнениями двиимения. Т. к. при движении точки А радиус-вектор г изменяется с течением времени, то г-также нек-рая ф-ия t: r = r(t) = xi+yj-{-zk, (3)

где i,J, и-единичные векторы, определяющие направление осей координат, причем последнее векторное ур-ие вполне заменяет собою три ур-ия движения (2). Совокупность всех положений точки в пространстве при данном ее движении называется траекторией. Если траектория-плоская кривая, то и движение называется плоским; в этом случае для определения движения точки достаточно двух осей координат-Ох и Оу, взятых в плоскости движения. Если траектория представляет собой прямую линию, то движение называется прямолинейным; в последнем случае для определения движения точки достаточно одной оси координат Ох, совпадающей с прямолинейной траекториейточки. Прямолинейность или криволинейность движения суть также понятия относительные, зависящие от состояния, в котором пребывает сама система отсчета. На траектории следует различать две особые точки; начало отсчета 0 длины s кривой (где s=0) и начальное положение А^ точки А, т. е. то ее положение, при к-ром начался отсчет времени (t = 0). В целях упрощения часто берут однако начало отсчета длины Oq совпадающим с начальным положением Aff точки (фиг. 1), так что OqAqO. Каждому определенному моменту t соответствует определенное значение величины 5 = о^1>так что S есть нек-рая ф-ия от t:

s-fit). (4)

Фиг. 1.

Если на оси асбцисс отложить отрезки, пропорциональные истекшим промежуткам времени f, а по оси ординат отрезки, пропорциональные S, то геометрическое место получившихся точек-некоторая кривая, которая называется графиком пройденного пути (фиг. 2). Пусть в момент точка А находилась от Oq на расстоянии OqAi=Si, считаемом по длине кривой,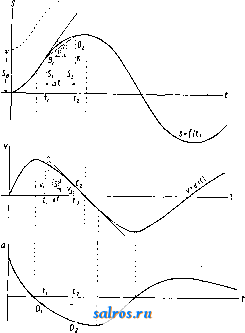

Фиг. 2, 3, 4.

а в некоторый последующий момент на расстоянии 02 = s, так что за промежуток времени fа - = точка прошла по своей траектории путь s - SiAs. Среднею линейною, или скалярною, скоростью г?ср, точки А за промежуток времени М называется частное от деления As на At, т. ч.

ср. = (5)

Если обозначить на графике пути точки, соответствующие положениям А- и А^, через Bi и В2, ТО Vcp, равняется тангенсу угла, образуемого отрезком В^В^ с положительным направлением оси t:

ср.

Линейною, или скалярною, скоростью v в данный момент называется предел отношения -, когда At стремится к О, т. е. v равняется производной s по переменному t:

Очевидно в общем случае v есть также некоторая ф-ия от t:

vcp{t). (8)

Из ур-ия (7) нетрудно видеть, что на графике пути

v = tga, (9)

где а есть угол, образованный касательной, проведенной к кривой в соответствующей точке, и положительным направлением оси t. Если способом, аналогичным вышеприведенному, построим кривую, выражающую функциональную зависимость (8), то получим т. паз. график скорости (фиг. 3). Интегрируя ур-ие (7), получаем:

s=fvdt + C=((p(t)dt + C, (10)

откуда также следует, что путь \s\\, пройденный точкой за промежуток времени от *1 до *2.

vdt=j<p{t)dt. (11)

tl h

Так как выражение, стоящее в правой части ур-ия (10), представляет собой на фиг. 3 площадь, ограниченную ординатами, проходящими через точки ti и t2, частью CCz кривой и осью абсцисс, то эта площадь и равняется численно пути \s\l. Из ур-ия (9) не трудно также видеть, что экстремальным точкам графика пути соответствуют точки пересечения графика скорости с осью t, а точкам перегиба первой кривой соответствуют экстремальные точки второй. Если в частности v = Const = F, то такое движение назьшается равномерным. В последнем случае имеем из ур-ия (10):

s = Ff + C. (13)

Если, при t = tl, s = Si, то, т. к. C=Si- Vt, имеем:

s=Vit-ti) + Si. (12)

Очевидно в этом случае график скорости будет представлен прямой, параллельной оси t, а график пути-прямой, наклоненной под углом а к оси t (фиг. 5), так что

tga=F. (13)

Пусть в нек-рый момент t движущаяся точка находилась в положении А, определяемом

по отношению к данной системе от- счета радиусом-вектором г, а в не--(который последующий момент t=t + +Af-в положении А', определяемом радиусом-вектором г'= = i*+A *. Среднею скоростью v. точки за промежуток времени At назьшается выражение

ср.-% (14)

Истинною скоростью V точки в момент t назьшается предел отношения (14) при At->0, т. е. производная вектора по времени t:

т. к. направление Аг в предельном положении совпадает с направлением касательной, проведенной к траектории в рассматриваемом положении точки, то направление V совпадает с направлением этой касательной; т. о. единичный вектор определяет также и направление касательной так что

Фиг. 5.

(15)

т. к. далее г = гг, то из (15) имеем:

~dt i dt

(IV)

T. o. вектор скорости м. б. представлен как сумма двух векторов:

(18)

v =r

(19)

причем первый вектор имеет направление,.

определяемое г^, а второй - вектором,

т. е. вектором, перпендикулярньпи к первому. Скорость Vr называется радиальной скоростью, а скорость v - трансверсальной, или поперечной, скоростью. Так как

(20)

где q)-угол поворота г около О, а Pi-единичный вектор, перпендикулярный г^, то

Vp = rPi.

(21)

Абсолютные значения этих скоростей очевидно следующие:

(22) (23)

Ж' d<p dt

откуда имеем также:

Т. к. параметры г и q) суть полярные координаты точки А (см. Координаты), то (24) представляет собою выражение скорости в полярных координатах. Если в частности точка А перемещается в пространстве так, что = Const, т. е. если А перемещается по прямой, проходящей через О, то, так как в

этом случае = О, из ур-ий (17-19) имеем:

(17)

dr dt

(17 )

Величина г играет в этом случае ту же роль, что и величина s в ф-ле (7), и следовательно формулы (10), (11) и (12) применимы и для прямолинейного движения с соответствующей заменой длины кривой s длиною прямолинейного отрезка г. Если же, наоборот, г= Const, то очевидно, что точка движется по шаровой поверхности. В этом случае

d<p I

(17 )

p~ dt dt В частности точка может перемещаться по кругу. Пусть в этом случае точка переместилась за промежуток времени At по дуге А9?, длина которой As. Если Ад? выражена в радианах, а г-радиус окружности, то

очевидно As = г А(р. Частное называется

среднею угловою скоростью (о^р. вращения точки:

Предел (о^р. при вой скоростью в момент t:

lim

О называется у г л о-вращения со точки

(г:)=

d<p

AtO\AtJ df

Т. О. (17 ) м. б. в рассматриваемом случае представлено епе в следующем виде:

г; = г О). (18)

Угловая скорость м. б. представлена вектором <о, проведенным из центра вращения перпендикулярно плоскости движения в такую сторону, чтобы наблюдатель, помещенный вдоль вектора, видел вращение точки происходящим по часовой стрелке. Если за промежуток времени At угловая скорость

изменилась на Асо, то частное - называется угловым ускорением Предел этого отнощения

средним точки: в,

при Af -> О называется угловым ускорением 6 в момент t:

б lim (\

М^О\и) dt Если в = Const, то движение называется равнопеременно вращательным, если же о)= Const, то движение называется равномерно вращательным.

Рассмотрим движение проекций точки А по трем взаимно перпендикулярным осям координат Ох, Оу, Oz. На основании (17 ) скорости этих точек при их движении

dx dy dz по соответствующим осям будут л , ,

С другой стороны, модули проекций скорости V на эти оси на основании (7):

, ds

\VJ = V cos а = cos а

dt de

= v COS )S = cos /5

Wl = V COS Y = COS у

(25)

(26)

где a, p, у-углы, образованные вектором v с положительными направлениями осей координат; т. к. ds cos а = dx, ds cos = dy, ds cosy = d2, TO из (18) имеем:

dx dt dv 2! dt

i ~dt ,

T. e. скорости проекций точки A на три оси координат равняются соответствующим проекциям скорости на эти же оси. Эти проекции скорости называются ее компонентами по рассматриваемым осям. При условии ортогональности осей имеем:

Зная ур-ия движения (2), можно ф-лы (26) и (26) написать еще и так:

=ту, Ууту, vz-m);

Моментом скорости v по отношению к некоторой точке С называется вектор, модуль к-рого равняется произведению v на длину d перпендикуляра, опущенного из С на линию действия V, а направление определяется

направлением перпендикуляра, восставленного к плоскости й , образованной v и С,в такую сторону, чтобы наблюдатель, помещенный вдоль него в точке С, видел v нанравлен-ным по часовой стрелке (фиг. 6). Т.к. длина перпендикуляра d, или и лечо, равняется d!=rsina, где а-угол между v и г^, то, обозначая момент скорости через Ж, имеем: М V d = V - г sin а

и

M = [vr,-\. (27)

Помещая начало отсчета О в точке С, имеем Гс = - г, где г = С А, и следовательно

М = [г- V]. (27)

Рассмотрим площадь Аа, сметаемую подвижным радиусом-вектором г за промежуток времени At до положения его * , так

что .4- (г, г') = А(р. Предел отношения нри

At-0 называетсясекториальной скоростью V точки; т. о.

Секториальная скорость м. б. представлена в виде вектора v, проведенного перпендикулярно JK плоскости, проходящей через г и г', где г'-последующий во времени радиус-вектор, бесконечно близкий к причем обычно направление v выбирают так, чтобы наблюдатель, помещенный вдоль v в начале отсчета О, видел вращение г происходящим по часовой стрелке. Так как

da==lrd(p = llds, (29)

где ds-длина элемента дуги, а I-длина перпендикуляра, опущенного из О на ds то, принимая во внимание (28) и (23), имеем:

df 2 df 2

= 2dt-=2--

(30)

Т. к., с другой стороны, da \ \\г dr\ то

- 1

принимая

(31)

во внимание

и следовательно, (27), получаем:

Ъ> = М, (32)

т.е.момент скорости v относительно нек-рого центра равен удвоенной секториальной скорости движущ! йся точки относительно того же центра. Если отложить от одной и той же точки векторы скорости движущейся точки нри различных ее положениях, то геометрич. MtCTo концов этих векторов образует кривую, называемую годографом скорости (см.).

Пусть за промежуток времени At линейная скорость изменилась на величину Аг;. Средним линейным, или скалярным, ускорением а^ называется част-

ное , так что

acp.-rt- (33)

Линейным, или скалярным, ускорен и е м о точки А в момент t называется предел отношения (33) при At-*О, т. е. производная V по времени t: