• Что такое фактурная штукатурка
• Выбираем сухие строительные смеси
• Преимущества напряженного железобетона
• Что влияет на выбор кровельного материала
• В чем преимущество пробковых полов

шм ~ 57.3t<i

при перемрнном отношении угловых скоростей, причем примем, что диаграмма изменения о) по времени имеет вид синусоиды, а соответствующее изменение со по времени дает диаграмму из ряда наклонных линий, как указано на фиг. 21. Расположим диаграммы (а>1, f) и (cog, t) так, чтобы их начало координат совпадало с геометрич. центром вращения оси ОгиОх-Ма-спггабы для диаграмм выбираем одинаковыми: 1 jvtjn-тек. по оси абсцисс и 1 мм-а ск.- по оси ординат. Проектируя ординаты, соответствующие одному и тому же моменту времени =тж, на оси ординат и соединяя полученные точ-ки, мы получим на линии

OjOg точку пересечения Р, т. к. из основного ур-ия мы будем иметь:

из подобия же треугольников OiWPigH О2НР13ПОЛУЧИМ:

О1Р13 OTW тУа Юг

На фиг. 21 построены этим методом точки Pjg nPg, причем точка Pi3 слуядат полюсом для момента времени ti=TXi и для момента времени <з=тжз благодаря симметрии диаграмм (coj, t)vi{(02, t). Точки плоскостей I л II, совпадающие в рассматриваемый момент в точке Pi на линии О1О2, находились за tl ск. до этого момента в точках Р{ и Pi. Эти точки м. б. найдены, во-первых, потому, что они лежат на дугах, описанных из Oi и О2 радиусами: OiPj и О2Р1, а во-вторых, потому, что углы, образуемые

линиями OiPi и OgPi с линией центров 002, пропорциональны площадям f[ я Ц, взятым над абсциссами х' и х' на диаграммах {(Oi,t) и {(02,t). На основании ур-ия: dip

= 1П

можем определить величину угла

9?= J (odt, о

считая, что угол, соответствующий f = О, тоже равен нулю; в нашем случае

<р{=-ах J ijidx orfi радиан,

Положение точки Р на линии OiOgnpn t = О в нашем случае не м. б. построено, так ка: при этом 1 = 2 = 0; поэтому можно применить приближенное построение, заключающееся в том, что полученные полоиды PiPi яР Р'1 продо.тжают до пересечения с ли-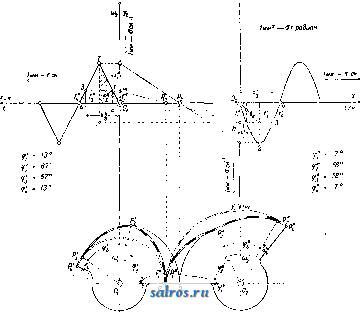

Фиг. 21-22.

1= аг J y2dx = orf

Вводя множитель 57,3, мы мож;ем определить углы в градусах. Аналогично указанному определены на фиг. 22 радиусы и углы точек (Р2, Рр и (Р^, Pg) и построено геометрическое место полюсов Р в относите.льном движшии. Эти кривые носят названле полоид пли центроид.

нией О1О2 в одной и той же точке Р^, причем касательная, проведенная к одной полоиде в точке Ро, д. б. касательной и к другой полоиде в той же точке. Основным свойством полоид является то обстоятельство, что движение одной полоиды по другой совершается без скольжения, а это свойство ставит требование, чтобы длина полоиды РоР^ была равна длине полоиды PqPI. Полученные полоиды в большинстве случаев не м. б. неносредственно использованы для передачи вращательного движения между параллельными осями. Чтобы создать передачу конструктивно правильной формы, необходимо снабдить полоиды зубцами так же, как это делается у обыкновенных цилиндрич. зубчатых колес (см.). В нашем первом примере ПО.ТОИДЫ получились в виде двух разомкнутых кривых, совершающих колебательное движение относительно центров валов Oi и Оз. Второй пример, указанный на фиг. 23 и 24, дает замкнутые полоиды, приспособленные для вращения в одном и том же направлении. На фиг. 24 показаны также зубцы, профиль которых получен методом циклич. зацеплений. Зубчатые колеса этого вида носят в М. п. название некруглые колеса .

В практике современного машиностроения большое распространение получили так паз. планетные передачи , вытесняя громоздкие ременные или обыкновенные зубчатые передачи. Схема такой планетной передачи простейшего типа дана на фиг. 25. Шестерня 1, соединенная намертво с ва.лом, делающим большое число оборотов,

т. о. т. XIII.

сцепляется с зубчатым колесом 2, а это колесо катится по зубчатому венцу 3. Ось зубчатого колеса 2 укреплена на шайбе 4,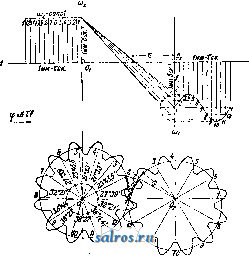

Фиг. 23-24.

посаженной намертво на приводной вал, де-лаюший уменьн1енное (редуцированное) число оборотов, и поэтому эти приборы носят название редукторов , хотя при помощи той же конструкции можно медленное вращение превратить в быстрое. П|.)едположим, что угловая скорость шестерни 1 нам дана, а также известны радиусы всех зубчатых колес. Обозначим точку соприкосновения первой шестерни с зубчатым колесом 2 буквой А, ось зубчатого колеса 2 буквой В, а точку соприкосновения зубчатого колеса 2 с зубчатым венцом буквой С. Скоростьточки /1 Vj= Qico представим на фиг. 26 от-резкомА^ лш, затем соединим топку А' с точками О и С. Распределение скоростей на радиусе будет давать треугольник О А А', Si распределение скоростей на диаметре зубчатого колеса 2 дает тр-к ААС, причем точка С скорости не имеет, являясь в данный момент полюсом мгновенного вращения при качении колеса 2 внутри венца 3. Скорость точки В пропорпиональна отрезку ВВ, а этот отрезок равен половине Отрезка АА, т. к..точка В делит сторону АС треугольника пополам, а сам отрезок ВВнаправлен параллельно линии АА. Поэтому

но точка В соединена намертво с шайбой 4, а потому угловая скорость этой шайбы найдется из ур-ия:

Следовательно передаточное число

со, 2,61 + Pi)

Соединим точку В' с точкой О. Полученный треугольникОББдает распределение скоростей на радиусе шайбы 4. Точка К, взятая на шайбе на расстоянии от оси вращения, имеет скорость ?fc=eift)2 и м. б. представлена отрезком 1{К', а потому передаточное число е м. б. определено также из соотношения:

6,0)2 £Я ggi в! ! VA AAi

Если дано передаточное число ей радиус Pi, то величина радиуса следовательно и размеры венца, м. б. найдены по ф-ле: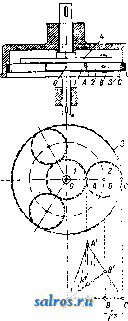

Фиг. 25-26.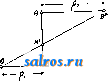

или простым построением, указанным на фиг. 27. Отложим по горизонтальному направлению радиус Qi и проведем к нему перпендикуляр через точку А; на этом перпендикуляре отложим выбранный отр^езок

- jji

АК и вычисленную величину АН = :

проводя затем через точки О я К' наклонную линию, а через точку Н параллель радиусу мы найдем величину 2 в виде отрезка Б J3. Рассмотренная система редуктора дает небольшие конст-руктивн. размеры толь- Фиг. 27.

ко при уменьшении числа оборотов не больше, чем в восемь раз. Если требуется большое уменьшение угловой скорости, то помещают один редуктор за другим (в одном кожухе), причем дают в одном редукторе уменьшение в четыре раза в другом редукторе в пять раз. В результате работы сдвоенного редуктора мы получим уменьшение скорости в 20 раз. Общий вид двойного редуктора системы Гень-шау дан на фиг. 28.

Перейдем теперь к рассмотрению траекторий, описываемых различными точками какой-нибудь системы, и к определению их радиусов кривизны. Для разрешения этой задачи мы будем пользоваться, как основным приемом исследования, методом проф. Гартмана, применяемым с успехом в тех случаях, когда полюс мгновенного вращения легко получить в пределах чертежа; во всех других случаях решение можно найти методом нормальных ускорений. Рассмотрим наиболее простой случай: круг катится без скольжения но прямой линии; Т1)ебуется определить траекторию одной из точек окружности и построить для различных точек, взятых в плоскости круга, радиусы кривизны траекторий этих точек. Возьмем круг некоторого определенного диа-

метра АР= d мм и развернем его окружность, равную Tzd мм, в прямую линию KL (фигура 29). Разделим эту длину на 24 равные части и перенесем эти деления

Фиг. 28.

на прямую линию NN, проведенную через центр круга О параллельно линии KL. Разделим также окружность круга на 24 равные части и проведем к точкам деления хгрды из точки касания Р круга с прямой KL. Кривая, описьгеаемая точкой А, взятой на окружности, называется циклоидой им. б. построена по точкам, получаемым при помоши засечек, напр. точка циклоиды Н получается засечкой радиусом 1Г5 из точки и засечкой отрезком Н5, равным хорде Ь Р. Найдем центр кривизны циклоиды для положения точки А на вертикальном диаметре АР. Предположим, что круг катится по прямой KL со скоростью Vo-**/<-Представим на фиг. 29 эту скорость центра круга отрезком 00, равным радиусу круга; следовательно распределение скоростей на вертикальном диаметре АР можно дать тр-ком скоростей РА А', проводя линрпо РА через точку О'. Определение центра кривизны (точка F) сводится, по мысли проф. Гартмапа, к построению треугольника скоростей для радиуса кривизны FA по двум отрезкам: первый отрезок соответствует скорости точки А и принят на

фиг. 30 равным AAi, а второй отрезок соответствует (в том же масштабе) скорости другой точки того же радиуса кривизны. На фиг. 30 второй точкой выбрана точка В и соответствующий отрезок

взят равным ВВ. Проведем линию А'В' и продолжим ее до пересечения с линией АВ. Точка пересечения, отмеченная буквой С, даст искомый центр кривизны. В рассматриваемом нами движении круга по прямой точку В должна заменить точка радиуса кривизны, совпадающая в данный момент с П0.Г1ЮС0М мгновенного вращения Р, а скорость Vs будет равна скорости центра круга Io, т. к. с этой скоростью происходит смена точек, в к-рых круг касается прямой. На фиг. 29 отложен отрезок PU, равный отрезку 00, и через точки А' и U проведена прямая, пересекающая направление радиуса кривизны в точке F - искомом центре кривизны. По построению отрезок А А' вдвое больше отрезка РСГ, а потому радиус кривизны AF вдвое больше диаметра круга АР. Построение радиуса кривизны для любой точки циклоиды, напр. для точки Н, м. б, заменено построением радиуса кривизны для точки II, к-рая взята на той же центральной окружности,причем линия НН проведена параллельно линии KL. В точке И' скорость м, б, представлена отрезком В'П , равньпм хорде П'Р. Проведем через точку Р прямую, перпендикулярную к линии П'Р, и спроектируем на эту прямую отрезок Р17. Полученный отрезок PR пропорционален скорости смены точек касания в направлении перпендикулярном к радиусу кривизны, а поэтому достаточно провести прямую через точки Н а R, чтобы на пересечении этой прямой с продолжением линии Н'Р получить центр кривизны-точку F. Тр-к PRU подобен тр-ку РНА и вдвое его

меньше, а потому ПН = Н'Р = 2 PR, следовательно, радиус кривизны HF =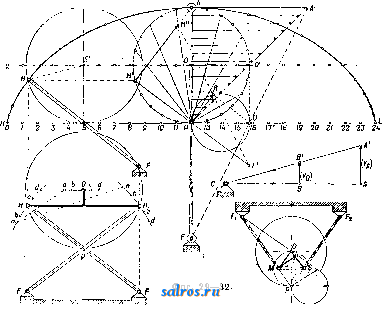

= 2 Н'Р'. Это равенство выражает известное из математики положение, что радиус кривизны циклоиды равен удвоенной

нормали. Этим свойством циклоиды можно Воспользоваться, чтобы создать целый ряд новых механизмов, обладающих той особенностью, что одна из точек этих механизмов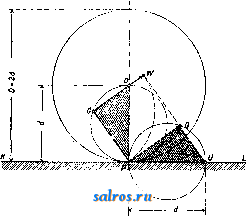

Фиг. 33.

при его движении описывает на значительном протяжении почти прямую линию.

На фиг. 31 мы имеем механизм, состоящий из двух равных стержней, связанных шарнирно с опорой и друг с другом при по-моши траверсы. Точка О этой траверсы занимает последовательно положения а, Ь, с и d, соответствующие перемещениям точек Н и J?i. Расположение этой точки О соответствует центру круга, проведенного через точки Р, Н и Hi. Нз чертежа видно, что траектория, описываемая точкой О, почти прямая линия. На фиг. 32 дано построение радиуса кривизны траектории точки М внутри круга, описанного на радиусе ОР как на диаметре. Построение но идее ничем не отличается от построения радиуса кривизны точек циклоиды, но центр кривизны Fx перешел в этом случае по отношению к полюсу Р на ту же сторону, где расположена точка М. Взяв симметрично расположенную точку и построив для нее центр кри-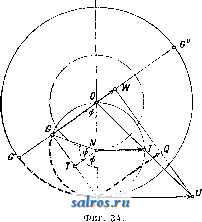

визны F, мы получим меха1П13м, известный в М. п. под названием механизм Роберта;.

На фиг. 33 дано построение радиуса кривизны траектории точки G, взятой на окру ле-

ности PGO, проходящей через полюс Р и центр О катящегося круга. Скорость точки

G, в масштабе jS= представлена отрезком GW равным отрезку GP. Построив окружность на отрезке Рй = ОР и проводя линию PQ под прямым УГ.110М к линии PG, мы получим отрезок PQ, необходимый пи предыдущему для построения радиуса кривизны траектории точки G. Но тр-к PGO равен тр-ку PQU, а потому отрезок GTF равен отрезку PQ; следовательно линия WQ не может пересечь линию GP, а потому радиус траектории точки G равен бесконечности, а сама точка G двигается по прямой, совпадающей с линией GO; это движение происходит лишь в течение бесконечно малого времени. Траектория точки G получает в этот мо- мент перегиб. Т. к. траектория любой точки, взятой на окружности PGO, обладает указанным свойством, то круг PGOP носит в М. п. название круга перегибов или поворотного круга . Изменим условия движения и рассмотрим случай, когда в неподвижном круге радиуса ОР (фиг. 34) катится без схсольжения круг с диаметром 1авным

С^.---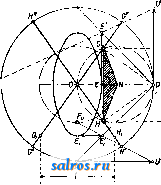

Фиг. 35.

ОР. Предположим, согласно предыдущему примеру, что скорость центра N катящегося круга т-ка представлена на чертеже отрезком JVJ. Соединив центр О большого круга с точкой I и продолжив эту прямую до пересечения с касательной, проведенной к обеим окружностям в полюсе мгновенного враще-нияР, мы получим отрезок Р[7, пропорциональный скорости смены полюсов. Так как PJJ = Р0, то построение радиуса кривизны траектории точки О, лежащей на катящейся окружности, приводит нас к выводу, что и в этом случае центр кривизны .лежит в бесконечности, а точка описывает прямую .линию GG (фиг. .34). На фиг. 35 проведены под произвольным углом два диаметра GG иНН ; по этим линиям двигаются нолзуш-ки Н и G, связанные друг с другом траверсой, длиной в1 м. Найдем радиус кривизны траектории, описываемой точкой Е, лежащей на середине траверсы HG. Скорость точки Е представлена отрезком ЕЕ, равным расстоянию точки Е до полюса мгновенного вращения Р. Проводя линию UE до пересечения с линией РЕ, мы получим в точке Fi искомый центр кривизны. Тем же

приемом определен на фиг. 35 центр кривизны Fji для расположения траверсы О^Н^, причем точка Е заняла положение Е^ на вертикальном диаметре. Путь точки Е при качении малого круга внутри больпюго будет представлен, как известно, эллипсом, и определенные выше радиусы кривизны позволяют легко установить очертания этого эллипса. Только что изложенный метод проф. Гартмапа не требовал знания закона изменения скоростей, а потому ускорение движущихся точек могло бьггь какой угодно величины.

При определении радиуса кривизны методом нормальных ускорений наиболее простые резу.71ьтаты получаются в том случае,

Vavm/ch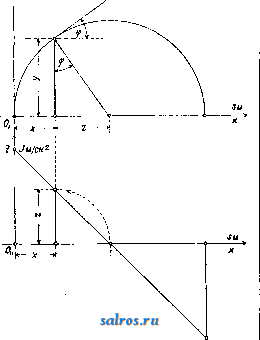

Фиг. 36 и 37.

когда основное движение в системе принято как равномерное движение. Так, скорость Vy центра круга N, катящегося без скольжения внутри другого круга, будем считать постоянной величиной, следовательно угловая скорость относительно центра Р мгновенного вращения о)/.= Const. Диаграмма скорости точки G (фиг. 34) по диаметру GG , имеет вид полуокружности GPG\ так как в любом положении точки G ее скорость, в

масштабе Р= пропорциональна отрезку

PG=GW. Диаграмма ускорений точки G найдется по диаграмтухе (vg, s), на основании построения (фмг. 36) по ф-ле dv

ds а dx где Z-отрезок, пропорциональный ускорению в рассматриваемой точке пути. В мертвых точках субнормаль z равна радиусу круга, а потому диаграмма ускорений точки G по пути S представляет прямую линию, наклоненную к оси абсцисс под углом 45° (фиг. 36 и37). Зависимость нормального

dy 0

ускорения точки А в криволинейном движении от радиуса кривизны д траектории этой точки и ее скорости г; дается, как известно, ф-лой

Применим эту ф-лу к движению по эллипсу точки Е (фиг. 35). Если масштаб чертежа а м в1 мм, а масштаб скоростей, по предыдущему, принят Р м/ск в 1 мм, то

= ~ Z

Построение отрезка z дано на фиг. 38, где тр-к EFjE взят равным такому же тр-ку на фиг. 35, Проведем линию Е'Е под прямым углом к линии EFi и точку пересечения линии Е'Е с продолжением линии EFi обозначим буквою Е . Т. к.

то ЕЕ ==Ze.

Следовательно, зная величину нормального ускорения и представив это ускорение

в масштабе у = ~ м/ск в 1 мм отрезком ЕЕ ,

мы можем получить радиус кривизны траектории точки Е, если отложим под прямым углом к направлению нормального ускорения отрезок ЕЕ, дающий в масштабе j8 м/ск в 1 мм скорость точки Е. Соединив точки. Е я Е' VL проводя перпендикуляр к линии Е'Е до пересечения в точке Fi нормали точки Е, получим радиус

Фиг. 38.

к траектории кривизны этой траектории в масштабе 1 мм-а м. Для определения нормального ускорения точки Е в абсо.лютном движении найдем величину нормального ускорения той же точки в дви-гкении относительно точки М, совпадающей в данный момент с полюсом мгновенного вращения Р, Скорость точки Е представлена на фиг. 39 отрезком ЕЕ. Если соединить точку Е' с точкой М и провести линию Е'Ь под прямым углом к линии Е'М, то получим отрезок LE, соответствующий нормальному ускорению в относительном движении. Ускооение точки М можно представить, по предыдущему, отрезком МО, т. к. точка М описывает при своем движении прямую линию,аналогично точке G (фиг. 34). При выбранном нами масштабе скорости отрезок ЬЕ = ЕЕ = ЁМ, а потому нормальное ускорение точки Е в абсолютном движении будет пропорционально отрезку

OEMO-LE МО-ЁМ. Перекинув отрезок ОЕ в положение ЕЬ (фиг. 39) и соединив точки и Е', мы получим радиус крршизны точки Е, проводя jE Fi под прямым углом к линии Е'Ь^.

Указанный только что метод нахождения нормального ускорения точки Е в абсолютном движении есть частный случай теоремы Эйлера, выражаемой следующим геометрическим равенством:

На фиг. 40 введены следующие обозначения: вектор Zp представляет полное ускорение точки В в абсолютном движении; вектор Zi представляет полное ускорение точки А в движении относительно точки В; вектор представляет полное ускорение точки А в абсолютном движении. По теореме Эйлера три вектора Z, Z,£ и Z всегда образуют замкнутый треугольник.

Применим эту теорему для нахождения ускорения ползуна в кривошипном механизме (фиг. 41). Разложим полное ускорение и jib на комионенты, соответствующие нормальным и тангенциальным ускорениям:

И введем масштаб ускорений у м/ск в 1 мм, выбрав для отрезок АО; но jj = а АО со, и следовательно у=а(о^, где to - заданная угловая скорость кривошипа, а а-масштаб че1)тежа. Разделив почленно ур-ие Эйлера на полученный масштаб ускорений, получим:

Фиг. 40.

ИЛИ

>z,

aib

zJiB-

Предположим, что угловое ускорение

кривошипа тоже дано, поэтому вектор г/т а

А ~ aoii

м. б. вычислен по ф-ле

0--,мм.

Величина Z,s найдется по ф-ле

aib

aib

а1 АВ

где Vaib - скорость точки А относительно точки В. Из тр-ка АОЬ, подобного полюсному тр-ку АРВ, мы найдем:

Va/b = ао} АЬ.

В этом ур-ии множитель а со представляет масштаб скорости. Следовательно

Этот отрезок можно построить, описав на шатуне АВ как на диаметре окружность

и засекая радиусом АВ на этой окружности хорду. Проекция АК хорды на диаметр даст искомый отрезок. На фиг. 42 дано построение мн-ка ускорений: от точки А отложен вектор Z, равный и параллельный радиусу кривошипа АО, а перпендикулярно к к нему отложен вектор zj, равный отрезку ОН, причем

ОИ-АОУ^мм.

Далее через точку А проведена .яиния параллельная нттуну и на ней отложен отрезок АК, равный Zaijj . Остается провести

две прямых линии: 1) через точку К под прямым углом к шатуну и 2) через точку Н параллельно линии движения ползуна до встречи этих линий в точке L. Полученный отрезок LH, помноженный на масштаб ускорений, дает величину ускорения ползуна В:

js = а 0)2 LH м/ск. Величина ускорения ползуна будет меняться, если изменять направление его движения, оставляя все остал1>ные величины неизменными. В этом случае мн-к ускорений (фиг. 42) сохраняет неизменной точку Я, а точка Е перемещается по перпендикуляру

1мм -а и

1мм - au) м/сн 1мм - аы м/сн-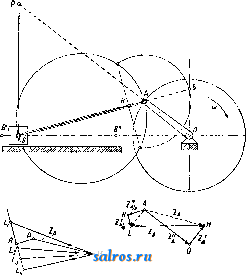

фиг. 41-43.

К шатуну, В зависимости от наклона линии hH, как показано на фиг. 43. Линия мертвых точек у таких кривошипных механизмов не проходит через геометрич. ось врашения коренного вала.

Рассмотрим теперь влияние масс в движущейся системе кривошипного механизма и определим ту работу, которая требуется для ускорения или замедления поступательно двигающихся частей и шатуна. Обозначим вес поршня, штока и ползуна-через Gi и вычислим массу всех реверсивно двигающихся частей

П1 =

9,Ы

кг

м1 CKi

Кинетич. энергия массы mi найдется по ф-ле:

Но vj = P-Ob, где - масштаб скоростей,

равный ,

следовательно

OA I

Найдем кинетичзск>-ю эчергию шатуна Е^, выделив элементарную масгу m (точка К на фиг. 44) и составив для нее выражение кн-

нетич. энергии - Для всего шатуна имеем:

= т(аРК)\

Выпажеш1е т{аРК) соответствует динамическому моменту инерции !;> относительно полюса Р. Но по известной ф-ле

где Ig-момент инерции шатуна относитель-

но его ц. т, (точка S на фиг. 44), а -масса шатуна, кинетич. энергия шатуна

Выражение copaPS соответствует скорости ц. т. шатуна г;, а потому

со {а. АО)

2 2

Далее из равенства сор(а-АР) определим сор:

СОр=а) ,

но 4=- = = (из подобиятр-ков AObsL АРБ) и потому

0)р=(0

Проведем в тр-ке АОЪ линию OS параллельно линии SP. Точка делит отрезок

ведена параллельно линии мертвых точек, а линия SjSi-параллельно отрезку Ob.

Л

Отрезок OS2 в масштабе /5= mckbimm

представляет скорость ц. т. шатуна, а потому выражение для кинетич. энергии Е^ будет иметь вид:

Заменив в этом выражении величину угловой скорости (О равновеликим выражением

о)= - и вводя в формулу длину L шатуна

В м, получим:

OA / j

Общая кинетич. энергия всего шатунного механизма, за исключением маховика и кривошипа с валом, выражается так:

й

E = Ej +E2

(1)

Величина, стоящая в скобках, имеет размерность массы и м. б. обозначена буквой Ш':

о

По предлолсению проф. Вмттенбауера, переменная величина Ш' носит название приведенная масса*, причем точкой приведения выбрана в напю.м счучае точка А-центр цапфы кривошипа. Введем обозначение:

ила

И заменим плпща.т;и квадратов ОЬ, АЬ я OSI площадями прямоугольников: у^-OA, У2 OA, Уз OA.

На фиг. 45 даны три квадрата, площади которых пропорциональны приведенным массам шатунного механизма для определенного положения кривошипа OA по отношению к линии мертвых точек, а на фиг. 4G, 47 и 48 указан простой графический прием определения величин: yi, у^ и у^. Построим диа-

Фиг. 44.

.4b в том же отношении, в каком ц. т. делит шатун АВ. Так как полюсом Р пользоваться в кривошипном механизме невозможно, то остается получить точку построением, указанньш на фиг. 44, где линия SS про-

граммы приведенных масс SJIJ, Ш2 и 3 по пути цапфы кривоппша, выбрав для основания диаграммы отрезок h в 120 мм или в 240 мм. Разделив окружность на 24 части и построив для первых 12 делений соответ-

ствующие положения шатунного механизма, мы найдем отрезки ОЪ, АЬ и OS2, а по этим отрезкам построим или вычислим ор-

Фпг. 4 7.

Фиг. 48.

динаты диаграмм у^, у г и у^. На фиг. 49 даны диаграммы (?!Jii, s), {Ш', s) и (9Кз,§); масштабы этих кривых по оси ординат соответственно равны

OA Ь2 OA ~ ОЛ

а, по оси абсцисс масштаб для всех кривых будет один и тот же: 1 мм-а' м, причем

, 2л-а. АО

1де h--основание диаграммы в мм. Зная величину приведенной массы Ш' для любого положения кривошипа, можно получить величину кинетической энергии Е, если будем располагать знанием скорости цапфы кривошипа Vji. В простейшем случае Va = Const, следовательно диаграммой кинетич. энергии может служить диаграмма {Ш', s), вычерченная в масштабе:

1 мм-q \кг ск]

Z== Х- 2,

где --масштаб кинетич. энергии.

Изменение кинетич. энергии на величину dE происходит благодаря работе внешней у, ]Ж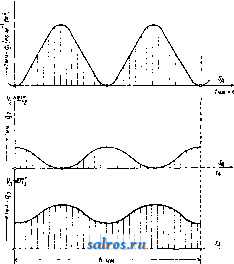

Фиг. 49.

СИЛЫ Т на пути ds, причем направление силы Т совпадает с касательной к кругу, описываемому цапфой кривошипа. Из ур-ия Т ds = dE ил1еем:

dz . , dx-a-

где 95-угол, образуемый касательной к кривой (Е, Sa). в более сложном случае скорость va будет переменной величиной, за-висяшей от пройденного пути s. Предпо-.яожим, что диаграмма (va, Sa) нам дана (фиг. 50), причем ординаты этой диаграммы представляют скорость va в масштабе /?1 м/ск-1 мм. Выражение для кинетич.энергии Е = - - - имеет в этом случае такой вид:

Заменим площадь квадрата у- площадг,ю равновеликого прямоугольника az, а пло-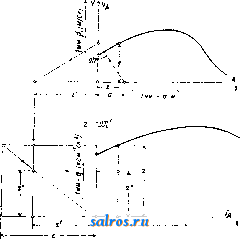

q Plac

замене Е = ~~

/им -ам

Фиг. 50.

щадь прямоугольника zz-площадью равновеликого прямоуго.чьника-rz . Нри этой

z . На фиг, 50 дано построение ординаты z . Проводя в точке N диаграммы (Е, Sa) (фиг. 51) касательную, мы можем по углу q> определить согласно пр(н дыдущему силу Т, , необходимую для ускорения движущихся масс в этом более слолсном случае. Приведенная масса имеет большое значение при решении общей задачи движения машины, включая и маховик. Если обозначить через Ijn

момент инерции маховика и принять радиус кривошипа равным i? f, то приведенная масса маховика найдется из соотношения:

стедовательно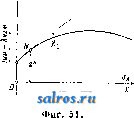

На фиг. 52 масштаб приведенных масс- принят 1 мм-q [кг м~ ск], а потому для приведенной массы маховика мы получим ординату

Y [мм].

Предположим, что диаграмма кинетич. энергии (Е, sj) нам известна по работе сил дви-жуп],их и сил сопротивления. На фиг. 52эта диаграмма представлена в масштабе 1 мм-А кгм по оси ординат и 1 мм-а' м по оси абсцисс. Вычертим новую диаграмму, т.н. диаграмму Виттенбауера, приняв для нее за абсциссы величины Y -\- у, а за ординаты величины Z. Полученные точки W этой диаграм-Ъ1ы лежат на замкнутой кривой, если рассматриваемое движение периодическое, в противном случае диаграмма получается разомкнутая. Из общего ур-ия

Е = --

l - SM - q Y + y

Соединим одну из точек кривой Виттенбауера с началом координат О и обозна-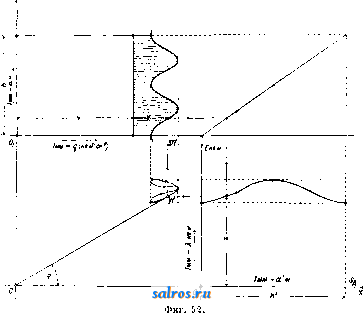

чим через tp угол наклона линии оси абсцисс. Так как

0W к

По этой формуле мы можем определить скорость в различных положениях цапфы кривошипа.

,Ыш.: М е р ц а л о в Н. И., Кинематша Л1еха-низмов, М., 1916; Р у н; е н ц е в С. К. и Иванов Б. А., Зубчатая и червячная передача. Редуктора, М., 1930; Левенсон Л. Б., Кинематика л1еханизмов, М., 1923; его же, Общая теория машин. Статика и динамика машин. П., 1923; С м и р-н о в Л. П., Кинематика механизмов и машин, М.-Л., 1927; его же, Кинетика механизмов и машин, М.-Л., 1926; R ей 1 е а х F., Lehrbucli d. Kinematik, В. 1 u. 2, Brschw.. 1875-19П0; G г a s-li о f F., Theoretisehe Maschinenlelire, B. 2, Hamburg- Lpz.. 1883; Burmester L., Lehrbuch d. Klrle-matik, Lpz., 1886-88; W 11 t e n b a u e г F., Gra-phische Dynamik, В., 1923; Hartmann W., Die Maschinengetriebe, Stg., 1913; T о 1 I e M., Die Rege-lung d. Kraftmaschlnen, 3 Aufl., В., 1921; P r о e-

ger F., Die Getriebekinematik als Riistzeug der Getriebedynamik, <;Forschungsarbeiten . Berlin, 1926, Heft 285; G r u b 1 о r M., Lehrbuch d. technischen Mechanik, B. 1, Bewegungslehre, 2 Aufl., В., 1921; Poschl Th., Lehrbuch d, technischen Mechanik, В., 1923; Beyer R Einfiihrung in die Kinematik, Lpz., 1928; Perry J., Angewandte Mechanik, Lpz., 1908; Kenned у A., The Mechanics <?f Machinery, L., 1907; Hart m a n n W., Ein iieues Verfahren zur Aufsucliung des Kriimmungskreises, Z. d. VDI , 1893, p. 95; К u t z b a с h, Maschinenbau , Berlin, 1927. Л. Смирнов.

МЕХАНИКА СТРОИТЕЛЬНАЯ, комплекс прикладных дисциплин, излагающих методы расчета сооруясений и их деталей. В понятие, обнимаемое этим комплексом, отдельными авторами и учебными программами втузов вкладывается весьма различное содержание. Невидимому правильнее всего М. с. рассматривать как объединение всех дисциплин, излагающих методы расчета сооружений в целом и их деталей, опирающихся на нек-рые общие для всех дисциплин основные гипотезы и положения. Основной задачей М. с. является расчет прочности как систем, представляющих собой отдельный стержень или брус, так и сооружений, являющихся сочетанием определенного числа отдельных стержней. Кроме изложения этой основной задачи курсы М. с . обычно заключают в себе и ряд вводньгх дополнительных глав, находящихся до нек-рой степени вне основного построения дисциплины. Отдельным разделам дисциплины в основной ее части дают названия графической статики (см.), сопротивления материалов (см.), статики сооружений. К вводным разделам дисциплины следует причислить такие главы, как статика сыпучих тел, и др. Следует также отметить, что все эти перечисленные главы не являются четко обособленными и самостоятельными частями предмета. Наоборот, все они связаны общностью гипотез и методики, сферы их действия в значительной степени переплетаются, и т. о. разделение задач М. с. по главам с вышеуказанными наименованиями представляется в значительной степени искусственным и произвольным, l самое последнее время, желая подчеркнуть общность методов М. с, с одной стороны, а с другой, учитывая неудобства в пользовании термином, позволяющим различное толкование, ряд авторов выдвигает новое название для этой дисциплины, именно- теория сооружений . Наименование это, хотя и безусловно удачное, не получило однако еще достаточно пшрокого распространения. Многие курсы М. с. содержат в себе также главы и отдельные ссылки, заимствованные из теории упругости , дисциплины, смежной с М. с. и обладающей некоторыми общими с ней исходными положениями, но все же принципиально от нее отличной как

�10042598891�55554�31�

в смысле особенностей методики, так и в смысле пределов применршости. Затем параллельно с рассмотрением вопросов анали-тпч. методами М. с. в отдельных курсах весьма часто приводятся результаты экспериментальных' исследований и испытаний различных материалов как в пределах упругой деформации, так даже и за этими пределами, хотя область остаточной деформации прииципнально исключается М. с. из рассмотрения. Обращение к результатам эксперимента объяснятся необходимостью обосновать прилолгимость апалитич. выводов М. с. к употребляемым в иил^еперной практике материалам и соорулсениям. С этой точки зрения соответствующее внесение в такую по существу апалитич. дисциплину, как сопротивление материалов, данных экспериментальных исследований представляется вполне обоснованным и даже необходимым.

Основными особенностями методики М. с. являются следующие три приема: 1).замена действительного сооружения условной расчетной схемой, 2) со.здание ряда рабочих гипотез и 3) ограничение своей задачи определенными рамками или пределами, именно такими, в к-рых принятые рабочие гипотезы не дают чрезмерного расхоледения с действительными явлениями в материалах или сооружениях. Первый из этих приемов, т. е. замена соорулжния его условной расчетной схемой,является основой построения всей дисциплины. Этот прие.м позволяет все разнообразие действительных сооружений нодве-сти под одну нз немногочисленных схем, раз-бираелтых в М. с, что придает этой последней необходимую обипюсть. Замена сооружения условной расчетной схемой основывается на сознательном игнорировании второстетген-ных моментов в работе материала и создании такой упрощенной схемы, которая отвечала бы только основным явлениям, имеющим место в данной конструкции. П[)имером использования этого приема яв.ляется замена расчета напр. такого пространственного и жесткого сооруления, как мост, состоящего из сквозных ферм с клепаными узлами, расчетом плоской пгарнирно-стержпевой системы. Замена действительной картины условной применяется не только по отношению к схеме сооружения, но и к действуюпшм на сооруление силам. Так, нагрузка, распределенная на весьма малую площадь по сравнению с основными размерами ссорулсения (напр. давление колеса паровоза), заменяется условной сосредоточенной силой, динамич. действие па лтостот проходягцего поезда заменяется действием системы условных статич. грузов величина к-пых выбирается с учетом динамич. воздействия фактич. нагрузки. Это приводе ште динамической и повторно действующей нагрузки к статич. уровню, т. е. к действию однократно прилагаемой статич. нагрузки, применяется почти во всех главах М. с, за исключением особых разделов, посвященных динамич. нагрузке. Одной из основных целей этих посиящшных динамике гпав является выработка т. н. динамич. коэф-тов, т. е. теоретич. обоснование перевода нагрузки к статич. уровню. Создание рабочих гипотез в М. с. ведется также путем

сознательного игнорирования второстепенных явлений и обстоятельств и пригшсыва-ния материалу в абсолютной степени тех свойств, к-рыми он обладает только в относительных, хотя и очень значительных, размерах. Подобное создание рабочих гипотез путем идеализирования свойств изучаемого объекта является типичным не только для М. с, но именно в пей, как в прикладной отрасли знания, этот прием получает особо широкое развитие.

Основной рабочей гипотезой М. с. является признание за рассматриваемыми материалами свойств идеального упругого тела. Этой гипотезой предполагается, что 1) вещество тела равномерно и неп[)орывно распределяется по всему его объему и 2) что'тело это однородно, т. е. обладает во всех своих точках и во всех направлениях одинаковыми свойствами, в частности упругими. При этом делается допущение,что выделяемые из этого тела бесконечно малые элементы будут иметь все те же физич. свойства, к-рымп обладает идеальное упругое тело в целом. Эти условные предположения, позволяющие применять в отношении явлений в материальных телах анализ бесконечно лгальгх, находятся в принципиальном противоречии с современными представлениями о строении твердых тел, имея в виду. Что больи1Инство материалов представляет собой агрегат из ко.мпопен-тов, резко отличающихся между собой упругими и прочими свойствами. Однако представляется в определенных пределах возможным признавать п за такими материалами свойства однородного тела, если такой материал обладает однородностью в стати-стич. смысле этого слова, т. е. если выделяемые из тела конечные объемы, достаточно большие, чтобы заключать в себе несколько зерен или кристалликов каждого компонента агрегата, но все же весьма малые по сравнению с обнп1ми размерами тела, будут обладать одинаковыми средними спойствалш.

В отношении идеальных упругих тел признается, что при отсутствии внешних сил тело при данной t° имеет определегшую форму и определенный объем. Для изменения формы и объема тела при неизменной t° необходимо приложение внешних сил, причем предполагается, что определенному изменению формы те.та соответствует и вполне определенная система сил, и обратно-определенной системе сил соответствует вполне определенное изменение формы тела. Случаи, выходящие из рамок этих предположений, рассматриваются в особых разделах дисциплины, посвященных неустойчивым формам равновесия. Далее предполагается, что по удалении внешних сил тело полностью возвращается к своей первоначальной форме, т. е. к естественному состоянию, за которым признаются свойства устойчивого равновесия. Гистерезис (см.) и влияние времени на протекание упругих явлений не учитьгеаются. В тех случаях, когда рассмотрению подлежат тела явно неоднородные, как напр. железобетон, тела эти искусственно приводятся к схеме однородного тела введением т. н, приведенных плонхадей.

Второй основной пгпотезой М. с. является условное предположение, что между дефор-