• Что такое фактурная штукатурка
• Выбираем сухие строительные смеси
• Преимущества напряженного железобетона
• Что влияет на выбор кровельного материала
• В чем преимущество пробковых полов

ция с раствором к CNS (15 %-ным): оранжевая или красная окраска, не исчезающая от прибавления HgClj [2]. Для качественной характеристики М. к. служит ее соль с хинином, имеющая Г„. 165°.

Новые заграничные патенты по получению М. к. вводят некоюрые усовершенствования в технику бродильного процесса. Имеются например предложения активировать жизнедеятельность бактерий (и препятствовать возникновению маслянокислого брожения) путем продувания в жидкость воздуха или кислорода, применяя периодрш. нейтрали--зацию образующейся М. к. малыми порциями мела или извести и т. д. Интересным является также предложение готовить М. к. из несбраживаемых пентоз - отбросов при получении спирта из осахаренной древесины (составляющих от 35 до 65% общей мас--сы получаемого сахара); эти пентозы сбраживаются вновь открытым видом бактерий при температуре 27° и дают смесь уксусной ж-ты и М. к. И. Для концентрирования растворов М. к. рекомендуются вакуум-аппараты с медной, бронзовой или свинцовой внутренней обкладкой. Для очистки и освет-те-ния технической М. к. кроме угля предложена обработка азотной к-той (при 85-95°), силикагелем, кизельгуром и т. п. Наконец вместо выпаривания или перегонки в вакууме предложено извлечение М. к. подходящими растворителями [J.

Лит.: 1) Е d е г R. и. К и 11 е г F., HeIvetica -chimica acta , Basel, 1926, В. 9, p. 557; о e г m u t h F., I. Eng. Chiem. , 1927, v.19, p. 852; з) м a r t e n E., Sherrard E., Peterson W. a. Fred E., ibid, p. 1162; 4) Ф. П. 582402/26; Г. П. 446865/27; 5) Ah. П. 290464/27.-W a g n e r A., Die lierstel-lung von Essigsaure, Garungessig, Buttersaure, Zitro-nensaure und Milchsaure, B. 2, Wien-Leipzig, 1926; X a Й к и h M. И., ЖХП , 1927, т. 4, p. 908; Che-niical and Metallurgical Engineering*, New Yorlt, 1926, V. 33, p. 423. B. Янковский.

МОЛОЧНЫЙ САХАР, или лактоза, CigHgaOn, принадлежит к дпсахаридам (био-зам) и является единственным углеводом, находящимся в молоке млекопитающих (в коровьем молоке 4-5%, в женском 5-5,5%); в растительном мире М. с. не найден. Наибо--лее вероятное строение М. с:

СНгОН СНгОИ

Р< 1, 5 > галактозидо-4 < 1, 5 > глюкоза *

М. С. образует бесцветн. кристаллы сладковатого вкуса. Имеются две формы М. с: -а и /3. Первая получается при кристаллизации из холодных растворов, а вторая- при кристаллизации из растворов, имеющих температуру выше 93°. Продажный препарат М. с. представляет собою гидрат с одной частицей воды-CiaHjaOu-HjO; он име--ет уд. вес 1,525; при нагревании до 87° начинает плавиться; при 100-110° он постепенно теряет всю кристаллизационную воду; нагревание до 150-165 вызывает побурение;

* Числа в скобках < > показывают номера атомов углерода, связанных кислородным мостиком.

при 170-180 наступает т.н. карамелиза-ц и я; (с разложением) около 200°. В растворах М. с. присутствуют обе его формы: а и р. Растворимость М. с. в воде: при 0°- 10,6% (4,0% а-формы и 6,6% Д-формы); при 20°-16,1% (6,2% а и 9,9% /3); при 50 - 30,4% (12,1% а и 18,3% jS); при 100°- 61,2% (26,3% а и 34,9% /8). В спирте и эфире М. с. нерастворимы. Уд. вес водных растворов при 20° (по Шмегеру):

Концентрация Уд. в. Концентрация Уд. в. в % в %

2,3544 1,0071 14,8.548 1,0566

5,0949 1,07.il 20,0506 1,0783

10,1650 1,0376 24,7852 1,0992

Удельное вращение растворов М. с. почТи не зависит от концентрации, но в сильной степени зависит от °. Общая ф-ла для удельного вращения М. с. дана Гетпером: [a]jj =-Ь 55,3-0,06 (f-20).

В среднем [а]* = --55,24°; для а-формы

[аТо = + 90°, для /5-формы [а] = -Ь 35°. М. с. обладает свойством мутаротации (см.); у свежеприготовленных растворов [а] = 85-i-90°;нopмaльнoe удельн. вращение достигается после 24-ч. стояния либо при нагревании до кипения или прибавлении аммиака. 1 г М. с. восстанавливает 148 см фелингова реактива (приготовленного по Сокслету); щелочами М. с. окрашивается в желтый цвет, с фенилгидразином дает озазон, который плавится, разлагаясь, при t° 213-215; при окислении HNO3 М. с. дает слизевую кислоту. Продолжительная инверсия сильными кислотами вызывает гидролитическое распадение молочного сахара на d-глюкозу и d-галактозу:

С12Н22О11 + Н2О = СбН120в + CeHisOe.

d-глюкоза ё-галактоаа

Распадение М. с. может происходить и под влиянием микроорганизмов при помощи особых энзимов-л а к т а з; они расщепляют М. с. и оба продукта расщепления переводят в молочную кислоту (см.). В технике молочного хозяйства имеют важное значение следующие виды бронсения: молочнокислое (скисание молока), спиртовое (приготовление кефира, кумыса, айрана), пропионовое (в сыре) и маслянокислое (вызывающее пороки масла).

Аналитическое определение М. с. Качественно М. с. открывается следующими реакциями. 1) Испытуемую жидкость насыщают при нагревании уксуснокислым свинцом; затем осторожно ц^эибавляют аммиака до растворения первоначально образующегося осадка и кипятят 2-3 минуты: смесь окрашивается в красный или оранжевый цвет. 2) К исследуемому раствору прибавляют HNO3 (удельного веса 1,14), выпаривают на водяной бане до V, объема и оставляют стоять 12-20 ч., после чего смешивают с небольшим количеством воды: выпадают кристаллы слизевой к-ты, к-рые отсасывают, промывают небольшим количеством воды, высушивают и определяют по 1°пл. (213°). Количественно М. с. определяется поля-риметрич. путем или весовым при помощи фелингова реактива.

Технически М. с. получается из молочной сыворотки. После осаждения из молока казеина при помощи сычужного фермента- ляба, сыворотку отфильтровывают и в присутствии углекислого кальция упаривают под уменьшенным давлением; вьвделив-пшйся М. с. вновь растворяют, обесцвечп-

вают кипячением с углем, сгущают и пере-кристаллизовывают. М. с. применяется главным обр. как пищевой продукт - для искусственного вскармливания младенцев и в различных питательных препаратах; незначительные количества его идут на приготовление некоторых гигиенических препаратов (например таблеток для дезинфекции рта) и как примесь к казеиновым краскам (при крашении бумаги). В военной и декоратив-. ной пиротехнике, в театральной технике и т. п. М. с. находит применение как составная часть горючих дымовых смесей и фейерверков, играя в них роль дымообразующего или замедляющего горение вещества.

Лит.: и н и x о в Г. С, Химия молока и молочных продуктов, Химико-физич. свойства, ч. 1-Молоко, его составные части, 2 изд., М.-Л., 1928; L i р р-m an п е., Chemie der Zuckerarten, 3 Aufl., В. 2, p. 1520-1584,Braunschweig, 1904; Oppenheimer C, Die Fermenteund ihre Wirkung, B. 1-5, Leipzig, 1925-29. И. Щербаков.

МОМЕНТ, в широком обобщенном смысле произведение двух величин различных физических размерностей, причем одна из этих величин является длиной или степенью длины. Если вторая величина м. б. разбита на элементы, то М. составляется из суммы отдельных элементарных М. Первая величина-длина--геометрически изображается отрезком, вторая-либо точкой либо направленным отрезком. Обычно наименование М. относят к этой второй величине, т. е. говорят о моменте этой второй величины. При вычислении М., а также при геометрич. изображении его, всегда ориентируются или относительно какой-нибудь определенной точки (полюс, центр М.) или относительно прямой (ось), иногда относительно плоскости. М. придают либо только

-----О численное значение (существенно

ч| положительный М.) либо припи-

сывают кроме того и знак плюс или минус. Пусть один множитель Фд, произведения, составляющего М., выражается направленным отрезком, т. е. вектором А (фиг. 1); задаемся точкой О в качестве полюса. Численное значение для М. вектора А будет произведение A-d, где d-длина перпендикуляра из точки О на направление вектора А (d--длина, о которой говорится в определении момента). Меняя направление вектора А на противоположное, мы согласно определению получим то же самое численное значение для М. Между тем в практич. вопросах желательно различать эти два случая. Для этой цели приписывают М. в одном случае знак плюс, а в другом минус (в каком случае плюс и в каком минус-зависит от условия), например исходя из следующего соображения. Воображая плоскость через данный вектор А и точку О, укрепленную в полюсе О, вращают эту плоскость по направлению вектора вокруг точки О; если вращение происходит по движению часовой стрелки, то М. приписывают знак плюс, в противном случае-знак минус. В этом условии имеется неопределенность: одно и то же вращение будет казаться происходящим и по движению часовой стрелки и против, в зависимости от расположения наблюдателя над' или под плоскостью вращения. Однако при постоянстве места наб-

т. Э. т. XIII.

людателя два различных вращения всегда будут отмечены разными знаками у М., чего в сущности и достаточно. Впрочем эту неопределенность легко устранить введением понятия о лицевой стороне и изнанке плоскости или изображая момент вектором, перпендикулярным плоскости, проходящей через данный вектор а и точку О, и условившись направлять вектор М. согласно правилу штопора.

В интерпретации векторного исчисления, (см.) момент М вектора А относительно полюса О можно представить в виде векторного произведения

М=[гА],

где г--радиус-вектор начальной точки данного вектора а относительно точки О.

Отнесем данный вектор А к произвольной прямой I, принимаемой за ось М. Для построения и вычисления М. вектора а относительно оси I поступают след. обр. Проводят плоскость S перпендикулярно к оси I: пусть точка пересечения плоскости с осью будет О; проектируют данный вектор а на эту плоскость S и определяют М. проекции вектора А на плоскость S относительно полюса О; этот М. и называют М. вектора а

относительно оси. д. Колянновский.

М. инерции плоских фигур. При изучении изгиба, кручения , в задачах гидростатики приходится встре-чатьсн с М. инерции плоских фигур. Осевым, или экваториальным, М. инерции плоской фигуры относите.ть-но оси ОХ, лежащей в ее плоскости (фиг. 2), называется предел суммы произведений из элементарных площадок do) этой фигуры на квадрат расстояний их у от оси ОХ:

1х- J ydco, (1)

где интегрирование распростоанено по всей площади О). Подобным же образом относительно оси 0Y:

Фиг. 2.

doD.

Полярным М. инерции этой жэ фигуры относительно точки О называется

Jo = / rdco, (3)

где -расстояние элемента dco от точки О.

Ясно, Ч'ОО

1о = 1х + 1г- (4)

Центробежным М. инерции относительно дзух осей ОХ и 0Y называется

IxY=Jxydo). (5)

Размерность всех этих величин-[длина]*. М. инерции всегда положительны и отличны от 0; центробежный момент м. б. положительным, отрицательным или жэ нулем. Если точка О совпадает с ц. т. С плоской фигуры (фиг, 3), то соответственные М. инерции

Табл. I.-.

1/12

0,289а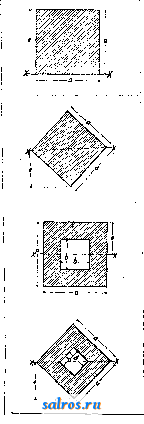

и = а^, е = а; /

Х~ 3

j/2 -X 12

Wy = - -г:0,И8о8; е„= 0.289а

а , а*-Ь* 2

Х=6а ; X=j/ -J0,289l/a. + 6*

. I.-П л О щ ад и .0), моменты и я е р ц и и /х. моменты сопротивления Wx и радиусы инерции

(е-расстояние от нейтральной оси сетения до наиболзе удаленной точки его.)

т

плоских фигур.

а а*~Ъ*

= а2-Ьз, е = ~0,707а; = ; ]/2 .12

и^ = --*>0,118; л 12а а

ех=]/ -S0,289/aa + t,8

2 X 12 x 6 x у^2

ca = bh-kc, e = ; I,

2 12

bhs-cfts

1/ ьч .

i)h.S (7j cos a f b sin a); j=(l C0S2 a + Ь sin* a);

bh /hacosgg + bsingnX -X 6 \ hcosa + bsina /

-t/~ftCQS + bsinag у 12

0,289)/Л2сО8 а + b-Slna

J R 00

e co I

Э l o 11

И

Sill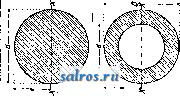

I ! I

g I

a) +

co я

Табл. 1.-Площади ш, моменты, инерции 1х, моменты сопротивления Wx и радиусы инерции плоских фигур.

(е-расстояние от нейтральной оси сечения до наиболее удаленной точки его.) (Продолжение.)

г>0.519Я

o)l,5708(H2-r2),

ш = лаЬ^З,1ШаЬ, e = a; J= 0,7854аЗЬ;

o} = n(ab~cd)S,U16{ab-cd), e = a; = (aS Ь - dSc) 0,7854(a b - d4);

... .(a36-d3c) asb-dsc l/aSb-dc

W =---j-- 0,7854 --; ет=о1/ ~-:j

л 4a a л 2 r ab-cd

o. = dt + 2a(s + n), e = ;/=bd -(W-l4) 5

Г 1 1 *i

bd3-(m-u)Jv

6d

l/l[-4<->] r dt +2a(s +n)

o)= d( + 2a(s + n), 6

= [(+ +f(b* - **] *

) = dt + a(s+n), e = -; Z y =

= 2[bd3-±(mh)

bd3-(m-I4)

1 Ada -

12[dt + a(s +n)]

f< = df+ a(s+n), e=b-

! + -t-(b-t)2(b+2t)*

2sb3 + u3+ (Ь4 {4)

dt +a(s+n)

<o(b-e)2;*8

ЦТ + i)

+ Tn + a(s + n),-

e = d + +2am(m + 3s)

® 0,5i(r + t)+ Tn+a(s + n)

, 3i d2-Z(T-t)(3d-0

0,5UT + f)+Tn+a(s+n) I = --[/8(T + 30 +46n3-2atn3]-a)(d-e-n)2;

o> = 0,5I(r + f) + Tn + a(s+n), e =

sb3 + mr3+ zt3 , ат[2аг + (2а+ЗГ)г] Й + 36 +

UT-t)[(T-t)a + 2(r + 2t)g]. 144

♦I ff-уклон полок, равный tga-

h-l b-t

где a-уклон внутрен. полки к горизонту.

* 2 ff-уклон полок, равный tga

h-l 2(b-t),

где а-уклон внутрен. полки к горизонту.

О 1 со i IN I

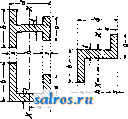I в I 8 -

>

и

I l

II

---ь!г-

Пластина пренебрегаемо-малой толщины

Стержень пренебрегаемо-малого поперечного сечения

Род тела

а с Н а а

Круговой цилиндр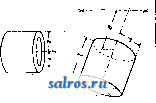

col +

Род тела

Ш

Круговой цилиндр

Пластина пренебрегаемо-малой толщины

Прямой круговой конус

Пирамида с прямоугольным основанием

Прямоугольный параллелепипед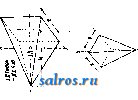

11 ы 73-

1Г

Шар

Прямой круговой усеченный конус

1т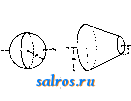

I I I

о

н

ш

Кольцевая тора

Параболоид вращения

Трехосный эллипсоид

Шаровой сегмент

Шаровой сектор

Род тела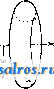

называются центральными моментами Ixci Itc и Iqc- М. инерции 1 относительно осей EU и EV, параллельных осям СХ и CY и находящихся от них на расстояниях аи. Ь:

Iu=Ixc + fb\ ly-lYC + a- (6) Полярный М. инерции относительно точки Е: I=Ioc + col\ (7)

где Iqc-полярный М. инерции относительно ц. т. С. Из (6) и (7) видно, что М. инерции относительно ц. т. являются наименьшими. Центробежный момент Iy относительно новых осей EV и EU, параллельных прежним CY и СХ на расстояниях а и Ь:

Iuv= 1хт + ((Ь. (8)

М. инерции относительно оси OA, составляющей угол а с осью ОХ:

1 = 1х cos a + jysina - I XT sin 2a. (9) Если выбэрем угол a так, чтобы

tg2a=-, аО)

то получим два взаимно перпендикулярных направления OA и ОВ, для к-рых центробежный М. инерции 15=0, а М. инерции до-

у и

Фиг. 3.

Фиг. 4.

стигают наибольшего и наименьшего значений Ii и Jg. Эти оси называются главными осями, а Ii и - главными М. инерции.

1г= 2 Их+17) + 2 vax-ijf+A

Для любых осей

1а = ii cos2 а -I- Jg Sin2 a. (12)

Г.т1авные оси, проходящие через ц. т. С, называются главными центральными осями инерции, а моменты относительно них^-г л а в и ы м и центральными М. инерции. При наличии в контуре фигуры оси симметрии последняя является одной

из главных осей. Длина g =]/ называется радиусом инерции площади а> относительно оси Оа. Если по направлению луча Оа откладывать отрезки, обратно пропорциональные длине соответственного е, то концы этих отрезков нри вращении Оа около точки О расположатся по так наз. эллипсу инерции, ур-ие к-рого

+ 1гП = Const; его оси совпадают с главными осями инерции плоской фигуры. Эллипс инерции дает наглядную картину изменений М. инерции при повороте осей около точки О. Если отложить на главных осях отрезки и

по направлению, перпендикулярному к оси (фиг. 4), и на Зтих отрезках построить эллипс, то он будет подобен первому эллипсу и назьшается вторым эллипсом инерции (Кульмана). По этому эллипсу инерции М. инерции относительно любой оси определяется выражением вида

где od-расстояние от ц. т. эллипса до касательной, проведенной параллельно оси ОХ. Центробежный М. инерц^пг определяется произведением Ixj = со od ос. М. инерции для правильных фигур и для фигур, составленных из правильных, вычисляется по ф-лам (1) -(5). Для неправильных ф iryp применяется следующий вычислительный прием: площадь данной фигуры разделяют рядом прямых, параллельных оси ОХ, на полоски настолько узкие, чтобы их можно было рассматривать как прямоугольники. Определяют по чертежу площадь каждой полоски 1, (Ug, ... и расстояние у ее ц. т. от оси ОХ. Тогда приближенно

(13)

х=2К + 1П-

Вторым членом при малой ширине полоски Ь, можно пренебрегать. При графич. определении М. инерции фигуры (фиг. 5, а) величины coi, ft)2, ... изображают в виде векторов, приложенных в ц. т. каждой полоски, строят для них силовой мн-к (фиг. 5, б) с полюсным расстоянием Н и по нему веревочный мн-к (фиг. 5, в), продолжая стороны его до пересечения с осью Х-ов; приняв затем полученные на оси Х-ов отрезки за силы, приложенные в ц. т. указанных полосок, строят для них второй силовой мн-к (фиг. 5, г) с полюсным расстоянием Hj и по нему строят второй веревочный мн-к (фиг. 5, д), продолжая стороны его до пересечения с осью Х-ов.

©

/ТУ .ЪЛ. f\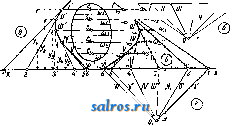

Фиг. 5.

По этим построенршм момент инерции 1х определяется приближенно следующими выражениями:

1х=Г6 -Н-Н' = 2<о,-Н, (14)

в к-рых: 16-отрезок, отсекаемый крайними сторонами второго веревочного мн-ка на оси Х-ов; со-площадь, ограничиваемая крайними сторонами первого веревочного мн-ка и осью Х-ов. Можно также для вычисления М. инерции пользоваться интеграторами. На фиг. 6 показана схема интегратора Амслера. При определенрш М. инерции фигуры относительно оси XX устанавливают прибор так, чтобы линейка SS была параллельна оси XX; для этого служат две линейки Р и Т равной длины, снабженные