• Что такое фактурная штукатурка
• Выбираем сухие строительные смеси
• Преимущества напряженного железобетона
• Что влияет на выбор кровельного материала
• В чем преимущество пробковых полов

ваема как состоящая иа силы F и пары сил (F, ft), т. о. силу J можно перенести, сохраняя ее величину и направление, в другую точку тела, прибавив при этом соответствующую пару сил. Момент пары сил, которую следует прибавить, равен (см. Натра сил): MiFrl, (174)

или, если обозначить вектор OA через г = = - то

MlrF\. (174)

Последний вектор определяет также момент силы F относительно точки О. Если длина перпендикуляра, опущенного из О на линию действия силы F, равняется d, то получаем:

M = Fr sin {F, г) = Fd. (174 ) Нетрудно видеть, что если О лежит на линии действия F, то т. к. в этом случае d=0, то и ikf = 0; Ж = 0. Пользуясь ф-лями векторного исчисления, имеем из (174):

М^ = yZ-zY

.My=zX-xZ

(175)

M,= xY-yX где x, у, -координаты точки А по отношению к системе осей с началом в О, а X, У, Z-модули компонент F по 3THiM же осям. Векторы Mx=MJ; My=-Myj\M-=MJc называются моментами силы F по отношению к осям координат. В частности, если F лежит в плоскости ху, то т. к. 2 = 0 и Z = 0, имеем из (175):

Ма; = 0; Му = 0; M = xY-yX. Последнее равенство представляет собой также момент рассматриваемой силы F относительно начала О. Отсюда видно, что проекция момента какой-либо силы, взятого е)тносительно нек-рой точки, на какую-либо ось равняется моменту проекции силы на плоскость, перпендикулярную к оси, взятому по отношению к точке пересечения оси с плоскостью. Если к телу приложены п сил F-i, F,Fn, то, взяв на теле произвольную точку О, можно к ней перенести все данные силы, сохраняя их величину и направление и прибавляя соответствующие этим переносам пары сил, моменты к-рых по (174) будут равны:

M, = [r,F,] (г==1, 2, п), (176)

а модули моментов определяются равенствами (175). Все силы Fi, F2, F, приведенные к точке О, м. б. затем заменены одной равнодействующей силой:

F-F,= Fi, (177)

а все пары-т-одною равнодействующей парою, момент к-рой (см. Нара сил)

Ж=2--11[**/г]- (178) 1 1

Последний вектор назьшается главным моментным вектором системы сил по отношению к данной точке приведения сил. т. о. всякую систему сил можно привести бесчисленньм множеством способов к одной силе и одной паре сил. Очевидно для того, чтобы силы данной системы взаим-

но уравновешивались, необходимо и достаточно, чтобы как сила JP, так и главный мо-ментный вектор М равнялись нулю, т. е. чтобы

=2 .- = 0 1

71 П

MMilr.F.lO

(179)

что равносильно наличию шестр! ур-ий:

2-Х,-=0; 2г = 0; 2Z, = 0; (179) 1 1 1

п п

2 (.Vi Zi - Zi У,) = 0; 2 - Хг Zi) = 0;

(xiyi~y,Xd=0. (179 )

В частности, если система сил сходящаяся, то для равновесия системы необходимо и достаточно наличия только трех ур-ий (179), если система плоская-необходимо и достаточно наличия двух каких-либо уравнений (179) и соответствующего одного ур-ия из (179 ); если же наконец система плоская и сходящаяся, то для равновесия системы необходимо и достаточно наличия только двух из ур-ий (179).

Допустим, что данная система сил, приведенная к точке О', дала равнодействующую силу F и равнодействующую пару момента 31. Если мы возьмем затем другую точку приведения О, то равнодействуюпщя F остается та же; изменится лишь главный мо-ментный вектор, превратившись в

Мо = М + М\ (180)

где Ж'-момент той пары, 1оторую следует прибавить при перемещении F из О' в О (фиг. 51). Разлолшм момент М (фиг. 52),

. ,

Фиг. 51.

Фиг. 52.

получршшийся при приведении системы сил к точке О', на две составляющие: Ма-по направлению равнодействующей силы F и Мр-по перпендикулярному к F направлению. Проведя к плоскости (JP., 31) в точке О' перпендикулярную прямую, можно очевидно найти на этой прямой такую точку Oi, что при перенесении силы jP из О' в Oj нужно будет прибавить пару момента jM= = -Жр. т. о. при приведении данной системы к точке Oi и получаются сила F и.три момента пар 31а, 31 р и Ж', причем последние два момента взаимно унргчтожаются, так что остаются только сила F и направленный по ней момент пары 31 . Отсюда видно, что всякую систему сил можно привести к одной силе и одной паре, момент которой совпадает с направлением силы (см. Винт в т е о-ретич. механике). Из вьппесказанного следует, что всякой точке тела при данной

системе сил соответствует определенная пара векторов JPh Ж; при переходе от одной точки тела к другой меняется лишь вектор м, вектор же f один и тот же для всех точек тела. Нетрудно однако убедиться, что если провести какую-нибудь прямую I, параллельную jF, то моментный вектор для всех точек этой прямой будет один и тот же. В самой деле, пусть система сил, приведенная к точке О, не лежашей на I, дала векторы F и Ж. Т. к. расстояние d от О до I остается одно и то же, какую бы мы точку на прямой I ни взяЛи, то, как видно из (174 ), момент Ж' силы JP по отношению к любой точке О' прямой I будет один и тот же, почему при приведении системы сил к любой точке прямой I придется к Ж прибавлять один и тот же вектор Ж', что и доказывает вышеприведенное предложение. Отсюда следует, что если провести плоскость S, перпендикулярную к F,to, исследовав характер изменений вектора М для всех точек этой

плоскости, мы тем самым исследуем характер этих изменений для всех точек тела. Если точке Ох плоскости S (фиг. 53) соответствуют векторы F и Мх\ \ F,то,перейдя к другой точке О той же плоскости, т. е. перенеся силу F из Ох в О, получим от этого переноса новый момент Ж', перпендикулярный плоскости {Мх, 0x0), причем М' = ==F-OxO, и главный момент относительно О будет:

М = Мх+М', (181)

М^ = М\+ М'2 = М\ -Ь ОхС^ (1810

Фиг. 53.

или

М'

(ISlO

где S- угол между М я М \ Если провести в плоскости Я из Ох радиусом Охб окружность, то так как М' для всех точек окружности один и тот же, то и М для всех этих точек при данной системе сил есть величина постоянная, причем, как видно из (1810 и (181), с удалением О от Ох величина М увеличивается, а вектор Ж все больше наклоняется к плоскости S. Если перейти к точкам в пространстве, то нетрудно усмотреть, что все точки, лежашие на круглой цилиндрической поверхности, ось которой проходит через точку Ох, перпендикулярно (S, будут иметь одну и ту же величину М. Ось цилиндра, представляюшая геометрич. место точек, по отношению к к-рым данная система сил приводится к совпадающим по направлению силе F и главному моменту 31, называется центральной осью данной системы сил. Очевидно, что для точек центральной оси величина М достигает своего минимума. В частности, если в точке Ох главный моментный вектор равен нулю, то система сил для всех точек тела приводится к одной силе F. Очевидно в этом случае п п

м fsfi-fio, (182) 1 1

или по (1740

S[I/]-i;i = 0. (1820

Если же F=0, то пололсение центральной оси становится неопределенным, так как вся система сил приводится к паре, момент которой Ж свободен, т. е. момент к-рой м. б. перемещаем параллельно самому себе в любую точку тела (см. Пара сил).

При выводе условий равновесия (179) мы полагали, что тело, к которому прилонсены данные cилыFl, Fg,F , свободно. Допустим однако, что тело находится под воздействием не только сил F, но и нек-рых связей. Очевидно, что, присовокупив силы реакции связей к данным силам Fi, мы можем тело вновь рассматривать как свободное, к к-рому следовательно применимы условия равновесия (179), с тем однако отличием, что в числе сил Fj- этих равенств находятся также и силы реакции связей. Допустим, в теле имеется неподвижно закрепленная прямая, вокруг которой оно способно вращаться. Выбрав эту прямую в качестве оси Z (фиг. 54), зафиксируем на ней начало О, к к-рому приведем систему сил, приложенных к телу. Действие равнодействующей силы F очевидно уничтожится реакцией неподвижной оси: главный же моментный вектор Ж м. б. разложен на компоненты М^, Ж„, Ж^. Силы пары, момент к-рой равен Ж^ параллельны оси у и приложены к точкам неподвижной оси, вследствие чего действие их уничтожается реакцией оси;точно так лее уничтожается действие па-у ры, момент которой равен My. Остается только пара с моментом Ж^, вращающая тело около оси z; момент называется

вращающим моментом. Для того чтобы рассматриваемое тело находилось в равновесии, необходимой достаточно,чтобы Mg=0, т. е., как видно из (1790, чтобы

2№-?/Д,)-0. (183)

Т. о. вместо 6 ур-ий (1790 и (179 ), необхо-димьгх и достаточных для равновесия системы сил, приложенных к свободному телу, мы здесь имеем лишь одно необходимое и достаточное условие для равновесия. Остальные же пять ур-ий определяют силы реакции оси, приложенные к телу, к-рые очевидно состоят из силы -F и пар, моменты которых равны -Жя, и -My. Если ось Ое может перемещаться вдоль своего направления, то уравнения (183) недостаточно для равновесия тела, необходимо еще, чтобы

(184)

т. к. в этом случае не может возникнуть си л а реакции вдоль направления оси, кото pan

уничтожила бы действие силы Z. Если тело имеет только одну закрепленную точку О, то, приведя систему сил к этой точке, нетрудно видеть, что сила F уничтожается реакцией неподвижной точки, так что остается пара момента М. Следовательно для того, чтобы тело в рассматриваелюм случае находилось в равновесии, необходимо и достаточно, чтобы ЗГ = О, т. е., как видно из (179 ), чтобы имели место следующие 3 ур-ия:

2(iX,-,Z,) = 0 1

(x,Yi-yiXd = 0

(185)

Т. о. при наличии тела, имеющего непод-виячную ось вращения, необходимо и достаточно для равновесия одно условие (183); если эта ось мож;ет перемещаться вдоль собственного направления, требуются два условия-(183) и (184); если же тело имеет лишь одну неподвижную точку, требуется уже для равновесия тела три условия (185).

Отсюда следует, что чем тело свободнее, тем больше условий, налагаемых на силы при равновесии тела. Тело, имеющее неподвижную ось, обладает одной степенью свободы, так как положение тела определяется одним параметром-углом поворота тела около оси; в соответствии с этим имеется только одно условие равновесия. Если эта ось может перемещаться вдоль своего направления, то тело обладает уже двумя степенями свободы, и в связи с этим имеются два условия равновесия тела. Если тело наконец имеет одну неподвинсную точку, то, так как положение тела определяется тремя параметрами (см. Координаты), имеются 3 условия равновесия и т. д.

Допустим, что имеется те материальных точек А-1, А2, .... координаты которых соответственно Xi, yi,2i; Жа, Уг, z-i] ...; ж , у^, ? и к к-рым прилонсены силы F, F, F. Допустим далее, что эти точки находятся под воздействием нек-рых связей, что аналитически выражается в том, что Зп координат точек связаны между собою некоторым числом уравнений:

/i (Жь Уи Zi, Жз, 2/8, Zi, ...; ж„, у„, z ) = 0 \

::::::::::::::::::::;:::;[ (б)

и (xi, Уи Zi, Жа, уг, Z2, ...; ж„, Уп, г! ) = 6 i число к-рых пусть будет р. Из общего числа Зп координат Зп-р м. б. взяты совершенно произвольно, а остальные р координат м. б. выражены через произвольно взятые при помощи ур-ий (18G). Поэтому число Зп-р и определяет степень свободы рассматриваемой системы точек. Очевидно, что р не м, б. больше Зп. Если р = 3и, то координаты всех точек системы вполне определяются из (186 , т. е. система неподвижна; если же р=0, то все точки системы свободны.

Пусть равнодействующая всех реакций связей, действующих на- какую-либо точку Аг системы, равна Щ (t 1, 2, п), так что эта точка находится под действием силы.

равной Ff+Bi- Следовательно для того чтобы вся система нахоцилась в равновесии, необходимо, чтобы

Fi-b-Bf-O (г=1, 2, ...,п), (187) что равносильно наличию Зп ур-ий Xi -\- Xi =0; Yi + Yi = 0; -f Z = О

(г = 1,2.....n), (187)

где Х{, Yi, Z,-модули компонент 22 по осям координат. Выше было показано, что в случае одной несвободной точки сила В будет нормальна к кривой или к поверхности, осуществляющей связь, и что следовательно полная работа Т' силы В равна по (158) нулю: *

dT BdrQ; Т' = jB-drO.

Несмотря однако на то, что при наличии системы несвободных точек реакции связей м. б. совершенно другие, чем реакции кривых линий или поверхностей, условие (158) имеет место и в данном случав, так что JRj--rfr,. = 0, и следовательно

Bi-dr;0.

(188)

Последнее ур-ие, являющееся основным уравнением движения системы несвободных точек, м. б. интерпретировано след. обр.: реакции связей, действующих на систему материальных точек, не могут в своей совокупности ни пог.тощать ни давать работу, хотя для отдельных сил реакций это является возмояс-ным. Это предложение стоит в связи с принципом сохранения энергии, ибо, поскольку осуществление связей не влечет за собой ни затраты энергии ни получения таковой, постольку реакции связей не могут ни поглощать ни давать никакой работы. Исходя из (158), (158) и (188), можно в отношении системы точек притти к точно таким ясе выводам, что и в отношении одной материальной точки, а именно: точки рассматриваемой несвободной системы, находящиеся сначала в покое, начинают кагкдая свое движение по направлению соответствующей равнодействующей сил Fi и Bi, так что в начальный элемент времени имеем:

J;(P,-f-B,).dr>0, (189)

или, принимая во внимание (188):

F,dri>0.

(190

т. о. в начале движения сумма элементарньпс работ всех движущихся сил Fi положительна. Если же в числе всех возможных перелте-щений, допускаемых данными связями, пет ни одного, для которого неравенство (190) имело бы место, то очевидно, что система в движение притти не может; другими словами, необходимым условием для равновесия системы несвободных точек является неравенство:

2(F,rfr,)<0, (191)

где символом (Уг, обозначены возможные, или виртуальные, т. е. допус-

каемые связями, элементарные перемещения точек, в отличие от действительных элементарных перемещений точек, обозначаемых dr,-. Неравенство (191) выражает т. п. п р и н-цип (начало) возможных перемещений, или принцип возможных, или виртуальных, работ (Бернулли, 1717). Пользуясь ф-лой векторного исчисления, неравенство (191) можно представить еще и в следующем виде:

2(Xi 6Xi -Ь Г, Sy, + Z, dzd О, (19Г) 1

где 6Х{. 6у^, 6Zi,-модули компонент по осям координат вектора Sr,-. Если уралнепгя г-вя-зей не содержат неравенств, а даны нанри-мер равенствами вида (18G), то всякой системе возможных перемещений дг{ соответствует система возмолсных же, но противополож;-ных перемещений -rfr-, так что, если система точек находится в положении, при котором п

< о, то будет иметося система пере-

п

мещений, для которых^ 6i\ > 0. В этом 1

случае равновесие будет иметь место, если при всех возможных перемещениях существует равенство:

Fr6r,=

= 2 (Xi бх, + Г, ду, + dzi) = 0. (192) 1

Значение принципавозмо:кных перемещений заключается в том, что при его применении нет надобности знать для определения условий равновесия несвободной системы точек ни характера механизмов, осуществляющих данные связи, ни величины реакций их; для этого достаточно знать лишь все возможные элементарные перемещения точек системы при данных связях.

Допустим в частности, что все возможные перемещения, или вариации перемещений, rf-Tj- совершенно произвольны, т. е. что точки системы свободны. Тогда, положив все вариации координат бх, биг, бг, бх, ... равными нулю за исключением по-.тучим из (192):

Zn6zn = О или Z = 0. Точно так же получим:

Xi = 0; Fi = 0; Zi = 0; 2 = 0 и т. д., так что вместо равенства (192), выражающего условия равновесия, получим равенства:

:Fi = 0; JF2 = 0; ...; F = 0,

что конечно совпадает и со сделанными ранее выводами. В противоположном крайнем случае, т. е. когда все точки систем не могут менять своего положения, так что: 6rf=0, (t=l,2,3,...,w), равенство (192)тождественно удовлетворяется при всевозможных силах Fi,T.e. система будет в равновесии, каковы бы ни были силы Fi, что конечно очевидно.

В общем же случае при наличии р ур-ий связей (186) для системы точек, имеющей 3w -р степеней свободы, можно притти от ур-ия равновесия (192) к ур-иям равновесия.

связываюшим компоненты сил с координатами точек, след. обр. Из общего числа 2>п вариаций 6Xi, 6у{, 6Zi (г=--1, 2, п) выберем произвольно Sn - p вариаций, придав им произвольные значения; остальные же р вариаций выразим через первые при помощи ур-ий (186), для чего нужно будет совместно решить относительно желаемых вариаций систему р однородных линейных ур-ий, полученных из (186):

бх 4-

hSx, + yP-

dxi 1 dvi

(193)

Подставив затем найденные р вариаций, вырансенные через Sn-p произвольных вариаций в равенство (192), получим сумму элементарных виртуальных работ сил Ff как однородную, линейную функцию от 3w-р произвольных вариаций. В виду же произвольности этих вариаций придем способом, аналогичным вьппеприведенному, к выводу, что коэф-ты при произвольных вариациях равны нулю. Таким образом получим Зп-р-ур-ий равновесия, связывающих координаты точек системы с компонентами сил Fj, т.е. получим число условий равновесия, равное степени свободы системы, что и обобщает сделанный нами вывод, касавшийся условий равновесия твердого несвободного тела.

Выполнение всех указанных выше действий на практике однако весьма утомительно, вследствие чего применяется еще и следующий метод. Умножив ур-ия (193) соответственно на р множителей Л^, Ag, Я3, Яр, величины которых определяются впоследствии, и сложив эти результаты с ур-ием (192) получаем:

-4-я / 1

+ S(+xg;+...+A,g;)cfe, = 0. (194>

Последнее равенство справедливо при все-возмолных значениях А и для всех возможных перемещений системы. Выберем множители так, чтобы коэф-ты при р первых вариациях, начиная от бх, аннулировались. Тогда в левой части ур-ия (194) останутся только Зп-р вариаций, и притом совершенно произвольных, вследствие чего коэф-ты нри них аннулируются. В конечном итоге следовательно все сводится к тому, что коэф-ты при Зп вариациях в ур-ии (194) равняются нулю, т. е. что

Xi+K, Yi + X,{

(195)

Если исключить из последней системы множители А, то получатся опять Зп-р ур-ий равновесия. Указанный метод нахождения

условий равновесия носит название метода неопределенных множителей (Лагранж). Сравнивая ур-ия (195) и (187), можно сразу же получить компоненты сил реакции:

(196)

До сих пор мы разделяли силы, действующие на систему, на две категории: на силы движущие и силы реакции связей iJ. Можно однако действующие на систему точек силы разделить на другие две категории, а именно: на силы внешние и силы внутренние. Внешними по отношению к данной системе называют силы, к-рые исходят из точек, не входящих в данную систему; внутренними яе силами называются силы, источниками которых являются материальные точки, сами входящие в состав данной систелп.!. Так, если рассматривать систему, состоящую из земли и луны, то силы притяжения солнца будут силами внешними, а силы взаимного притяжения земли и луны- силами внутренними. Если же в состав системы включить также и солнце, то все перечисленные силы будут силами внутренними. Группировка сил на движущие силы и силы реакций не совпадает с группировкою на внутренние и внешние силы, т. к. бывают движупще силы внутренние и внешние, точно так же, как и силы реакции связей бывают внешними и внутренними. Характерной особенностью сил внутренних является то, что они, на основании принципа равенства действия и противодействия, попарно равны и противоположны. Т. к. вследствие этого все внутренние силы во всяком случае взаимно уравновешиваются, то при равновесии системы и все внешние силы долнс-ны между собою взаимно уравновешивать--ся. Последнее предложение находит многочисленные применения при определении законов равновесия нетвердых систем, как напр. жидкостей, газов и т. п.

Динамика системы точек и твердого тела. Для того чтобы обобщить вышеприведенные выводы так, чтобы законы движ;ения материальной точки и законы равновесия системы материальных точек оказались частными случаями более общих выводов, рассмотрим систему п точек, массы которых Шу, mj, m находятся под воздействием следующих связей, Которые могут зависеть также и от времени t\

/iCi, 2/1,1, а'2, ...,л„; 0 = 0 /аСжьШ..Жа, ...,г„; 0 = 0

/р (Жь 2/1, i, 2, ..., ; 0 = oi

Пусть кроме того к точкам системы приложены соответственно силыFxF ..., F. Если прибавить к этим точкам силы инерции -mi i.-тзйг то на основании принципа Д'Аламбера, выраженного формулою (153), точки системы будут находиться в равновесии, вследствие чего мож т быть в свою очередь применен принцип возможных пе-

(197)

ремещений, выраженный равенством (192). Т. о. как синтез обоих принципов получаем:

2(l,--m,a,)rfr, = 0,

(198)

или, что то же самое:

+ (z,-m,)fe,]=0. (198)

Вместо ур-ия (198) имеем также, пользуясь системой ур-ий (195), заменившей, как мы видели, ур-ие (192):

) (г = 1,2. ...,n).(l99)

Последние ур-ия носят название уравнений движения Лагранзка 1-го рода. Умножив Зи ур-ий (199) состветст-венно на 8х^, 6у^, SZf, сложив результаты и приняв во внимание ур-ие (193), получаем снова ур-ие (198) или (198). Исключив величины Xj (j=l, 2, р) из (199), получаем Зп~р линейных ур-ия между проекциями ускорений точек и компонентами движущих сил. Эти ур-ия вместе с р ур-иями связей и определяют однозначно движения точек системы. Ур-ие (198) удовлетворяется любой системе й возможных элементарных перемещений 6г^, если последние удовлетворяют системе ур-ий (193). Если же рассматривать систему элементарных перемещений dr, которые в действительности имеют место за промежуток времени df, то они должны удовлетворять системе vp-ий:

+ ldz + -dt==0 (/= 1, 2, п), (200) отлиющейся от ур-ий (193) тем, что она содержит еще и члены dt. Вследствие этого истинные элементарные перемещения dr; не совпадают в общем с возможньпди элементарными перемещениями 6г^ системы. Таким образом в обшем нельзя смешивать перемещения dr и rfr. Если же ур-ия связей (197) не содержат t в явной форме, то

члены dt в ур-ии (200) исчезают, а вместе с тем исчезает и различие между действительными и возмояными перемещениями системы. В последнем случае можно следовательно писать вместо (198) также: п

2(F,-Wia,)dr,=0. (201)

Т. к. на основании (125)

2m, idri= dLi,

(202)

то имеем из (201):

{Fidr,)dL; = dL, (203) 1 1

п

где jL= 2 А т. е. в этом частном случае

cyMJia элементарных работ всех движущих сил равняется сумме диференциалов живых сил точек системы. Интегрируя (203) в пределах от 1 до ti, получаем, что полная работа всех движущих сил за какой-нибудь промежуток времени равняется изменению суммы кинетич. энергии всех точек системы за тот же промежутоквремени. Это предложение имеет место, если ур-ия связей не содержат tb явной форме, в противном же случае сумма работ сил реакций при действительных перемещениях точек системы не равняется нулю, поэтому надлежит учесть и работу последних сил. В общем среди движущих сил Fi могут быть как потенциальные, так и непотенциальные силы. Сумма элементарных работ первых сил равняется но (133) -dU, где U = Uj, а Uj-силовые функции, соответствующие имеющимся потерщиальным силам; сумма элементарных работ непотенциальных сил:

Fdr.dA, fe=i

(204)

где jF -непотенциальные силы, число которых V. Тогда имеем:

Fi-dri=-dU + dA,

(205)

или по (203):

dL = -dU +dA, d(L -Ь С7) = d. (206)

Так как кинетич. энергия L системы зависит от скоростей точек и так как эти скорости- понятия относительные, то и кинетич. энергия системы точек есть также величина относительная, зависящая от состояния системы отсчета. Допустим, что имеются две системы отсчета: одна с началом О, не связанным с данной системой точек, и другая с началом О', неподвижно связанны.м с системой точек. Пусть Vi и г< (фиг. 55) суть радиусы-векторы, определяющие положение точки Ai по отношению к систелтам О и О' соответственно, а г -радиус-вектор, определяющий положение точки О' по отношению к системе с началом О. Тогда имеем:

* . = *; + о.

И.ТШ, что то же самое,

- cci -f Жо; Vi = yi -h l/o; 2i = 2- + 2o.

Беря производные по времени от последних равенств и обозначая производные точкою над соответствующей переменной, имеем:

XiXi+x,; yi-yi+Ы 2i = ii + 2\. (207)

Фиг. 55.

Для кинетической энергии L системы точек, принимая во внимание (26):

L = lmiVf = I (i? -f } + zf) = 1.1

= lniiiiii + + (yi + ky+ Oi+zoT-] = 1

n n n

где

V = \x + y-t- 22 и г'о=+ У + z

суть линейные скорости точки А^ по отношению к системе О' и точки О' по отношению к системе О соответственно. Пусть далее координаты центра масс системы точек по отношению к системе отсчета с началом О' будут X, у, Z. Тогда на основании (171): x-miniiXi; у-mimiyl;

Если точка О' совпадает как раз с центром масс, TQ так как х=0, у=0, z=0, получим:

2 ii = 0; 2 iVi = О' S °= и следовательно

2w,<c;. = 0; 2гЙ = 0; miZ=0.

В этом случае следовательно три последних члена левой части равенства (208) равны нулю, так что получаем:

L = 4 VI 2 +12 i?- (208) 1 1

Т. о. кинетическая энергия системы точек рйвна сумме кинетической энергии центра масс, если в нем сосредоточить массу всей системы, и кинетической энергии системы в ее движении относительно системы отсчета, имеющей начало в центре масс.

Основной динамический закон движения, выраженный ур-ием (198), допускает еще ряд других формулировок, имеющих в конечном итоге один и тот же физич. смысл. К числу последних принадлежит так наз. принцип наименьшего действия, или принцип Гамильутона. Так как ур-ие (198) справедливо для любого момента времени, то, умножив ур-ие на df и проинтегрировав результат в пределах от <i до <2, получим:

и

(209>

где индексы г для упрощения опущены. В последнем ур-ии следует рассматривать как функции времени не только координаты ж^, yi,Zi, но и вариации 6xi,6yi,6zi, что вытекает из следующих соображений. Допустим, что все координаты точек зависят не только от t, но еще и от цек-рого параметра г]. Опре-

деленному значению ri соответствует тогда определенное движение точки Л^; значению же 1?+ ? соответствует нек-рое бесконечно близкое соседнее движение, к-рое конечно в общем не удовлетворяет уравнению данного движения. Действия d и 6, соответствующие изменениям величин по времени и по параметру, независимы друг от друга, вследствие чего можно писать:

6х

,dx dt

(210)

причем вариации = 1, будучи в любой момент произвольными, должны однако удовлетворять условиям (193). Применяя полученную ф-лу (210), имеем, интегрируя по частям:

-f dill

ddx dt

Если предположить, что координат равны нулю при t = tn t

dx dT

вариации всех h, то

oxI =0, и тогда имеем из (211): t

tl . t

С другой стороны, по (205) имеем:

iXSx + Ytfy + Z6z) = --6U + 6A. (212) Подставляя (211) и (212) в (209), получаем:

j dt {SH + 6A) = О, (213)

где H=L- и. Величина Я называется к и-нетическим потенциалом, или ла-гранжевой функцией системы.. Равенство (213) и выражает принцип Гамильтона. Т. к. формулировка этого принципа не зависит от системы координат и т. к. кинетич. потенциал Н и работа непотенциальных сил А встречаются во многих областях физики, то применение этого принципа встречается очень часто при исследовании вопросов не только М. т., но и электродинамики, термодинамики и т. п. Очень часто положение точек системы определяется не при помощи прямолинейных ортогональных координат, а при помощи других координат: полярных, цилиндрических и т. д. (см. Координаты), к-рые удобнее применять при данных условиях двилсения. Как и в приведенных выще случаях, число таких координат, к-рые обозначим через д^, q, должно равняться степени свободы системы, если они независимы друг от друга. Координаты же Xi, Vi, Zi суть тогда определенные функции от qx, qi,..., а если связи зависят от времени, то и в явной форме от t:

Xi-=Xiiqx, qi,...;t)\

У/==У.(91, ?а,...;0 > (214)

Ziiii((}x,q2,...]t))

Если связи от времени не зависят, то, как видно из (214), полные производные их по f, т. е. Vg, Vy, Vg - однородные линейные

функции от , коэф-ты при которых могут

содержать qj. Так как, с другой стороны, вариации 6xi, ду1, 6zi-однородные линейные фу]п<ции от 6qj. а SA-линейная однородная функция от Sxi, 6yi, 8zi, то 8А м. б. представлена в следующем виде:

rf4 = 0i%-Ьба'а + Мдв-Ь..-, (215) причем 6А может содержать элементарные возможные работы как потенциальных, так и непотенциальных внешних сил. Гак как величины играют ту же роль, что и компоненты Xi, Yi, Zi в ф-ле (212), то они называются обобщенными компонентами сил.

Нетрудно усмотреть, что кинетич. потенциал Н представляет собой в рассматриваемом случае ф-ию 2-й степени от производных qj, коэф-ты к-рых суть ф-ии от q, а воа.можно и от Т. к. при вариировании координат q время t не меняется, то

mfrSqx + frSq,,.,- . ая . , дН . ,

agj ! * .(216)

Из (216) имеем, принимая во внимание, что

fSqjdt= ri-dt J dqj J dqf dt

(-1.2.-). (8П)

так как при f = и f = все вариации дд равны нулю. Подставив значения (216) в (213), получим, принимаяво внимание (217). а также и то, что Sqj независимы друг от друга:

(218)

Последние ур-ия называются уравнениями движения Лагранжа 2-го рода. В качестве примера рассмотрим движение свободной материальной точки, положение к-рой определяется цилиндрич. координатами г, <р, z. Из (215) имеем:

6А в^бг + 02<Р + 03(219) При отсутствии потенциальной энергии

Так как

х = г cos 9? и 2/ = г sin 9>,

= (г cos 93 - г sin <р-(р) + (г sin q> + r cosy qjy

-\-z=r- +rq z\

следовательно

Отсюда получаем, сообразно (218):

д(р дН dz

01=., {тг) - тг<р-

(220)

Oz = (жг>)

дз=},(ш'г)

Выше мы разделяли все силы, действующие на систему материальных точек, находящуюся в покое, на силы внутренние и силы внешние. Аналогичное подразделение можно сделать и в отношении сил, действующих на дви->кущуюся систему, причем отмеченное выше основное свойство внутренних сил сохраняется и в данном случае. Обозначая внешние силы через Ф^, имеем, применяя к движущейся системе принцип Д'Аламбера, на основании ур-ий (179):

п

У.{Фi-miai)= 0, (220)

2[ -.-(Фг-ВД)] = 0, (220 ) 1

т. е. во время движения системы точек силы внешние и силы инерции в любой момент времени взаимно уравновешиваются. Ур-ия (220 и 220 ) применимы как к твердым, так равн ) и к нетвердым системам точек, как то: к газу, жидкости ИТ. п. ив частности к твердым телам. Т. к. из (171) следует, что

т

= S.S=2* - (221)

где W = 2 -масса всей системы точек,то.

вставляя (221) в (220), получаем:

dirn

т

(222)

т. е. что ц. т. системы материальных точек движется так, как будто масса всех точек системы собрана в нем и как будто все внешние силы, действующие на систему, прилонее-ны непосредственно к этой точке. Отсюда видно, что на движение центра тяжести системы внутренние силы никакого влияния не оказывают. Из (220) имеем также:

2т,г;, = 2Ф^, (223)

т.е. производная по времени от суммы количеств движения точек равняется сумме (векторной) внешних сил, действующих на систему. Если все внешние силы равны О или п

ели 2 * = О, то из (223) имеем: 1

п

miVi-= Const.

Т. о., если Ф^=0,то сумма количеств дви-1

жения точек системы, называющаяся также результирующим кол и ч е с т в о м движения, остается во время движения без изменения. Особенное значение имеет последнее предложение при исследовании явления удара (см. Удар). При^ = О имеем также из (222):

= Ло = 0, . (224)

т. е. если на систему точек не действуют никакие внешние силы или если действуют силы, сумма к-рых равняется нулю, то центр тяжести системы движется прямолинейно и равномерно. Из (220 ) имеем далее:

или, так как [v v] = О,

:[г^т^ь^]=[Г1Ф^], (225)

т. е. производная по времени от суммы моментов количеств движения точек системы по отношению к какой-либо точке равняется сумме моментов всех внешних сил по отношению к той же точке. Сумма моментов количеств движения точек называется также главным моментом количества движения системы. Если в частности имеетсИ свободное твердое тело, причем внешние силы Ф^ даны, то уравнения (220) и (220 ) вполне определяют движение тела, т. к. число этих ур-ий, равное 6, соответствует 6 степеням свободы тела. Допустим однако, что тело, к к-рому приложены данные силы, не свободно, а имеет одну неподвижную ось врашения, к-рую мылримем за ось Oz. Взяв на этой прямой произвольную точку О', приведем к ней всю систему сил Ф^, так что получится одна равнодействующая сила Ф и пара момента М. Аналогичным образом можно к той же точке привести и неизвестные силы реакции оси, получив силу Ф' и момент Ж'. Из всех шести ур-ий (220) и (220 ) только последнее не будет содержать компонент неизвестных сил реакции, а именно:

S - Vi = (226)

а следовательно только оно и определяет движение тела, в соответствии с одной степенью свободы его. Параметром, определяющим положение тела, служит угол поворота (р, который образует плоскость в теле, проходящую через Oz, с плоскостью, неподвижной в пространстве и проходящей через ту же ось Oz. Обозначая расстояние точки (ж^, 2/, Zi) до оси Oz через е,-, имеем:

Xi Qicos (р; yiQiSintp; (227)

QiSin<p-i>; = Qicos(p-r, (228) = - Qi cos V 9> ~ QiSimp (p;

dli = - sin (p-(p-i- Qi cos (p (p. (229)

Вставляя равенства (227) и (228) в (226) и принимая во внимание, что угловое ускорение <р постоянно для всех точек тела, получаем:

(230)

тде знак заменен знаком J в виду того,

что суммирование произведено по всем точкам объема тела, dm представляет массу элемента объема, находящегося на расстоянии Q ОТ ОСИ Oz. Величина

4= Г dm (231)

называется моментом инерции тела относительно оси Oz (см. Момент инерции). Т. о., обозначив угловое ускорение через , имеем:

в-1, = М,. (232)

Полученная формула (232) аналогична формуле (107) прямолинейн. движения, причем вместо массы здесь имеется момент инерции, вместо линейного ускорения-ускорение угловое, а вместо силы-вращающий :,10мент внешних сил. Интегрирование ур-ия (232) производится точно таким же способом, как и при прямолинейном движении. Кинетич. энергия тела получается в рассматриваемом случае из следующего общего выражения:

(V) (F)

из которого, воспользовавшись формула-тии (228) и обозначив угловую скорость через со, имеем:

Если в какой-нибудь момент кинетич. .энергия тела равна Li = IiCol, а в момент

tz равна 1/2 = 2 -201, то на основании закона

живой силы, выраженного ур-ием [(125), имеем:

T = ll,col-ll,c

2 (235)

Из шести координатных ур-ий (220 и 220 ) остались еще неиспользованными пять ур-ий, определяющие реакции оси, а именно:

Ф'==т^щ-Ф, (236)

м; = 2 (i - ® - }

которые и определяют Ж' = М' + 31 у и Ф'. Если в частности все силы Ф равны пулю, то из (232) имеем:

0 = 0 и = ft> = Const. (238)

В этом случае реакции оси определяются ур-иями:

(237)

dt2 dt2

(239)

Вставляя в Ф'х^Щ значения * и ~ из (229), получим:

(240)

или на основании (171):

Фх = - 4fXo 2 = - 2 . (241) Фу = - VVo 2 = - Уо 2 4 Т.к. проекции центробежной силы инерции точки, масса которой т, по осям координат суть а)-х т и соу т, то согласно (241) результирующая реакция связи Ф', противоположна центробежной силе инерции центра тяжести, в котором сосредоточена вся масса тела и который вращается с угловой скоростью со. Если ось вращения проходит через центр тяжести тела, то, 1шк это видно из (241), Ф'= О, т. е. в этом случае результирующая сила реакции оси равна нулю, но вращающие моменты М' и My в общем случае не равны нулю:

ч

(242)

(243)

т. Э. т. XIII.

Т. К. далее = О, то из (229) имеем:

Вставляя значения (243) в (242), имеем:

М;= 2* = ?2**--2i= yf\.(2U) My=-miZiXi(f= 2bXiZi=-Ixz<P J

где Jyg и Ig-т. наз. центробежные моменты инерции, Т. о. даже в рассматриваемом частном случае для того, чтобц осуществить неподвижную ось вращения тела, иулшо будет приложить два вращающих момента -М^ и -fM; если же ось сделать свободной, то, несмотря на отсутствие движущих сил, ось вращения все же неподвижной не останется, а будет перемещаться определенньш образом в пространстве. Лишь если центробежные моменты инерции тела

/а-г и будут К ТОМу Жб раВНЫ Н^ЛЮ, ось

останется неподвюкной в пространстве и без всякой поддержки. Такая ось вращения тела называется свободной, или перманентной.

Графостатика. Помимо вышеприведенных методов определения условий равновесия системы сил при помощи составления и решения определенного числа ур-ий, т. е. помимо методов аналитических, ши- роко применяются, в особенности при решении практических задач статики, методы графические, составляющие предмет изучения графической статики, или графостатики. Каждый из этих методов имеет свои преимущества и свои недостатки. Аналитич. метод дает в общем более точные результаты, достигаемые однако путем сложных и утомительных вычислений, связанных с составлением и решением ур-ий, выражающих условия равновесия. Графический метод, наоборот, давая более быстрые результаты и отличаясь легкостью усвоения и запоминания, дает однако менее точные результаты. Во всех тех случаях, когда особой точности результатов не требуется либо когда в сложных случаях приходится делать допущения, понижающие точность аналитич, методов, графич. мето-

ды обладают нрсомнрнными преимуществами перед аналитическими. В посл<Днее время графич. методы находят применение также в области динамики, составляя прс^дмет изучения графической динамики. Однако во многих случаях П1)именение одних лишь графических методов не является достаточным для решения поставленных задач статики, так что п[Шходится применять смешанные граф о-аналитичес кие методы. В особенности это имеет место при определении неизвестных усилий в так наз. статически неопределимых системах (см. Фермы), когда помимо обии1Х ур-ий статики н( обходимо принимать во внимание еще и упругие изменения системы. Развитие гра-фсстатики связано с развитием т. паз. про-ектив! ой геометрии. Основными методами для графостатики являются постро ния силового многоугольника и т. наз. веревочного многоугольчтка (см.).

Если имеются две силы и Fg,приложенные к лвум различным точкам / и (фиг. 56) и лежащие в одной и той же плоскости, линии действия к-рых пересекаются в некоторой точке 111, находящейся вне пред(лов чертежа, то прямое применение п[)иведен-ного метода полного решения не дает. В самом деле: построив от какой-нибудь произвольной точки О силовой мн-к 012, так что -* ->

0J = Fi и 12= Fz, получим равнодействую-->

щуюР=02 лишьпо величине и направлению; линия же действия F остается неизвестной. Для определ'чпя положения последней приложим к точкам 1 и II две равные и прямо противоположные силы Qi п Q, так что Qi = ~Q2- Складывая по правилу параллелограмма попарно силы F и Qi, Fg и Q, получим силы Bi и Bz, однов1)еменное действие к-рых точно такое же, как и действие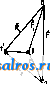

Фиг. 56.

сил Fj и Fj. Если силы Qi и достаточно велики, то, продолжив линии действия JS, и можно получить точку пересеч ния III, находящуюся в пределах чертежа и через которую очевидно проходит искомая линия действия Fпараллельно найденному направлению 02. От той же точки О можно построить д])угой силовой мн-к 012 соответственно силам jBj и jb2.TaK4ToOi = J?i и 12=В.,

причем очевидно, что И' = Qx и 11 = Qg.

Отрезки 02 и 11 представляют собой диагонали четырехугольника 0121О, точно так же, как отрезки III III и III суть диагонали четырехугольника 1III II 11Г1. Нетрудно также заметить, что между этими четырехугольниками существует взаимно обратное соответствие, к-рое состоит в том, что каждой стороне или диагонали одного

четырехугольника соответствует параллельная ей сторона или диагональ другого четырехугольника, а каждой точке, в которой сходятся три направления одного четырех-угольни1{а, соответствует тр-к с параллельными этим направлениям сторонами в другом четы[)ехугольнике. Так например точке соответствует тр-к 121, а точке I соответствует тр-к II 1 ПГ. Во взаимно обратном соответствии этих фигур и проявляется тесная связь, сун^ествующая М'-жду построениями графостатики и проективной геометрии. Таким образом, чтобы полностью получить равнодействующую F. достаточно поступить след, образом: пост{)оив силовой мн-к 012, возьмем произвольную точку С,.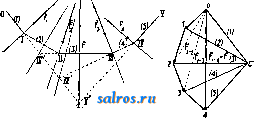

Фиг. 5 7.

называемую полюсом, и соединим ее со вс( ми вершинами силового мн-ка прямыми, или лучами, СО, С1, С2. Проведя далее прямые: 01П СО до пересечения в точке 1 с лини й действия Fi; IIIWCl до пересе ения в точке II с линией д-йствия Fa и II III 11 С2, получим мн-к О 1 II III, крайние стороны коТо~>ого пересекаются в течке 111, через к-)ую проходит линия действия силы F=02. Мн-к 01 11 111 называется нитяным, или веревочным.

Приведенное построение можно распространить и на более общий случлй. Допустим, имеется плоская система п сходяпщх-ся или не сходящихся сил F, Fa, F . Пусть например w = 4 (фиг. 57). Для сил Fi и Fa найдем вышеприведенным способом все элементы, определяющие их равнодействующую Fi2, т. е. вел1шину, направление и линию действия последней; взяв затем Fia и F3, аналогичным об[)азом найдем все элементы их равнодействующей Fi3 и т. д. Все построение очевидно сведется к следующему. Построив силовой мн-к 01234 и взяв п1)оизвольный полюс С, соединим его лучами СО, С1, ... со всеми вер-ШИ1ШМИ силового мн-ка. Затем из произвольной точки О проведем: прямую 01 параллельно 1-му лучу СО до пересечения в точке I с ли!П1вй действия силы Fi, прялгую I II параллельно 2-му лучу до пересечения в точке и с линией действия силы Fa и т. д. Полученный так. обр. нитяной мн-к вместе с построенным силовым мп-ком дает возможность определить равнодействующие как всех данных сил, так и определенной группы их. Так, для получения линии действия равнодействующей F сил Fj и Fg достаточно продолжить крайние стороны нитяного мн-ка, соответствующие этой части фигуры, т. е. стороны (1) и (5) до их взаимного пересечения в точке III, и провести через III прямую, параллельную 02. Be-