• Что такое фактурная штукатурка
• Выбираем сухие строительные смеси
• Преимущества напряженного железобетона
• Что влияет на выбор кровельного материала
• В чем преимущество пробковых полов

при этом положительными считаются те сжимающие напряжения а и трансверсаль-ные напряжения г, к-рые вращают элемент рассматриваемого тела по направлению часовой стрелки. Распределение напрян^ений вдоль сечения происходит приближенно линейно по закону трапеции. Для произвольной точки с координатами xviy тогда будет иметь силу следующее выражение с обозначениями по фиг,* 7:

а равновесие элемента рассматриваемого тела у возд>чпной и водной сторон требует

Фиг. 8.

Фиг 9.

удовлетворения следующих ур-ий: а) у воздушной стороны П. (фиг. 8):

+ Ту, tg щ = О,

или

или

fyi = - ctg ч<1 = - т^-г; = ri ctg Щ

(9) (9)

(10)

(10)

молгно также написать:

и т. к. Г^,1 = -Та б) у водной стороны (фиг. 9):

yw = (<У - УоУ) ctg грго = - xw

(11)

<yw = УоУ^ iw - УоУ) Ctg2 у,. (12) где у о-уд. в. воды. Краевые напряжения oi я в горизонтальных сечениях м, б. определены из внешних сил. Если в произвольном месте массивнойпло-тпны известны

Фиг. 1

напряжения а^, Оу,х, то оба главных напряжения будут:

Ох,-, = \ \.а^ Л-а.у± i/(a, - а^) -f- 4], (13) а главные направления будут характери-

зоваться следующим уравнепиел!

Наибольшие и наименьшие значения напряжений а^., Оу, X лежат в контуре массива. Главные направления совпадают с омьшае-мыми водой и воздухом боковыми поверхностями П остальные главные направления перпендикулярны к ним. Направления главных напряжений в сечении массива П. характеризуются траекториями (фиг. 10), которые начинаются перпендикулярами у одной стороны контура П. и приближаются асимптотически к его другой стороне. Вдоль траекторий трансверсальных напряжений не существует. Вырежем мысленно (фиг. 11) из тела плотины очень маленькую призму длиною= 1 уводной стороны, причем одна боковая грань лежит в контуре, вторая - перпендикулярна к ней, а третья горизонтальна; первые 2 боковые грани перпендикулярны к главным направлениям. Равновесие призмы требует, чтобы сумма моментов всех сил, действующих вокруг произвольной точки (например вокруг точки О), была равна нулю:

Фиг. 11.

Р 2 cos V,

+ J.sin v,.-F-2 = 0. (15)

При длине горизонтальной стороны сечения призмы, равной единице, будем иметь еще следующие равенства:

V = о -1; Т = т 1; Р =-уо-Ь-1-аов tp \

N = 1 sin y>w

где ori-главное нормальное напряжение в контуре П.; у^к-давление водына высоте горизонтального сечения. Подставляя эти величины в ур-ие (15), получим:

у oh cos2 V + ai sin2 <г, = 0, (16)

или

sin 2 Va,

-у oh ctg2

(16)

<wi = yoh. (17)

Чтобы у водной стороны П, не было растягивающих напряжений, линия давлений не только должна проходить внутри ядра, но и одновременно должна быть настолько отдалена от расположенного к воздушной стороне края ядра, чтобы было соблюдено следующее условие:.

ftc > У oh cos2 у}, (18)

т. к, только в этом случав а^л > О, и следовательно напряжения-сжимающие. По Ке-лену главные напряжения получаются равновеликими независимо от направления сечений массива П. Когда оба главных напряжения ffi ио-г по ф-ле (13) положиуельны (сжимающие напряжения), то трансверсальные напряжения можно игнорировать. Редуцированное главное напряжение (напряжение, которое вызывает те же деформации, что ц

плотины

главные напряжения и о^) будет

и

(19)

У водной стороны главные напряжения будут:

<i = tr,ci. о^==Уо, (20)

так что:

wiped.-rci-iiroh. (200

Подставляя в последнюю ф-лу величину ai, из ф-лы (16), получим:

Wa. = s-nS-?o(ctgV.+ ). (21)

Величина т в ф-лах означает коэф. Пуассона, к-рый для бетона в зависимости от его состава варьирует в пределах 5-12.

При проектировании П. намечают профиль и определяют все усилия, действую-п^ие на участок П. длиною в 1 ж (как было указано выше), после чего проверяют дей-

Фиг. 13.

ствующие в рассматриваемом элементе П. напряжения, к-рые нигде не должны превосходить допускаемых, в противном случае намечают новый профиль, проверяя опять его до получения вполне удовлетворительных результатов. Проверку намеченного профиля делают как при наполненном, так и при опорожненном водоеме. Для средних высот наиболее экономичньпк! профилем П. будет треугольный с вертикальной гранью, обрашенной к напорной воде, и с вершиной, расположенной на уровне наивысшего горизонта воды (фиг. 12). При таком профиле у водной стороны не будет растягивающих напряжений, если при заполненном водоеме краевое напряжение будет равно нулю. Равнодействующая всех сил должна проходить в ядре сечения как при заполненном, так и опорожненном водоеме. При уд. в.у^ каменной кладки П. вес участка ее в 1 л длины

будет равен у^-у- Ширина Ъ подошвы П,

определится из выражения:

bh Ь TI7- h

У-г^-3--В = Уо <22)

где ТГ-давление воды. Решая ур-ие (22) в отношении Ъ, получим:

Определив треугольный профиль П., уширяют гребень ее соответственно потребностям; при сообщениях через П. ширина гребня делается 3-6 м. Чтобы начать с какого-либо профиля П., берут предварительно Ь = 0,7 h иу = 2,4 т/м^. При к>ЪО м принимают b > 0,7 Л. Со стороны воды придают

(23)

П. скат, с заложением а? = wb = Ч- /г. По Липку (см. обозначения на фиг. 13);

Т. к. всякое наклонение водной стороны П. уменьшает стабильность П., то нек-рые авторы рекомендуют отказаться от всякого уклона водной стороны П. и делать водную грань вертикальной. Если с водной стороны плотина имеет наклонную грань, то для предотвращения растягивающих напряжений недостаточно уже одного условия, чтобы равнодействующая проходила в ядре сечения, но (как выше было указано) необходимо, чтобы одновременно было соблюдено условие (18), По Шокличу в сторону воды потребуется большее уширение П чем указано выше, если стена П. достигнет высоты, при к-роЙ у водной стороны допускаемое напряжение будет превзойдено под влиянием веса массива П. при опорожненном водоеме. Если линия давлений при опорожненном водоеме совпадает с ядровой линией, ближайшей к водной стороне П., то напряжения распределятся по тр-ку, и краевые напряжения с воздушной стороны будут равны нулю. С водной стороны краевое напряжение определится по ф-ле:

w-yJ, (25)

где Уда выражается в m/jn, а h-глубина расположения рассматриваемого шва в ж (считая от гребня П.), Начиная от глубины

доп.

(26)

допускаемое напряжение а^аои. было бы превзойдено, вследствие чего, начиная с этой глубины, П. должна быть с ее водной стороны более уширена. Это мероприятие однако может иметь

место лишь при очень высоких П. Каммюл лер дает для определения краевых напряжений в швах следующие ф-лы (фиг. 14). а) Для низовой стороны П.(основные напряжения):

i=fe[l

Фиг. 14.

(tga-t-tg)

tga-btg/S

(l-tgatg/3)

aHl + tga)

;(27)

~ COSa

6) Для верховой стороны П. (основные напряжения):

tga-

(tg -Mg,).(l-2tg tg/J-cT;=p-T tg j8;

>;(28)

-T tg; T = (p-(7.;)tg;5 здесь p - давление воды, т - напряжение сдвига. Чтобы избегнуть растягивающих краевых напряжений, необходимо условие: (r;>psin2/3. (29)

Для массивных П. последнее условие в виду малости угла практич. значения не имеет,

однако оно существенно для опор арочных П. в) Добавочные напряжения от уширенной части гребня П. выражаются ур-иями:

, (а--о)-я 6 \

(tga-t-tg/S)2/i2

(tga + tgS)2h2 j

где к-величина нагрузки от уширенной части гребня П., d-расстояние силы К от оси ж-ов (фиг. 14),

п - tgo-at!?/?,. а - - п,

знак плюс означает растяжение, знак минус-сжатие, г) Добавочное напряжение от

давления воды при повышении высоты плотины и уровня воды над вершиной основного тр-ка П. (фиг. 14). Если уровень воды на величину Afe tg а превышает вершину основного тр-ка П., то равное по всей высоте добавочное давление выразится величиной Др = = Ah -у^, адобавоч-

.2,80.

-то --J

Фиг. 15.

ные напряжения от повьппенного уровня поды выражаются следующими равенствами:

- (tW I- 3 + tg (2 tg а - tg )] I 3

<=aWl3-tg(4tga-ftgl ) Напряжения независимы от высоты плоти-

SepeSovHbiu многоуг. со6ст& веса плотимы

Чг...

/ л^ч

h(tga + tg/3)2 V Ь.)

(3Z)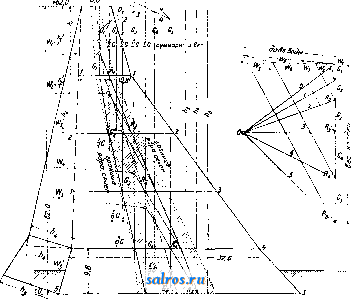

Фиг. 16.

ны. д) Добавочные напряжения от давления ледяного покрова водоема определяются из следующих уравнений:

fl(tga+tg)2

где И-горизонтальное давление льда на расстоянии А/г от вершины П. Во вновь сооружаемых П. вершину основного тр-ка располагают на высоте уровня воды, вследствие чего расчет на добавочное давление воды по (г) обыкновенно отпадает. По Кам-мюллеру давление льда неопасно для П.,. а давление от уширенной части гребня П. улучшает статич, состояние ее.

Действующие в П. напряжения определяют наилучшим образом графическим пу~ тем. На фиг. 15 граф. расчет П., а на фиг. 1в статич. расчет массивной П. с построением кривой давления. Для построения линии давлений разделяют профиль П. на части горизонтальными линиями (швами), расположенные друг от друга на расстояниях, соответствующих 5 л*; для каждого шва затем определяют равнодействующую всех усилий, действующих на рассматриваемый шов как при наполненном, так и опорожненном водоеме; соединение во швах точек приложения равнодействующих сил дает искомую, кривую давлений, к-рая должна всюду проходить внутри ядра сечения. Чтобы не было скольжения в горизонтальных плоскостях сечений, угол между равнодействующей и вертикалью не д. б. более 37°. Все расчеты должны основываться на допускаемом напряжении раствора кладки, так как это напряжение ниже такового для камня или кирпича. Наибольшее допускаемое краевое-напряжение обыкновенно принималось равным -г- временного сопротивления каменной кладки П., причем это допускаемое-напряжение не должно превышать 12-16-кг1(м^. Ширина гребня П. и высота П. над высшим ординаром воды зависит от глубины /г^, воды в водоеме. По Ре-боку: а) высота П. над высшим ординаром воды в м:

1 = Г|+ 0,3л1; (33).

б) ширина гребня П. в л :

Ьк= -Ы,8 Л1 = hi-Ь 1,5 ж. (34)

По Круньола (Crugnola) ширина гребня П. при /г„=5-50л* варьирует в пределах 1,70- 4,75 Л1, а высота П. над высшим ординаром воды при том же значении hy,-в пределах 0,50-3,50 м. По Кранцу при fe=54-50 м величина = =2,00-г5,00 м, а величина fej=0,50-1-3,50 JW. В табл. 1 приводятся сравнительные расчетные предположения с учетом подфундаментного напора и без такового, соответ---. ственные этим предположениям вершинные углы (фиг. 14) основного треугольника П. (при удельном весе каменного материала. у=2,3 т/м^) и сравнительный расход ка-. менного материала для плотины.

Т а G л. 1 .-С 1> а в н п т f л ь н ы е данные о в е i> ш и н н ы х углах П. и расходе к а м е н-

ного материала.

В приведенных в табл. 1 формулах величина п означает подпорный коэфициент. Против скольжения основывают П. на прочном фундаменте с принятием указанных вьппе мер или заделывают (в нижней части) в скалу: фундамент П, закладывается на материке i 2. Технические условия проектирования гравитационных П. В отношении очертания П, в плане по франц. технич. условиям признается рациональным придание П. криволинейного очертания лишь при длине П. более 250 л* и при наличии соответствующего очертания долины в плане и профиле. Герм, практика придерживается тех же условий, американская же допускает искривление направления П. лишь в том случае, когда это оказывается выгодным в' экономич. отношении. В отношении поперечного профиля П. франц. технич. условия рекомендуют простой треугольный профиль, избегая отсыпей с верховой стороны. В Америке допускают для воздушной грани 2-3 перелома. В отношении *°-ных явлений по франц. техническим условиям принимают меры путем возведения сооружений отдельными чередующимися секциями, отделяемыми друг от друга Г-ными швами, перекрываемыми непроницаемым и эластичным материалом. Расстояние между этими швами берется 15-30 ж. Д.пя увеличения водоне-

проницаемости шва, помимо применения изогнутой по дуге круга медной пластинки, оставляют в месте расположения шва вертикальную шахту сечением около 1 м^, заполняемую впоследствии раствором под давлением. Для обеспечения П. от давления фильтрационной воды снизу франц, технич. условия рекомендуют устройство защитной шпоры, впрессовывание в грунт цемента, применение дренажа. Для осмотра плотины сооружают колодцы и галлереи. Напорную грань плотины покрывают цементом. В частях, соседних с лицевой гранью, применяют раствор с ббльшим содержанием цемента. В Италии применяют дренаж, в то время как в испанских и швейцарских П. тело П. обыкновенно не дренируют, вследствие чего в расчет вводят полное противодавление фильтрационной воды; низовой грани придают уклон в 0,80-0,85. В америк. П., снабженных почти всегда дренажной системой, этот уклон равен 0,70-0,75. В отношении внешних сил учет ведется различный. Во Франции плотины рассчитьшают только на вес кладки и горизонтальное давление воды без учета подфундаментного напора воды; последний принимается в соображение, когда это требуется местными условиями. По итальянским технич. условиям принимается в расчет давление снизу, равное у верховой

грани туок, где т есть коэф., варьирующий в пределах от 0,33 до 1,0 при высоте П. 25-50 м, причем.при наличии хорошего дренажа и при криволинейном расположении П. в плане указанные числа для величины ж м. б. уменьшены. В Испании и Швейцарии принимается полное противодавление фильтрационной воды. В Америке коэф-т т= 0,25-1-0,30. Давление ледяного покрова по етальянским технич. условиям принимается в 5-25 min. м при высоте 800-1 ООО м над уровнем моря. В Германии давление льда не учитывается, а в Америке вводится в расчет лишь для водоудержательных П., служащих целям водоснабжения. В тех случаях, когда тело П. ослаблено большим количеством отверстий водоспусков и дренажных галлерей, это обстоятельство д. б. принято во внимание при расчетах. Что касается напряжений, то по франц. технич. условиям наибольший допуск напряжения на сжатие принимается в Ve-/ю временного сопротивления, которое выявляется опытным путем. Растягивающие усилия нигде не допу-

770 780 790 800 810 820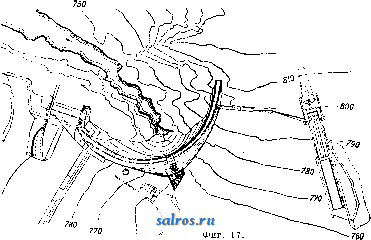

дуют устройство шпоры, в Америке шпоры устраивают всегда, доводя их иногда до глубины 30 Jit, а для уплотнения основания цементируют его посредством нагнетания цемента в ряд предварительно пробуравленных скважин. Особое внимание обращают на сопряжение П. со склонами тальвега, причем применяют обделку уступами по предварительном удалении верхнего слоя по всей ширине профиля, пока не будет достигнута плотная скала хорошего качества, и выбирают небольшую нишу для ядра П. Склоны тальвега в местах примыкания П. обрабатывают так же, как и основание под П.

3. Сводчатые П. Когда перегораживают узкие глубокие в скалистых берегах расположенные ущелья, то является целесообразным сооружать в этих местах плотины в виде одного монолитного свода (фиг. 17 и 18). Сводчатые плотины рассчитываются в наст, время в предполон^ении, что часть давления воды воспринимается горизонтальными дуговыми полосами

- 820

скаются. Рекомендуется построение кривых равного наибольшего сжатия, кривых наи-большего скалывающего напряжения и кривых траекторий главн. напряжений. Итальянские и немецкие нормы близки к французским. Для устранения возможности появления растягивающих напряжений при опорожненном водоеме напорной грани придают небольшой уклон (~0,05). Америк, руководства дополняются условиями, чтобы отношение суммы горизонтальных сил к сумме вертикальных не было > 0,75 (из условия сдвига) и чтобы угол, составляемый воздушной гранью с горизонтом, был 45°. В отношении подготовки основания по франц. технич. условиям д. б. приняты все меры к тому, чтобы обеспечить водонепроницаемость основания (осмотр и подготовка опорных поверхностей, заделка скважин и другие мероприятия). Итальянок, технич. условия обусловливают помимо принятия общих уплотняющих основание мер устройство у напорной грани шпоры в виде траншеи шириной 2-6 м и глубиной 3-9 м, заполняемой бетоном. Герм, нормы также рекомен-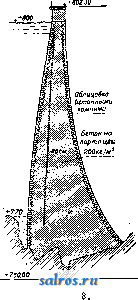

Фиг. 1

свода, опирающимися на береговые .скалистые откосы, остальная же часть давления воды воспринимается вертикальными опорными полосами свода, передающими давление на основание плотины. Распределение давления воды на опорные и дуговые полосы делают с таким расчетом, чтобы общая обеим полосам точка имела одинаковое перемещение как по отношению к дуговой полосе, так и к опорной. По предложению Ергенсена (L. R. Jorgensen) дуговые полосы проектируют с уменьшающимися книзу радиусами, но приблизительно равными центральньши углами, причем наиболее экономичным центральным углом считают угол в 133°. Примером построенной по теории Ергенсена П. служит П., изображенная на фиг. 17 (план) и фиг. 18 (разрез); высота этой П. равна 60 м\ толщина дуговых полос от замка свода к пятам увеличивается на 50%. В новейших сводчатых П. расположены вертикальные водонепроницаемые швы, чтобы тем самым избежать моментов заделки. Экономичным пределом пролета сводчатых плотин признается пролет в ~200 м.

Как на типичные сводчатые П. можно указать также на П. Золя во Франции, перегораживающую ущелье шириною 7 л по дну и 67 jw на высоте 38 м, или на П. Пад-финдера (Pathfinder), сооруженную в ущельи шириной в 69 jh лишь на высоте 64 м от дна. В зависимости от ширины ущелья применяли радиусы в 30 м, 45 м, 122 м и пр. Сводчатые П. имеют часто незначительную толщину, чему примером может служит П. Сиксмайлкрик (Sixmilecreek) в Австралии; при высоте 10 м она имеет толщину всего лишь 2,40 м; радиус свода равен 20,5 м при ширине ущелья поверху в 30 м. Наибольшей по высоте сводчатой П. является в настоящее время П. Пакоима (Pacoima) высотою 114,3 м над ложем реки и на 121,92 м выше основания; пролет свода равен 164,59j№; радиус кривизны у гребня 97,54 м, у основания 35,05 м; ширина гребня 2,44 м; ширина у основания 29,26 м. Все, что сказано в отношении рациональной подготовки основания и береговых склонов для гравитационных П., относится не в меньшей степени, а по отношению к берегам ущелья еще в большей степени к сводчатым П.

4. Арочные П. Эти плотины состоят из ряда арок, опирающихся на береговые и промежуточные опоры. Ось таких плотин делается прямолинейной за исключением особых случаев, экономически оправдывающих несоблюдение этого правила. Арки делают к воздушной стороне сильно наклоненными, а их опоры получают треугольное сечение с расположением вершины в уровне наиболее высокого горизонта воды. Поверху устраивают помост для сообщения с берегами. С водной стороны устраивают защитную шпору, долженствующую служить основанием для арок и преследующую в то же время цель уплотнения самого основания. На фиг. 19 (план), 20 (вертикальный разрез) и 21 (горизонтальный разрез) изображена арочная плотина, построенная в Германии. Опоры всегда располагают на равных расстояниях друг от друга, чтобы они Ие подвергались боковым усилиям. При расчете

линию ее, изогнутую по дуге круга, причем толщину арки считают вдоль дуги одинаковой. Усилиями, действующими на такой jg арочный эле-

,/s,sff мент, являются: собственный вес, давление воды, усадка бетона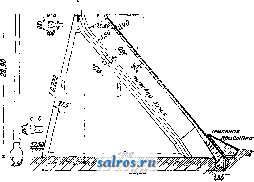

Фиг. 20.

и Г-ные изменения. Келен рассматривает давление воды: равномерное, происходящее на высоте замка арок, и неравномерное, вызываемое более пониженным расположением пят арки по отношению к ее замку. Г-ные изменения в после-строительный период д. б. во всяком слу-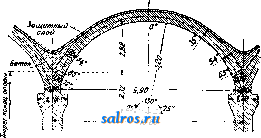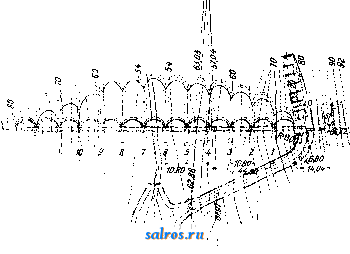

6А0 W.SO

Фиг. 19.

арки разрезают ее мысленно на отдельные элементы высотою 1 м каждый, причем плоскости разрезов д. ГТ2 б. пе]эпендикуляр-ны к производяше!! арки. Каждый арочный элемент считается жестко заделанным в сво-;ях пятах. За ось арки принимают среднюю \

I Уапо1еои.

Фиг. 21.

чае учтены. Температура замыкания каменных арок принимается в среднем равной 10°. Влияние усадки бетона приравнивают добавочному понижению температуры на 15°. Если не учитывают усадку, то в арках оставляют открытыми особые рабочие швы, к-рые бетонируют впоследствии после основной усадки. Кроме этих равномерных /,°-ных изменений необходимо учитывать также неравномерные °-ные изменения, происходящие от неравномерного нагрева водной и воздушной сторон арок. Необходимо предусмотреть прочную заделку арок в шпоры П., при железобетонных арках для этой цели увеличивают количество распределительного железа, прочно закрепляя его в шпоре. Усилия, вызывающие напряжения в арочном отрезке (фиг. 22) при угле наклона арки q>, выразятся следующим образом, а) Равномерное давление воды: горизонтальный распор.

Н , = -у„/1Ш'; (35)

изгибающий момент

М^Н^.у; (36)

нормальная сила

N =yoUvl + H.cosa. (37)

б) Неравномерное давление воды: изгибающий момент

+ (38)

нормальная сила

N, - \W и + Н'е^ COS <р] (39)

в) Равномерное изменение t°: гориаонталь-ный распор

Щ^ - ПП, (40)

изгибающий момент

Mt=Ht.yo\ (41)

нормальная сила

Jf = H,cos93; (42)

г) Неравномерное изменение t°: изгибающий момент

ЖдJ=*2( vl2д^. : (43)

д) Собственный вес: изгибающий момент

= [-Шг. t.+M;,+H;,(i - f)]yiгз;(44)

нормальная сила

= [im ? sin 9? -Ь Н'ед cos (p\y[V . (45) Напряжения у водной стороны: <г

ijv 6 2М

напряжения у воздушной стороны: а

6 2М

(46)

(47)

В ф-лах (35)-(47) буквенные обозначения имеют следующее значение (фиг. 22): I-

теоретич. полупролет, равный полупролету средней линии арки; h-глубина погружения внешней замковой точки рассматриваемого поперечного сечения арки; а- Фйг. 22. центральный угол, отнесенный к полупролету; наивыгоднейший размер а=75-90°; наивыгоднейшее очертание арки-полуокружность; Уо-УД- в. воды; -уд, в. арок; со- коэф. расширения бетона, равный 0,00001; В-модуль упругости бетона; q>-центральный угол, отсчитываемый от шелыги арки; t-изменение температуры по отношению к темп-ре замыкания арок; М-разность температур у внешней и внутренней поверхности арок. Вспомогательные величины: d- толщина арки; -угол наклона арки;

d. , I 1.

° i sin а 2

Уо = УоС08у; и=1-соз<р ~~<р81П(р; у\ = Ух COS V ; f 9> = 9? sin 9? + cos 9? - 1 >

V ч I л„ - 3 sin а .

Ki= bln2a-ba-acos2a-3-°;

* 8 4 а

К'з = 2 sin а - I sin 2 а - а -f ] а cos 2 а;

ii:,= sin2a-f а-2; 1Сб- 2Sin2a-ba;

2--cos а - 1;

£:,-acos2a-H4?-sin2a-a; - sin 2 а-~ а cos 2 а;

; Ег<; = 20т/Л12.1°;

2 Л sin а vaslnsa *

12 Za

. ТТ sin а \п

1; = --(ьу;

а 8in2 а

12 г

12 g Sin а

Sin a

, z( -cos.)-l(?i);

Уо- (-Ctga)l.

Приведенные вьппе ф-лы для определения напряжений в гравитационной П. примени-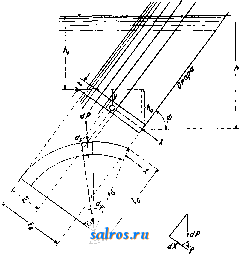

Фйг. 23.

МЫ также к расчету опор арочных П., если в этих ф-лах давление воды УоН заменить специфич. давлением, передаваемым арками на опору и слагающимся из соответствующего давления воды на арки и из компоненты их веса, перпендикулярной к обращенной к напорной воде грани опоры. Для определения давления воды, передаваемого наклонной аркой на опору, вырезываем перпендикулярными к образующей арки плоскостями кольцевой слой арки шириною t (фиг. 23). На элементарную площадку t-ds действует радиальное давление воды:

dP-t-dsih + yyyo, (48)

j/ = f cosv=r (l-cos97)cosv , (49) где Га-внешний радиус арки.

(50) *22

следовательно:

dP=t-rad(p [hi + Га (1 - cos <р) cos vl Уо (51) Вертикальная к опоре компонента равна: dX = dP cos (р = ynfrji cos (p dq> -\-+ Уоа COS V (cos 9? - COS 9?) dqj. (52) Интегрируя в пределах от О до а, получим: X = УоГа! Sin а + Уо?г2 cos у sin а - sin а cos а - I (53)

Величина X представляет собой давление на одну половину арки; на опору приходится следовательно давление:

2Х = 2уо/Гд/11 sin а + ytrl cos у [sin а (2 -- cos а) - а] = 2layothi + + yo cosy?2-b(cosa--j).

Величина 21аУо^К представляет собой давление воды на плоскую подпорную стенку П., перекрывающую пролет 21а (расстояние между двумя смежньпми опорами). Давление воды fe , выраженное в м вод. ст., произведет на опору при плоской подпорной стенке на глубине h то же действие, что и на арку, если 2Х разделить на 2а^Уо, т. е. если

2Х

= + ¥Ш-а^У'(---) (54) Если fa - стрелка арки, то

0 = fa cos 1р = Га{1 - COS О.) COS V =

(55)

а так как hi = h - ho, то

= ~ im ( ~ °) + -f cos (2 - cos а -

2 Sina V Sin a)

Ig COS V

(sia-tga)..T (56)

Выражение (56) относится ко всем элементам арки, расположенным ниже элемента, ключ которого совпадает своей низшей точкой с поверхностью воды; в этих пределах при определении давления на опоры давление воды h д. б. уменьшено на величину у^, зависящую от наклона опоры у водной сто-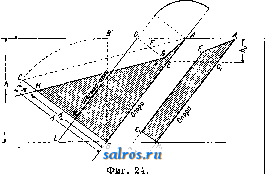

роны, от расстояния между опорами и от. формы арки. Выше точки D верхнего полностью омываемого элемента арки давление воды м. б. (достаточно точно) принято линейно понижающимся до нуля на уровне воды (фиг. 24). Вес арки, приходяпщйся на

долю опоры, легко определяют, когда определены размеры арки, после чего намечают размеры опоры, определяя вес ее и относящейся к ней нагрузки от мостового настила и временной нагрузки. Когда все силы, действующие на опору, выявлены, проверяют целесообразность принятых размеров опоры в отношении ее устойчивости, сопротивления скольжению и допускаемых напряжений, которые нигде не должны быть превзойдены. Келен рекомендует придавать опоре ширину поверху примерно в Vio Расстояния между опорами, уширяя опору книзу и придавая опорам жесткость посредством ригелей, располагаемых как с воздушной, так и с водной стороны. Наиболее выгодное расстояние между двумя смежньпии опорами зависит от высоты П., причем оно тем больше, чем выше П. По Ергенсену наивыгоднейшее расстояние между двумя смежными опорами варьирует в пределах 9- 15 м. При расчетах опор принимают наи-невыгоднейшее положение уровня воды, совмещая вершину треугольного сечения опоры с этим уровнем. Коэфициент устойчивости против опрокидывания принимается в пределах 1,5-2,0. Против скольжения опоры последняя сопрягается с основанием зубцами, выделанными в основании; коэф. трения =0,8. Если скала имеет падение в сторону нижнего бьефа, то основанию придают или горизонтальную или наклонную с подъемом в сторону нижнего бьефа поверхность с вьщелкой, как вьппе указано, зубцов в основании П. Арочные П. требуют меньше строительного материала, чем массивные (гравитационные) П., но они требуют добавочного расхода на подмости и опалубку, высокого качества материалов, опытных квалифицированных рабочих и более тщательного выполнения работ; все это влечет за собой удорожание П., вследствие чего арочные П. обходятся б. ч. не дешевле гравитационных.

5. Амбурсенские П. В то время как у арочных П. напорная грань представляет собой ряд арок, П. по типу Амбурсена имеют плоскую напорную грань. Особенно большое количество последнего типа П. построено компанией Амбурсен в Америке. Плоские напорные жел.-бет. плиты наклонены к воздушной стороне и поддерживаются опорами, схожими с опорами арочных П.При расчете напорную наклонную стенку П. разбивают на отдельные плиты, свободно лежащие своими концами на опорах, вследствие чего устраняются боковые усилия на опоры, а растягивающие усилия в плитах возможны лишь у воздушной стороны; благодаря этому появление с этой стороны трещин не влечет за собой повреждения арматуры. Если выделить из общей поверхности плиты полосу шириной в 1 л*, то согласно обозначениям на фиг.25эта полосабудет подвержена моменту: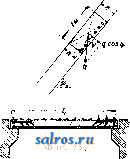

- gl?(y/i+riWcosv), (57)

где h-глубина воды над серединой плиты в ж; 7J-уд. в, железобетона; w=w+e; е- расстояние ц. т. арматуры от крайнего растягиваемого волокна; 1-расчетный пролет. Подставляя в ф-лу (57) значение величины п и пренебрегая величиной cosv получим:

М=\ц (yh + уХ cos у}). (58)

Рабочая высота

w = а ум, (59)

а площадь сечения арматуры:

feVM, (60)

где коэф-ты а и при допускаемом напряжении железа а=1 ООО кг[см и при допускаемом напряжении бетона (т^, имеют следующие соответственные значения:

Ъ в кг/сл(г . . 20 25

........ 0,217 0,180

(<........ 5,00 6,13

30 0,155 7,21

35 40

0,137 0,123 8,25 9,26

....... 0,231 0,273 0,310 0,344 0,375

Арматура изгибается, и бугеля распределяются так же, как у свободно лежащей балки. Опорное сопротивление принимают распределенным по опорной поверхности по тр-ку (фиг. 26). Расстояние [Г[11 I ! между опорами берется обыкновенно в пределах 4-6ж; опоры получаются при этом расстоянии тонкими и требуют поэтому в местах при, S ! мыкания к ним плит ушире-

N/f i i НИИ в виде консолей. Опорное давление плитной полосы в 1 Л1 ширины выражается величиной:

Л= (yh+yn cos v)-(61)

то с =

а и консоль

Фиг. 26.

Если взять а = , -

будет подвержена изгибающему моменту

М = Ас li {yh+yn cos у}) (62)

Зная полезную высоту консоли до середины арматуры, равную b = aVM, определяют величину а, затем по приведенной выше таб-липе величины o-ft. /3 и нулевое расстояние х и по ф-ле (60) величину Д. Плечо внутренних сил равно:

а трансверсальное напряжение будет

А--- ice Ь -

(63)

(64)

Плиты- изготовляют толщиной <{:0,30 л1 и скрепляют со шпорой. Опоры сооружают из бетбна или железобетона и взаимно крепят балками; метод расчета опор амбурсенских П. тот же, что у арочных П. При большой высоте П. применяют взамен гладких ребристые плиты. На фиг. 27 и 28 представлена

плотина Комбамала, построенная по типу амбурсенских плотин и имеющая высоту 40 м. Собственный вес этих П. сравнительно

незначителен, вследствие чего для устойчивости плотины и обеспечения ее от скольжения придают напорной грани значительный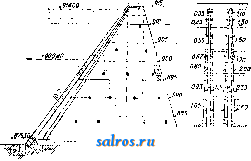

i4s-ZZm --------4.0--10.80- х<

Фиг. 28.

уклон. По Франциусу наиболее целесооб-разньш углом наклона плиты является по-видимому 45 . Расчет производят по нормам,

По 8-В

2£5 Фиг. 29.

По а-а

Фиг. 30.

принятым для железобтьотшх %ожтрук-ций (см.), обращая особое внимание на скалывающие напряжения; погерманск. нормам скалываюпще напряжения д. б. целиком восприняты рабочей арматурой; в Америке считают возможным передать половину скалывающих напряжений на бетон.

6. Другие типы каменных П. В Америке применен впервые в 1903 г. тип куполообразной П. высотою в 9 л*. Плотина Кулиджа построена в виде трех сферических сегментов, расположенных по дуге круга. Оригинальным типом является сотообразная плотина (фиг. 29), предложенная Гуцвиллером. В П. системы Фига-ри тело П. (фиг. 30) имеет внутренние вертикальные колодцы, преследующие (так же как в сотообразньЕк плотинах Гуцвиллера) цель

удаления внутреннего слабо работающего ядра массивной П. Однако экономия в материале поглощается в этом случае расходами, связанными с применением сложных подмостей и опалубки (в целях обеспечения надлежащей водонепроницаемости). На фиг. 31 представлен разрез П, системы Фигари (плотина Rochemolles в Италии), Дабы избежать устройства дорогих подмостей и опалубки и в то же время съэкономить материал. Келен предложил свой тип П изображенный на фиг, 32 и представляющий собой переходный тип от гравитационной П, к арочной. Подобный же пе-реходньай тип предложил Ноэтцли; слабым местом системы (фиг. 33) является уплотнение в соединительных щвах; головные части опор очерчены по дуге круга т. о чтобы избежать изгибающих напряжений. К новаторству в постройке каменныхП, следует отнести также раздельные П., состоящие из ряда тон- По c-d ких стенок, расположенных друг за

Фиг, 31,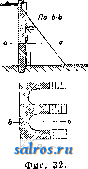

По а-А

Фиг, 33,

другом в виде уступов. В данном случае массивная плотина как бы разбивается вер-тикальньили плоскостями на части, раздвинутые на равные расстояния друг от друга (фиг. 34). Напор, действуюпщй на каждую стенку, соответствует разности двух смежных горизонтов. По старому проекту промежутки между стенками предполагалось засыпать землей, по новому проекту Гутенберга (фиг. 35 и 36) они заполняются водой. Хотя давление воды на каждую выше расположенную промежуточную стенку в пределах от гребня соседней ниже расположенной стенки до основания является одинаковым, однако изгибаюпще напряжения возрастают книзу, вследствие увеличения плеча момента. По проекту Ме-нажа стенки имеют в плане криволинейное

Фиг. 34.

очертание и работают как своды; плечо момента в этом случае не играет никакой роли, благодаря чему стенки могут иметь весьма незначительную толщину. Однако конструкция таких стенок отличается большой сложностью, в особенности если плотина составляется из нескольких систем сводов. В отдельных промежутках напорные стенки д. б, соединены между собой поперечными стенками (фиг. 35 и 36) и притом так, чтобы при колебаниях уровня воды не получались опасные напряжения; это как-раз является слабым местом этой конструкции, не говоря уже о высокой стоимости опалубки.

Все эти и другие типы П. представляют собой попытки разрешить вопрос о наиболее рациональной конструкции П. Однако за последнее время уже твердо установился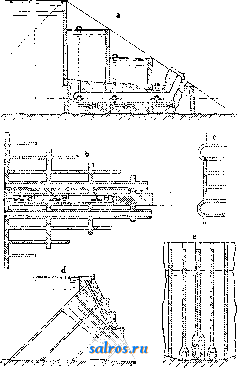

Фиг. 35.

тип П. с треугольньгм профилем, с заложением верховой грани 0,05, иногда 0,03 и низовой 0,65-0,85, причем последний размер определяется гл. обр. в зависимости от принятого предположения о давлении фильтрационной воды. Придание П. гравитационного типа кривизны в плане не считается обязательным и вопрос этот решается в каждом отдельном случае в зависимости от местных условий и материала, из к-рого сооружается П. Ширине поверху массивных П. придают обычно размер ~ 5 дг, увеличивая эту норму в случае опасения большого давления льда или ударов плавающих тел. Вместо сплошного уширения иногда прибегают в целях экономии кладки к уширению в виде отдельных контрфорсов, соединяемых арками, примером чему может служить Днепровская П.