• Что такое фактурная штукатурка
• Выбираем сухие строительные смеси
• Преимущества напряженного железобетона
• Что влияет на выбор кровельного материала
• В чем преимущество пробковых полов

Фиг. 4.

закрывается, когда ось объектива направляется вниз. Прежде этот затвор состоял из стеклянной кюветы с параллельными стенками, сообщающейся с сосудсм, наполненным ртутью. При наклоне кюветы она наполнялась ртутью и закрывала проход лу-ча.м. Однако с течением врем*ни на стенках кговеты образовывался осадок, уменьщав-щий прозрачность. В последних моделях затвор дрлается механическим, основанным на принципе карданова подвеса.

Из подвижных светил планетарий сист. Цейсса воспроизводит Солнце, Луну, Меркурий, Венеру, Марс, Юпитер и Сатурн, т. е. все планеты, видимые невооруженным глазом. В решетчатой ферме 11 размещены в трех этажах Сатурн, солнце и луна. По другую сто{юну в ферме 75 расположены механизмы остальных четырех планет. Движения планет воспроизводятся механизма.ми, которые представляют модель Копер-никанской системы. Для примера рассмотрим механизм Марса (см. фИ1. 4). На месте планеты находится шарнир М, который обращается с постоянной угловой скоростью около центра С; с шарниром скреплен стержень МА, проходящий через My(J3Ty Е, представляющую Землю и со-веритающую тоже круговое движение с соответствующей угловой скоростью. На конце стержня находится проекционный фонарик р, бросающий изображение планеты на экран. Ясно, что если М совершает гелиоцентрическое движение Марса и Е-такое же движение :}емли, то луч света на экране воспроизводит геоцентрич. движение Марса. На самом деле ради удобства конструкции стержень заменен сочлененным п а ра л л ело г ра мом, но это не меняет принципа механизма. В приборе учтены наклоны плоскостей и эксцентриситеты орбит. Первое достигается весьма просто соответствующим на-клоно.м плоскостей враи1ения точек М и Е(верхняя фиг. 4). Эксцентриситеты приняты во внимание тем, что движепие планеты со-вер1иантся равномерно относительно некоторой точки С, причем последняя не находится в центре той окружности, по к-рой движется планета, но отстоит от него на расстоянии удвоенного линейного эксцентриситета орбиты Т.о. удается представить ур-ие центра в эллиптич. движении с точностью членов первого поря,т,ка относительного эксцентриситета. Для Меркурия в виду больнюго эксцентриситета его орбиты механизм слож-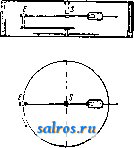

Фиг. 5.

Фиг. 6.

нее, так как нужно было не только соблюсти правильное гелиоцентрические угловое движение планеты, но и воспроизвести изменение длины его радиуса-вектора. Проще всего механизм для солнца. В этом случав направление проекционного фонаря задается землей В, движущейся вокруг неподвижной точки iS - солнца, на фиг. 5 ради простоты показанной в центре земной орбиты. На самом деле и здесь учтен эксцентриситет. Наибольшей сложностью отличается м еханизм для л у ны, для которой пришлось воспроизвести не только наклон плоскости орбиты, но и движение лунных узлов. Последнее достигнуто в[)ащениемвсей орбиты 2-2 (фиг. 6) посредством гильзы в плоскости 3-3 с периодом в 18,6 лет. Конечно неподвижной точкой при движении луны М является уже не солнце, а зе.мля Е. В фокусе фонаря, проектирующего луну, помещается круглое вогнутое зеркальце, перед к-рым вращается особая диа([)рагма, закрывающая зеркало и тем воспроизводящая фазы луны. Т. к. механизмы планет находятся внутри решетчатых ферм, переплеты к-рых могут отчасти затемнять изображение, все фонари планет двойные и выверены так, чтобы их изображения совпадали. Ког.а затмевается один фонарь, другой продолжает давать изображение в нужном месте экрана.

Представляет интерес расчет передач. Для этой цели отношение времени обращения данной планеты и земли разлагают в непрерывную дробь и затем находят ряд подходящих дробей. Одна из последних, достаточно высокого порядка, еще исправляется небольшой поправкой, подобранной так, чтобы числитель и знаменатель разлагались на небольшие множители. Так напр.. период обращения Марса, равный 1,8808152 г., представляется с большой точностью дробью

p-f= 1,8808163. Эти множители и дают

число зубцов в соответствующих передачах. Движение планет удалось воспроизвести с такой точностью, что ошибка из-за неточности передач не превосходит 1° на 5 ООО оборотов земли, т. е. лет. Электродвигатели 19 (фиг. 2), управляющие движение.м планет, имеют различные скорости, а именно 1 г. в 4 мин., 1 мин. и 7 ск. Если ни один из этих двигателей не включен, то планеты увлекаются суточным вращением, и воспроизводится точная картина всех видимых движений. При остановке суточного вращения и пуске планетных двигателей движения планет демонстрируются на фоне неподвижного неба, причем типичные черты этих движений м. б. прослежены в короткое время. В аппарате имеется еще возможность вращения всей проектирунщей системы около оси Э1СЛИПТИКИ 2-2 (фиг. 2), что вызывает явление прецессии (см.), совершающееся

в природе с периодом ок. 26 ООО лет (фиг. 7). И наконец ряд добавочных, частью неподвижных, частью подвижных фонарей про-

Ы.15000г.

Соянцг

Фиг. 7.

ектируют Млечный путь, некоторые туманности, названия созвездий, сетку экваториальных координат, меридиан и эклиптику. Имеется еще счетчик, указывающий номер года, соответствующего данному положению планет.

Общее число всех проекционных фонарей в последней модели равно 119. Все управление аппаратом сосредоточено в лекторском пульте с распределительной доской, соединенной 40 проводами с инструментом и позволяющей включать различные проекционные фонари и давать те или иные движения в зависимости от демонстрируемого явления. В руках лектора имеется небольшой фонарь, проектирующий яркую стрелку, служащую для указания на тот или иной объект на экране. Экран состоит из белого полотна, натянутого на деревянные рейки, расположеннью параллельными кругами и в свою очередь прикрепленные к железному решетчатому каркасу. Каркас собирается из почти 8 ООО железных палочек ок. 60 см длиною, которые образуют пяти-и шестиугольники, скрепляясь в вершинах этих многоугольников по 5-6 штук одним общим болтом. Диаметр полотняного купола в разных П. различен. Наименьший диам., в 12 jh, имеет П. в Мюнхене, наибольший, 30 м,-в Дюссельдорфе. Чаще всего берется диам. в 25 л . Вместимость зрительного зала при таких размерах составляет ок. 600 чел., хотя боковые места около периферии зала вследствие перспективного искажения неудобны для зрителей. Внутренний купол окружен внешним куполом, часто делающимся железобетонным. Простейшая форма последнего тоже полусферическая; однако в этом случае получается очень плохая акустика вследствие возникновения эхо, для уничтожения которого между полотняным и наружным куполами размещают в возможно большем беспорядке неправильно отражающие звук железные листы. Общее число всех П. системы Цейсса к 1931 г. составляло 18. Один из них, построенный в 1929 г.,

находится в Москве. а. Михайлов.

Московский п. системы Цейсса, открытый в ноябре 1929 г., установлен в специально -построенном двз'х:этажном железобетонном здании с огромным, параболич. формы, железобетонным куполом. Общая высота всего здания равна 32 м. Здание (фиг. 8) представляет собою оригинальное архитектур-

ное произведение в духе повой современной архитектуры (проект архитекторов Бар-ща и Синявского). Диам. наружного параболич. купола 30 м. Диам. внутреннего купола (экрана) 25 м. Работы по постройке вел Мосстрой, произведя ее в 13 мес. В нижнем этаже расположены: вестибюль, фойе на 500 чел., главная лестница, малая аудитория на 120 человек, две круглых выходных лестницы, гардероб, кассы, две комнаты бухгалтерии и месткома, две комнаты дирекции, уборные и трансформаторная будка МОГЭС. Кроме того в фойе имеется широкая лестница, ведущая в полуподвальный этаж, где расположены постоянная антирелигиозная выставка-музей, библиотека, читальня, лабораторная комната, фотолаборатория, комната отдыха сотрудников, буфет. В верхнем этаже помещается главный круглый зрительный зал на 500 мест в 26 м диам., с полотняным в виде полусферы белым куполом-экраном. Низ купола окаймлен силуэтами московских зданий, видимых с крыши П. Из зала можно попасть в межкупольное про-

Фиг. 8.

странство, где идут трубы отопления и приточной вентиляции. К зрительному залу примыкают комната для хранения аппарата Цейсса, куда последний выкатывается по специальным рельсам; комната лекторов; вьгходные двери (две); выход на балкон и в кинобудки. Кинобудок имеется две: одна для обслуживания главного зала, другая- для малой аудитории. Котельная и вентиляционная камеры, а также умформерная комната, расположенная в пристройке правого крыла фасада. Вокруг наружного купола идет круглый балкон, предназначенный для переносных астрономич. инструментов по наблюдению неба. Кроме того для этой же цели используются плоские крыши пристроек: аппаратной комнаты и кинобудки. Стоимость здания ок. 600 ООО р.

Оборудование московского П.-гл. обр. заграничное, высокого качества. Главный проекционный аппарат Цейсса, стоимостью 150 ООО р. золотом, постоянно пополняется рядом нововведений - усовершенствований со стороны фирмы Цейсе, к-рая присылает те или иные дополнения и изменения соответствующих частей аппарата. Кроме этого сами работники московского П. вводят ряд существенных изменений и усовершенствований аппарата Цейсса; так напр., изобретен

аппарат для рассвета и восхода яркого солнца, аппарат для демонстрирования частных, кольцеобразных и полных солнечных затмений и др. Московский П. является единственным в нашем Союзе; имеет пропускную способность около 1 000 000 чел. в год. Уже пропушено ок. 1 300 ООО посетителей, что говорит об огромном интересе трудящихся к этому культ^фпо-просветнтельному учреждению. Московский планетарий, не в пример заграничным, служит единственным в мире планетарием, раскрепощающим трудящихся от гнета религиозного дурмана и помогающим им, на основе данных современной науки, в выработке правильного, марксистско - ленинского диалектического миропонимания.

Jlvm.: Преображенскп!! Н. и Поляков А., Что такое планетарий, М., 19.30; Баев К., Ш и от о в оки й Б., Якобсон А., Планетарий, Москва, 1931; П[истовский К., Московский ананетарий Цейсса, Русский астрономический календарь на 1930 г. , Нижний-Новгород, 1930; Г. П. 391036; V 1 1 1 1 g е г W., О.ч.ч Zeissche Projektions-planetarium, Jena, 1925; Villlger W., Zeiss-Planetarium, Jena, s. a.; A u e г b a с h F., Planeta-rien, Leipzig, 1928; Villlger W., Vom Aufban d. Zeiss-Planetariurn, Jena, 1928; Meyer F., Z. d. VDJ , 1925, 46; Bauersfeld W., ibid.. 1924, 31; В a u-er.sfeld W., Da.4 Zeissclie Projektionsplanetariuin, Jena, 1925; M orison G. H., Scient.ific A.merican , New York, 1925. K. Шистовский.

ПЛАНИМЕТР, инструмент для механич. определения площадей фигур на бумаге в мелких квадратных единицах (см, мм) или в земельных мерах (га, м^). П. подразделяются на две группы: полярныеП., которые при употреблении вращаются около одной неподвижной точки (полюс), и лине й н ы е, перемещаемые по плану параллельно своему первоначальному положению.

А. Наиболее распространены в геодезич. практике полярныеП.; лучший из них компенсационный П. механика Коради: он является усовершенствованным видоиз.менением П. Алюлера. П. Коради существуют двух видов: 1) с постоянным рычагом и 2) с переменным; они различаются между собой устройством свободного рычага и расположением счетного механизма относительно точки пересечения рычагов.

П. с и о стоя н н ым р ы ч а г о м (фиг. 1) состоит из двух отдельных рьгаагов, к-рые

Фиг. 1.

для работы составляются вместе. Один из них называется полюсным, другой- обводным. Полюсный рычаг-металич. брусок, к одному концу которого приделан медный цилиндр Р. Снизу цилиндра, в его центре, вделана тонкая игла (полюсП.), к-рая во время работы вдаливается в бумагу и остается неподвижной. Для уменьшения тгрения низ цилиндра Р сточен т. о., что в средине получается небольшой выступ, перпендикулярный к направлению рычага. На другом конце бруска прикреплен конич. формы стальной отросток G, оканчивающийся шариком. При соединении рычагов этот

отросток вкладывается в гнездо обводного-рычага полушарообразной формы. Обводный рычаг состоит из двух частей. Одна-часть-небольшой брусок такого же вида, как и у полюсного рычага. В свободном конце его вставлен обводный шпиль (игла) с небольшой пружиной и грифом F. Этот гриф* держат пальцами при обведении фигуры. Снизу грифа ввинчивается подставка, устанавливаемая так, что обводный шпиль только слегка касается бумаги и не царапает ее. Сбоку этого бруска нарезана полумиллиметровая шкала для установления обводного рычага на определенную длину. Другая часть обводного рычага представляет собой-металлич. отлив с тремя выступами. В удлиненном его конце сделан желобок, в к-рый: вставляется брусок, с обводным шпилем и закрепляется винтом, проходящим снизу. Между выступами Т, Т помещается счетный^ механизм, состоящий из циферблата, счетного колеса и верньера (см.). Счетное колесо-(валик) наглухо скреплено с осью, в средине к-рой сделан бесконечный винт. Концы оси конич. формы входят в углубления небольших подшипников, С помощью винтов S, S можно изменять положение этих подшипников и сообщать оси продольное перемещение. Счетное колесо цилиндрич. формы, с металлич. ободком, сделано из белого целлюл оида. Поверхность колеса разделена на. 100 равных частей и занумерована через каждый десяток деления цифрами О-9. Для оценки десятых долей деления колеса рядом с ним установлен верньер. У первого штриха верньера подписана цифра О и у последнего 10. К бесконечному винту оси счетного колеса прилегает шестерня, скрепленная с осью вращения кружка (циферблата). Поверхность кружка разделена на 10 равных частей, отмеченных цифрами О-9. Сверху кружка через его центр проходит отросток, оканчивающийся острием, которое служит-указателем (индексом). Бесконечный винт и шестерня сделаны с таким расчетом, что одному полному обороту счетного колеса соответствует 0,1 полного оборота циферблата. Счетный механизм дает возможность считать полные обороты счетного колеса (по-циферблату), десятые и сотые доли его оборота (на самом валике) и тысячные доли ето оборота (по верньеру). На свободном выступе свободного рычага помещается опорное колесо С, вследствие чего вся тяжесть П. распреде.т1яется на 4 точки опоры: полюс, свободный шпиль, ободок счетного колеса и опорное колесо.

П. с перемени ым ры ч а гом (фиг. 2> отличается от описанного устройством обводного рычага. Этот последний состоит из длинного бруска FL (-23 см) с изогнутым

Фиг. 2.

концом, в к-рый вставлен обводный шпиль-F. Для соединения со счетным механизмом рычаг вставляется в 2 муфты, находящиесяч на противоположной стороне выступов Т,

и закрепляется двпля нажимными винтами К (второй винт находится на выступе с опорным колесом С и на фигуре не виден). Для сообщения рычагу медленного движентгя, он вкладывается в третью муфту М с нажимным кинтом К^. При ПО.МОЩИ микрометрического винта, обвитого пружинкой, муфта М соединяется с выступом Т. Чтобы устанавливать рычаг на определенную длину, .на верхней его грани нарезана полумиллиметровая шкала, а сверху рамы счетного механизма прикреплен верньер V. Для такой установки ослабляют нажимные винты К, KiVi движением руки устанавливают рычаг сначала грубо на требуемую длину; затем, закрепив винт Ki, действуют гайкой при муфте М, устанавливают рычаг точно по верньеру и закрепляют нажимные винты Я . В других деталях П. с неременным рычагом подобен вышеописанному П. с постоянным рычагом.

При соединении рычагов свободный ры-чаг будет вращаться около воображаемой оси, проходящей через центр шарика, к-рый находится на конце отростка G, и перпендикулярной к плоскости чертежа. Эту линию называют осью вращения П. Расстояние от оси до полюса примем за длину полюсного рычага, а расстояние от оси до обводного шпиля-за длину обводного рычага. Чтобы практически получить длину обводного рычага, устанавливают на бумаге этот рычаг и делают 2 накола-обводным шпилем и иглой-через отверстие, просверленное в шарообразном гнезде рычага. Последний накол будет проекцией оси вращения. Расстояние между наколами принимают за длину обводного рычага. Для получения длины полюсного рычага удерживают в ТОМ же неподвижном положении обводный рычаг, осторожно вкладьшают в гнездо отросток G, нажимают цилиндр Р и получают полюс П. Расстояние между полюсом и проекцией оси вращения есть длина полюсного рычага.

Теория П. разрабатывается при условии, что плоскость ободка счетного колеса перпендикулярна к направлению обводного рычага. I) Положим, обводный рычаг перемещается параллельно самому себе

--.-

т

Фиг. 4.

Фиг. 3.

ж из положения / перейдет в положение (фиг. 3). Ори этом ободок C4eTHorvj колеса К обернется на такую дугу и своей окружнисти, к-рая равна перпендикуляр-саому расстоянию h между I и II положениями:

u = h. (1)

2) Если обводный рычаг перемещается параллельно самому себе, но под углом к направлению счетного кол1са, например по линии KKi (см. фиг. 4), т~> колесо одновременно и вращается и скользит. Такое движение разлагается на два: по направл1нию KKi и по направлению AlKg. Вследствие вращения колесо обернется на дугу h,A от скольжения он) не сделает ни одного оборота. Следовательно и в этом случае

U = /I. (2)

J) Если обводный рычаг вращается около нек-рой точке а н на Положения аЪ перейдет в положение ас

(Фиг. 5), то счетное колесо К переместится в К^, обернувшись на дугу ы. Длина дуги и будет зависеть от расстояния колеса К до точки а. Обозначив это расстояние через (?, дугу при радиусе, равном единице. Соответствующую углу Ьас, через fi, имеем:

U=&Q. (3)

4) в общем случае, когда обводный рычаг из какого-либо Положения перемещается в другое произвольное, а , Н ь

Фаг. 6.

напр. из положения аЬ в положение cd (фиг. 6), такое движение можно разложить на два: сначала считать, что рычаг из положения аЬ передвинулся параллельно самому себе и занял положение сс, а затем, повернувшись около точки с, перешел в положение cd. На основании предыдущего дуг.1, на которую обернулось Колесо К при переходе из К в К^, выразится:

wh+Pg, (4)

Для П. с переменным рычагом ф-ла (4) обратится в u = h-Pii (5)

вследствие того, что счетный механизм в таком П. находится за точкой пересечения рычагов, и при вращении обводного рычага около точки с на дугу /J (для перехода из сс в cd) счетное колесо будет вращаться в обратную сторону против вращения, когда оно переходило из аЪ в cci (фиг. 7). При движении обводного шпиля по контуру фигуры счетное колесо будет и вращаться и ско.11ьзитЬ. т. о. путь, пройденный колесом на бумаге, вообще будет более (иногда равен) дуги, на к-рую счетное колесо обернется при своем перемещении.

Положим, требуется вычислить площадь фиг. 8. Установим П. так, чтобы его полюс Р находшюя внутри фигуры. Обводный шпиль поставим в точку а контура

фигуры. П. займет положение аЬР, причем аЬ =R есть свободный рычаг и 6Р = Rj-полюсный. Передвинем обводный шпиль на очень малую часть контура асхйх и поставим его в точку Oj. П. займет положение OijjP и пройдет элемент площади (jbPb,aiCia. При этом точка Ь П'ресечения рычагов п рнмес-тится в bj, и полюсный рычаг И\ пройдет площадь сектора hbP Движение обводного рычага Н из об в а|Ь] разложится на два: 1) обводный рычаг R из положения аЬ ц<;редвииулся в положение cbi параллельно самому себе и 2) повернувшись около неподвижной точки 6i, он из положения cbi перешел в положение Oibi. При движении из аЬ в cbi обводный шпиль опишет дугу ас, параллельную дуге bbi, и будет отклоняться от контура на величипу cci. Т. к. длина контураacjai по предположению весьма мала, то уклонением ccj можно пренебречь и считать, что точки с и cj совпадают. На основании того же предположения дуги at и bbi можно принять за прямые и площадь abbiCi считать па((Яллелограмом. Если бы элементарная площадка abPb\aiCia была бесконечно мала, то такие допущения были бы совершенно точны. Т. обр. элементарная площадь разделилась на три площади: па раллелограм abbjC и два сектора ЬРЬ^ а cbjai. Обозначим элементарную площадь abPbiOiCja через р; дугу при радиусе, равном единице, соответствующую углу ацау, Ч1!рез §\ дугу при таком же радиусе, соответствующую углу bPbi, через ?> Удерживая прежние обозначения, будем иметь: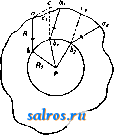

Фиг. 8.

Rh + \ caiR+\bbiRi.

В этом выражении, на основании (4) h =и + Pq. На основан'ш пропорциональности дуг своим радиусам cai=PR и bbi = <fRi Подставив эти выражения вместо равных им в ур-ие (6), будем иметь:

p=Ru-RPQ+\pRi + \vRb (7)

Передвинем обводный пшиль также на весьма малую часть контура Oiaj. П. займет положение а^ЬгР, прой-

дя новый элемент площади aiazbPbiai. Этот элемент подобно предыдущему можно разложить на 3 площади и выразить ф-лой, подобной ф-ле (7,. Т. к. часть контура OiOg вообще не равна части aai, го новый элемент площади не равен П|)ед),гдущему, и в выражении этой площади величины и, и ф будут иные. Обозначив через Pi элементарную площадь aiaabgPbiOi, буде.\1 иметь:

Для следующего элемента площади получим Ps = fiuj - RiQ + а 4-1 у^д

и'т. д. По обведении обводным шпилем всего контура П. пройдет ряд элементарных площадок и займет первоначальное положение адР. Чтобы получить выражение всей плогцпди фигуры, надо взять сумму выражений всех эл1ментариых площадей. Складывая почленно предыдущие выражения, будем иметь:

P + Pl + P2 + ... = H(W + Wl + U2 + ...)-

-RQ(P+Pi + Pi + ...) + R(+Pi + P3 + ..-)+

+ ~Rbv + Vi + 4>i + ...).

В этом выражении p+Pi + Pi +... дает общую площадь Р фигуры. Сумма U + UI + ... представляет сумму дуг, на к-рую обернулось счетное колесо при обведении всего контура и к-)ую обозначим через U. Суммы Ф+Р1+Рг + --- и <р+ч>1+ч> + выражают суммы дуг при радиусе, равном единице, и каждая в oтдЛьнooти равна 2п. Что сумма v+4>i-\-... равна ?л, видно из чертежа, т. к. точка иеррс<чения рычагов Ь при полном обведении конту[га опишет полную окружность. Для ,10казатеЛ1.ства того, что сумма ?¥Рх+... рав la 2я, возьмем ироизво.)Ы1ую точку и из нее проведем линии, параллельные всевозможным положениям обводного рычага. При точке построятся углы, соответствующие величинам 0, Рз, .... При цолно.м обведении контура сумма пост1..оенных углов будет равна 361)°, и сумма дуг, им соответствующих, при радиусе, равном единице, будет равна 2я. Ыа этом основании ф-ла (8) представигся так:

Р = й С/ - 2я В е + яй 2 + яЛ 1,

или

Р = Ди-Ьл(К2 + д? 2Ке)- (9)

Для П. с переменным рычагом последний член в ско.б-ках на основании ф-лы (5) будет иметь положительные знак, и ф-ла (9) представится в таком виде:

Р== RU + 7i(Ri + Rf± 2Rq). (10)

Формула(10) является общей для обоих видов М. Второй член формулы (10), зависящий от размеров П., есть величина постоянная. Обозначив его через Q, будем иметь:

p=m + Q. (11)

Для исключения постоянного Q из формулы (И) поставим полюс П. вне контура фигуры в точку с (фиг. 9) и обводный шпиль в точку а контура. При обведении контура по ходу часовой стрелки обводный шпиль будет проходить через точки й, tti, ttg, лежащие на верхней части контура. П. будет занимать при этом положения аЪс, abiC и т. д. Обводный шпиль, дойдя до нек-рой предельной точки, напр. 3, будет дврггаться по нижней части контура, и П. будет перемещаться в обратном направлр-нии. При движении обводного шпиля по верхней части контура пространство между начальным и последующими положениями рычагов будет увеличиваться, т. е. бу-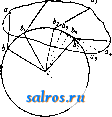

Фиг. 9.

дут увеличиваться до некоторого предела суммы: Р + 1 + 2 + .... 9> + Pi + <Pt +- . При движении шпиля по нижней части контура это пространство будет уменьшаться, и когда П. займет первоначальное положе-mie abc, суммы + Pi д> + g>i + ... об-

ратятся в нуль. Вследствие этого в формуле (8) три последних члена, содержащие /8 и (р, обратятся в нуль, следовательно обратится в нуль постоянное число Q=n(R + + В1±2ЯдУ, ф-ла (И) примет вид

Р^- ни. (12)

Итак, для вычисления площади фигуры имеем две формулы: при установке полюса внутри фигуры-ф-лу (И) и при установке полюса вне ее контура-ф-лу (12). При измерении площадей выгоднее полюс П. ставить вне контура фигуры. Кроме того при вычислении площадей старыми П., у которьгх концы оси счетного колеса достаточно износились, замечается продольное шатание оси. В таком случае расстояние между точкой пересечения рычагов и счетным колесом постоянно изменяется, т. е. о является величиной переменной и само постоянное числе Q-не надежным.

Практическое пользование П. Соединив рычаги, выбирают место для постановки полюса по возможности вне контура фигуры. После установки полюс.i, делают пробное обведение фигуры по ходу часовой стрелки. Если окажется, что при обведении рычаги составляют между собой слиатом острые или тупые углы, то положение полюса меняют. Выбрав окончательно место для полюса, устанавливают обводный ншиль в одну из точек контура, к-рую считают начальной, и делают отсчет.

Допустим, что циферблат и счетное колесо расположились так, как показано на фиг. I и. Отсчет делаю так:сначала смотрят на

Фиг. 10.

циферблат и с него берут цнфру, меньшую из тех, между к-рыми находится индекс (в данном случае 6). Затем смотрят на счетное колесо и записывают меньшую цифру из тех, между которыми находится нулевой штрих верньера. На фиг. 10 это цифра 5 (десятые доли оборота колеса). Отатой цифры считают по черточкам сотые доли-их

будет 4. После того по верньеру оценивают тысячные доли оборота, н-рых будет 6 (т. к. совпадает 6-я черта). Полный отсчет будет: 6 546 (тысячных). Сделав отсчет, осторожно обводят шпиль по контуру фигуры, двигая его по ходу часовой стрелки. Доведя обводный шпиль до начальной точки, снова делают отсчет указанным способом. Пусть этот отсчет будет 7 907. Разность отсчетов, равная 1 361, укажет, что ободок счетного колеса при обведении контура обернулся на l;}, *! тысячную своей ок( ужности. Для по-пучения плошади в натуральных (мелких) или земельных мерах эту разность надо умножить на некоторый коэфициент.

Обозначив отсчет до обведения контура фигуры через w, отсчет после обведения- через Wg и коэф. через fe, искомую площадь Р выразим след. обр.:

Р=к (Шг - mi).

(13)

Геометрическое значение постоянного числа Q. Поставим рычаги планиметра под таким углом, чтобы виобр;жаемая плоскость ре (фиг 11), п[10ходящая через ободок счетного колеса, прошла через полюс. Составится остроугольный тр-к, в котором обводный рычаг [{ мо>кет служить основанием и ра-его высотой. При таком положении ры-

030120

чагов расстояние между полюсом р и обводным шпилем о, равное D, будет величиной постоянной. Применяя теорему геометрии о квадрате стороны, лежащей против острого угла, будем иметь:

Для П. с переменным рычагом, у которого счетный механизм располояен за точкой пересечения рычагов и угол b тупой, последний член 2Ле будет иметь положительный знак. Предыдущая ф-ла будет общая для обоих видов П. и представится так:

Di = Rs+Rl±2RQ.

Это есть тот трехчлен, к-рый в выражении постоянного числа Q заключается в скобках (формула 10). Заменяя его через D2 будем иметь:

Q = я(R-ЛJ±2i?e) = яD, (14)

Следовательно постоянное число геометрически представляет площадь круга с радиусом D. Если начертить круг с радиусом D, поставить в центр круга полюс П. и обводным шпилем обвести окружность круга, то при обведении счетное колесо не сделает ни одного оборота. Это произойдет благодаря тому, что плоскость счетного колеса будет всегда перпендикулярна к направлению движения и будет лишь скользить.

Преобразование формулы P=R-U для вычислений. Ранее было указано, что при вычислении площадей дугу, на которую обернулся ободок счетного колеса, обыкновенно выражают в тысячных долях оборота. Обозначив, как и раньше, окружность ободка счетного колеса через С, 0,001 С через т и число тысячных долей, на к-рое обернулось колесо при обведении контура фигуры, через Ai, получим, что17=т-А*, следовательно P = R-r-n. Там же указано, что число тысячных долей, на которое обернулось колесо, получается как разность mz-mi отсчетов по циферблату, счетному колесу и верньеру до и после обведения контура, следовательно / = тпг -mj и

P = E .т(та-тп1). (15)

Множитель Rr есть произведение длины обводного рычага R на длину 0,001 С и представляет собой площадь прямоугольника, соответствующую тысячной доле оборота колеса, или цену одного деления П. Эту площадь можно рассматривать в ее натуральную величину в см, мм а вообще в тех единицах, в к-рых выражены Кит.

Пример. R =15,54 см, С =6,18 см, 0,001С=г = =0,00618 см (взяты с П. сист. Коради iNs 22927), следовательно

Rt=Po = 15,54 x 0,00618 = 0,096 cjvt2 = 9,6 лш .

Такое значение ро называют абсолютной ценой одного деления П. Зная эту цену, легко определить натуральную величину площади фигуры в тех единицах, в которых выражено ро- НороМ.б. придано другое значение. Построим на бумаге прямоугольник Ро по действительным величинам Д и т. Построенную площадь будем рассматривать как план некоторого земельного

участка, нанесенного в масштабе . При

составлении плана каждая линия местности уменьшается в М раз; и обратно, чтобы от площади плана иерейти к площади земельного участка, нуншо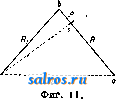

Фиг. 12.

ЛИНИИ плана увеличить в М раз. Увеличив R и г в М раз (фиг. 12), получил! другое значение для цены деления П., например So, выраженное в земельной мере. Ее называют относительной ценой одного деления П., следовательно

So=B - г М^. (16)

Числовое значениеро и обсть коэф. к ф-лы (13). Подставляя вместо Rr в формуле (15)

численную величину ро или So, будем получать площадь или в натуральную ее величину (в сж или мм) или в земельной мере (га или м^).

Определение численной величины цены делен ия П. Заменяя далее в ф-ле (15) Rr численным значением ро и о, получим две ф-лы:

р = Poimz - Wl) и Р = /So(w2 - Wl).

Первая ф-ла выражает площадь в натуральную ее величину, вторая-в единицах земельной меры. Отсюда

Ро=7~ и So=

тг-mi

следовательно для определения цены деления П. надо знать площадь в соответствующих единицах (р и Р) и соответствующее число делений П. (Wa-Wj), т. е. число тысячных долей оборота счетного колеса. На этом основании цена деления П. проще всего определяется опытным путем: строят на бумаге квадрат со сторонами в несколько см или дм., смотря по тому, в каких квадратных единицах будет выражаться площадь. Затем этот квадрат обводят несколько раз П. Из разностей отсчетов до и после обведения берут среднее, т. е. получают Wz-Wi. Разделив площадь квадрата на среднюю разность отсчетов, получают цену одного деления планиметра в натуральных единицах, т. е. в см или в дм.2

Пример. Построен квадрат со сторонами в 5 см. Площадь квадрата равна 25 см или 2 500 м.м^. Средняя разность отсчетов, выведенная из 5 обведений, равна 266 тысячных, или делений П. 25

Ро = cjn2 - 0,094 CMi =9,4 мм.

Для определения So площадь квадрата надо выразить в земельной мере, принимая во внимание масштаб-плана (ф-ла 16). Положим, что масштаб плана

т. е. 1 см соответствует 100 м, следовательно сторона квадрата будет равна 500 м, а его площадь 250 ООО или 25 га. Поэтому

25 250 ООО

So = -kx5 га = 0,094 га0,1 га; So = -;г-Jtt2 = 939,85 мК

266 то

Для увеличения точности обведение Hw делают несколько раз. Отдельные результаты (разности отсчетов) не должны отличаться более, чем на 1-2 деления. В таком случае за окончательный результат принимают среднее арифметическое. Самое обведение по сторонам квадрата следует делать по линейке (лучше по металлической), чтобы уменьшить сотрясение руки, искажающей отсчеты.

Контрольная линейка. К каждому П. прилагается небольшая линейка, к-рая помещается в его ящике. Эта линейка называется контрольной и служит для определения цены деления П. и вообще для его исследования. Контрольная линейка исключает необходимость построения геометрич. фигур для определения цены делений и позволяет быстро определять эту цену, уничтожая при этом сотрясение руки. Здесь описана контрольная линейка, нрилеженная к П. сист. Коради с постоянным рычагом за № 22927 и рассчитанная для определения цены деления П. для масштабов с прежним основанием (дюймовым). Но зная цену деления для масштаба с одним основанием, ее легко определить и для всякого

другого. Контрольная линейка, изображенная на фиг. 13 в плане и в разрезе,-металлическая, хорошо отполированная пластинка, длиной ок. 3,5 дм. Водном ееконцевстав-лена тонкая игла и, прикрытая винтом v. Другой ,конец линейки сточен под острие, на котором нарезан штрих t. Место, где вставлена цгда и, отмечено нулем. Начиная от него, через каждый дм. на поверхности линейки высверлены небольшие гнезда, отмеченные 1 , 2 , 3 . Во время работы линейку кладут на бумагу, в которую вдавливают иглу и. У другого конца линейки тонким карандашом проводят на бумаге черту

Фиг. 13.

т, с к-рой совмещают штрих линейки t. В гнездо, отстоящее от иглы на 1 , вставляют обводный шпиль, а П. примерно устанавливают так, как показано на фиг. 14, и делают отсчет, а затем, придерживая одной рукой обводный шпиль, чтобы он не вышел из гнезда, другой рукой осторожно двигают контрольную линейку по ходу часовой стрелки. Обведя полный круг, совмещают

штрих t с чертой т \ и снова делают от] счет. Т. о. обвод/ ный шпиль пройдет по окружности круга с радиусом в 1 . Окончив обведение, его надо повторить, но двигая П. уже в обратном направлении, т. е. против движения часовой стрелки. Подобным образом обводят круги с установкой обводного шпиля на 2 и на 3 . На основании изложенного будем иметь следующие формулы для определения цены деления с помощью контрольной линейки: если S-определяемая цена деления П., и mj-отсчеты до п после обведения круга с радуисом г=1 , пц и Шз-отсчеты для круга в 2г, Шд и Шд - отсчеты для круга в Зг, то

S(W2 - Wa) = я(2г)2 = 4яг2, S{m - W3) = jr(3r)2 = 9яг2,

Фиг. 14.

(16)

тп i-mi mj-m2 тз-тз

В следующей таблице приведены результаты определения цены деления П. сист. Коради с постоянным рьшагом № 22927 с установкой на контрольной линейке обводного шпиля на 1, 2 и 3 дм. Цена деления вычислена как для определения натуральной величины площади (в дм. 2), так и в земельной

мере, старой (в дес.) для масштаба и но-

еой (в га) для масштаба .

Определение цены деления П. дляразныхмасштабов. Выше при-

Средняя S: 3 0,093=0,09 га.

♦I 0,014 дм.г; *2 0,059 =0,06 дес;

ведена ф-ла, выражающая цену деления П. в земельной мере (ф-ла 16): So=R-r-M. Из нее видно, что So изменяется пропорционально изменению длины обводного рычага R и пропорционально квадрату знаменателя численного масштаба (т изменяться не может). Если измерять площади разньгх масштабов, но при одной и той же длине рычага й, то So будет зависеть только от масштаба. Если новый масштаб j, то для него цена деления будет Si=R-r-N. Взяв отношение равенстЕа,будем иметь откуда

-51= So 5,- (17)

Эта ф-ла позволяет цену деления, вычисленную для одного какого-либо масштаба, перечислить для произвольного.

Пример 1. Для Вычислить Si и S2 для масштабов

масштаба

So = 0,06 дес.

и

/4 200\2

4200 42 000

/42 000\2

= 1,5 дес.

Из этого примера видно, что знаменатель второго масштаба в 10 раз более знаменателя первого, а цена деления Sa более Si в 100 раз (М^).

Пример 2. Для масштаба So = 0.06 дес. Вычислить Si в метрич. мере для масштаба ~-

10001)

Пользуясь соотношением 1 дес.=1,09254 га, сначала надо перевести 0,06 дес. в га. Полученный результат

0,0655524 дает цену деления в га для масштаба - .

8400

Остается перечислить ее для масштаба

10000

Si = 0,06555 [) = 0,093 га;

получилась та же цена, к-рая вычислена ио контрольной линейке и помещена в предыдущей таблице.

Цена деления П. обыкновенно дается механиком для разных масштабов и при определенной длине обводного рьгаага. Результаты обычно пишутся на ярлыке, наклеенном внутри футляра П. Так, для П. № 22927 цены вычислены для Д=309,0 полумиллиметров. Цена деления м. б. вычислена непосредственно по ф-ле So=R-r-M, если известны размеры П. Так, для планиметра № 22927 при Д=6,16 дм. С=2,42 дм. и М-8 400, т =0,00242 дм.; М2=70 560 000hSo= = 6,16x0,00242x70 560 000 = 1 051 852 дм,2 По обращении в дес. So=0,0620,06 дес.

Вычислениевесьмамалыхпло-щ а д е й. При вычислении малых площадей.

большая цена деления дает и больший процент ошибки, поэтому выгоднее в таком случае, чтобы цена деления р, была возможно меньшей, а разность отсчетов /г. - , возможно большей. Но Ро =Rr, следовательно для >ту1еныиения p, надо уменьшить В. Если при длине рычага R цена деления была Ро, то для новой цены р^ рычаг надо изменить в R:

Po=R-r, Pi--Ri-t;

взяв отношение, будем иметь = . Из

этой пропорции получим

Po-Pi R-Ri

откуда R - Rj= R

Po-Pi

. По этой ф-ле вы-

числяется изменение длины рычага при изменении цены деления в другое.

Вычисление постоянного числа. При постановке полюса внутри фигуры ее площадь вычисляется по ф-ле: P=RU+Q или P=Solmi-mi) + Q. Если q-число делений П., соответствуюм1ее площади круга Q (So-цена одного деления П.). то предыдущая формула представится так: Р =So(mj - mi)--So , откуда

q = ~- (ma - mi).

too p

В 8T0M выражении --площадь фигуры в делениях

П., а (mj-mi)-разность отсчетов по П., когда его нолюс внутри фигуры.

Пример. Для определения q взят квадрат со

сторонами в 30 cjit; масштаб чертежа j следовательно сторона квадрата равна 3 000 м, а его площадь

Р 900

900 га. Цена деления П. So-0,09 га, член = =

оо

= 10 000 делений Разность отсчетов по П. wa-mi до и после обведения квадрата в среднем из 4 обведений равна 9 347, следовательно в = 10 ООО-(- 9 347) = 19 347 делений. Появление отрицательного знака у разности mj-mi объясняется тем, что площадь вычисляемого квадрата Р менее площади круга Q. В этом случае

счетное колесо при обведении II. будет вращаться в обратную сторону, мимо нуля верньера, подпись колеса будет проходить убывая, и второй отсчет та будет менее первого mi. Действительно, в ф-ле P=RU + Q, где все члены положительны, Q входит слагаемым. Разность P-Q=RV будет положительна и соответствует еространству между кругом Q и контуром (фиг. 15,а) к-рое П. обращает в пг>ямоугольник RU. Если Q более Р, то Р - Q = - hU. Но R отрицательным быть не может, и отрицательным будет U, т. е. ma-mi, и тогда mi>mj. Отрицательное К17 соответствует пространству между кругом и контуром на фиг. 15 6. Для получения численного значения-fit/ надо обводить П. против хода часовой ст()елки; в этом случае счетное колесо будет вращаться по возрастающей подписи, и второй отсчет та будет более первого mi. Приведенную выше ф-лу P=So(ma-mi)--Sog можно переписать так:

P = So[(maH-g)-mi]; вз нее видно, что при вычислении площади с постановкой полюса внутри фигуры надо ко второму отсчету прибавить число делений, соответствующее постоянному числу. Постоянное число в делениях П. также дается механиком для нек-рых масштабов и при определенной длине обводного рычага. Соответствующие числа написаны на ярлыке, наклеенном в футляре П.

Условия, требуемые от П.,и их поверка. Условия, требуемые от П., следующие: 1) счетное колесо должно свободно вращаться; 2) плоскость счетного колеса д. б. перпендикулярна к направлению обводного рычага; 3) длина обводного рычага

Фиг. 15.

Фиг. 16

должна соответствовать цене деления П., к-рая дана механиком; 4) постоянное число д. б. вычислено пг)авильно. При исследовании 1-го условия вращают счетное колесо около оси. Если вращение медленное, колесо будет останавливаться-ось слишком зажата. В этом случае положение оси надо изменить, действуя винтами при подшипниках. При вывинчивании подшипники будут ра.здвигаться, и вращение оси будет свободнее. При очень быстром вращении подшипники, наоборот, надо сдвинуть. При этом необходимо обратить внимание на то, чтобы счетное колесо не задевало верньера. Поверка 2-го условия, самого важного, производится так: измеряется площадь фигуры при двух положениях П.. к-1)ый устанавливают так. как показано на фиг. 16, т. е. счетное колесо в первый раз будет находиться влево, а во второй-вправо от линии,соединяющей полюс и обводный шпиль (линия РО). При обведении фигуры при обоих положениях П. делаются отсчеты, а их разности сравниваются между собой. Если разности отсчетов будут значительно различаться, то условие перпендикулярности не выполнено. Для исправления этого недостатка в П. системы Коради не сделано приспособлений. Но так как при указанных положениях П. счетное колесо будет занимать противоположные положения, то неправильность в положении колеса будет влиять на результат вычисления площади в разных направлениях и будет компенсироваться. Вследствие этого П. сист. Коради называют компенсационным. На этом основании можно рекомендовать производить вычисление площади при двух указанных положениях П. Среднее из результатов будет почти свободно от влияния этой ошибки. Поверка 3-го условия производится так. обр.: при помощи контрольной линейки вычисляется площадь круга. При этом свободный рычаг П. устанавливается на длину, указанную механиком. Обведение круга делается при двух положениях инструмента, указанных на фиг. 16. Для увеличения точности такое обведение следует повторить. Если разности отсчетов будут отличаться на 1-2 деления, то за окончательный результат принимают среднее. Умножив эту разность на цену деления П. So, данную механиком и соответствующую длине рычага, получают площадь круга по формуле P=So(Wa-Wi). Затем,вычислив площадь того же круга по ф-ле лг*, сравнивают с ней площадь, вьгаисленную П. Если площадь по П. будет более площади, вычисленной по формуле яг , то рычаг надо удлинить; если менее, то надо уменьшить. Это следует из того, что для одной и той нее площади RU=>BiUi, т. е. длины обводного рычага обратно пропорциональны длинам дуг, на которые обернулось счетное колесо. Следовательно для уменьшения длины дуги или соответствующей ей площади надо уве-

личить рычаг и наоборот. Изменение длины рычага м. б. рассчитано по ф-ле

Ri-R

здесь ц-число делений, вычисленное для

круга по ф-ле -, а /г,-разность отсчетов

ПО П. при установке его на длину рычага R.

Пример. R=3a24 полумиллиметра, =- = 2088

So

делениям, a<i=2 108 делениям, Bi - К = 332,1 -=

= 3,163,2 полумиллиметра. Т. к. площадь по пла-ниметруоказалась более геометрической, то рычаг надо увеличить, и ftj=335,3 полумилли.метра. Установив рычаг на новую длину, надо повторить испытание. Поверка постоянного, числа, вернее, числа делений q, соответствующего площади круга Q, производится так, как описано выше.

Некоторые замечания о пользовании П. 1) Надежные результаты П. дает, когда вычисляемая площадь начерчена на иовной, гладкой бумаге, без всяких шероховатостей. Неровная бумага влияет на обороты счетного колеса и искажает отсчеты. 2) Не следует делать начальный отсчет нулем, а лучше записать его так, как указывает инструмент. При установке на нуль можно не заметить 1-2 делений, на к-[1ые отойдет счетное колесо. 3) Когда указатель на циферблате находится близ какой-либо цифры, то надо об)атить внимание на положение нуля верньера относительно штрихов счетного колеса, подписанных 9 (девяткой), о (нулем) и 1 (единицей). Если нуль верньера находится между 9 и О колеса, то с циферблата надо взять меньшую цифру,- если он находится между О и 1, то надо записать ту, на к-рую указывает индекс. 4) Обводный шпиль надо двигать по контуру осторожно, выбирая все извплины, следя в то же время ва движением циферблата. Если при обведении контура по ходу часовой стрелки нуль циферблата прошел мимо указателя нессолько раз, то столько же раз ко второму отсчету прибавляется 10 ООО; при обратном движении эта цифра вычитается. 5) Обведение контура надо делать не менее двух раз в прямом и обратном направлениях и при двух положениях планиметра. 6) П|1И вычислении Majujx площадей выгоднее брать рычаг короче.

Точность вычисления площадей П. зависит от многих условий. На нее влияет качество плана, форма контура, величина площади и пр. Изменение площадей по старым планам, бумага к-рых измята, менее надежно. Также невыгодно вьгаислять П. узкие и длинные полосы, дороги, просеки, канавы, лесные делянки и пр. Площади таких полос точнее вычислять по натуральным измерениям. Малые площади вычисляются с большей ошибкой. Практика показывает, что при наивыгоднейших условиях измерение площадей П. сист. Коради при двух положениях инструмента производится с ошибкой до 0,0025 или ( -) изме-

\ 400/

ряемой площади. Механик Коради ввел усовершенствование в своем компенсащ10нном П., поместив счетное колесо на особую шайбу, сделанную из твердого каучука и

Фиг. 17.

гладко отполированную; благодаря этому на отсчетах по колесу не сказываются неровности бумаги (фиг. 17). с. Цветиоа.

Б. Наиболее совершенным из линей-н ы X П. является линейный П. с шаровым сегментом сист. Гомана- Коради (фиг. 18). Он состоит из рамы А А, в к-рой вращается

ось с наглухо приделанньми к ней двумя тяжелыми валиками ВВ равных диаметров так что при передвижении прибора по бумаге он сохраняет неизменное направление.. Параллельно оси валиков ВВ в верхней части рамы расположена другая ось с зубчатым колесиком и тщательно выгочеиньню шаровым сегментом е, прикасаюхшшся к совершенно гладкому полированиму цилинд-

Фиг. 18.

ру Е, целые обороты которого отсчитьшаются на циферблате F. а части оборота по верньеру на барабане G. Наружные поверхности валиков ВВ нарезаны мелкими зубцами (насечками), так что валики могут только катиться, но не скользить по бумаге; зубцы левого валика В захватывают зубцы зубчатого колеса оси вращения сегмента е, и потому во время движения прибора на бумаге вращаются как валики ВВ, так и ось сегмента е; соприкасаясь с поверхностью пи-линдра Е, шаровой сегмент е вращает цилиндр Е. Если зубцы валиков и зубчатого^ колеса оси сегмента е одинаковы, то длина дуги, на к-рую обернется валик В, равна общей длине дуги всех одновременных оборотов оси сегмента е; иначе говоря, линейное-перемещение всего прибора по направлению, перпендикулярному к оси валиков ВВ, равно линейному перемещению какой-либО точки окружности оси сечении е. В середине рамы АА расположена вертикальная ось^ около к-рой может' поворачиваться вправо и влево в известных пределах обоймипа а;, в верхней части этой обоймицы помещен упомянутый выше гладкий цилиндр Е, а внизу вставлен длинный брусок R (рычаг> с ведущим острием М на конце. Брусок разделен по всей своей длине на мм и при помощи небольшой обоймицы с верньером, зажимным винтом b и гайкой с м. б. поставлен и закреплен в любой части своей длины, для чего он вдвигается в обоймицу или вьщвигается из нее. Ведущее острие М составляет третью точку опоры инструмента во время измерения площади; но две другие-точки опоры (валики ВВ) расположены так, что ц. т. всей системы находится почти над ними и давление на ведущее остриеМ незначительно. Оси цилиндра Е и бруска (рычага> R всегда параллельны, причем цилиндр Е особой пружиною в обоймице постоянно нажимается на шаровой сегмент е и, смотря по положению обоймицы а, зависящей от-движения ведущего острия вправо или влево, касается сегмента в разных точках. Когда ось рычага R перпендикулярна к оси валиков ВВ, тогда цилиндр Е касается вершины сегмента и остается неподвижным, хотя бы П. двигался и сегмент вращался..

Если рычаг повернуть вправо, то цилиндр Е касается сегмента в точке, расноложен-шой ближе к барабану G, и при двинении П. ©перед вращается в сторону возрастающих адписей циферблата и барабана; наоборот, если рычаг R повернуть влево, то цилиндр Е коснется сегмента в точке, более удаленной от барабана G, и при том же иаправле-нки движения П. будет вращаться в сторону уменьшающихся надписей. Чем больше повернуты рычаг и цилиндр, тем точка касания цилиндра к сегменту более удалена от ершины сегмента, и тем следовательно скорее вращается цилиндр при той же скорости поступательного движения П.

Теория этого П. дает следующую ф-лу: Р = C{N - п), где Р-измеряемая площадь, С-нек-рое по- стоянное число, зависящее от размеров П., N-отсчет по циферблату, барабану и вер-яьеру после обвода фигуры, п-отсчет перед обводом этой фигуры. Постоянная величина С м. б. вь1числена по измерению отдельных частей П., но это не точно; точнее и скорее определить ее из опыта, обводом какой-ни--будь простой геометрич. фигуры известной площади, напр. круга или квадрата. Зиая площадь такой фигуры и отсчеты при на-чале и конце обвода, получим:

Постоянную с можно изменить, вдвигая и .выдвигая рычаг R. Для широких площадей можно вставить дополнительное колено. Т. к. рычаг и дополнительное его колено имеют мелкие деления, то, определив С при JIB ух разных установках (длинах) рычага, .1:ожно вычислить по пропорции ту установку, при к-рой постоянная С будет круглым числом или числом, выражающим пло-яцадь в или в других мерах при данном масштабе плана (чертежа).

Для измерения площади описанным П. <5тавятесо на чертеж так, чтобы ось валиков ВВ приняла направление, перпендикуляр-щое к длинной средней линии обводимой фигуры, и чтобы отклонения рычага с ведущим острием в ту и другую стороны были достаточны для обвода но всем извилинам контура. Затем, установив острие М в любую точку контура, отмечаемую накол ом тонкой иглы или же тонко очинённого карандаша, делают отсчет по циферблату, барабану и зверньеру; после этого обводят контур острижем в сторону вращения часовой стрелки, пока острие не вернется в начальную замеченную точку, и делают второй отсчет. Раз-юность отсчетов, помноженная на постоян-:Ное число, даст площадь обведенной фигуры в мелких или земельных мерах.

К линейным П. можно отнести линейку-планиметр Зарубина (фиг. 19: А-профиль, Б-план). Она состоит из двух -частей: линейки и счетного механизма. Линейка LL имеет на обоих своих концах по прямоугольному вырезу тп, в которых вращаются на общей оси 00 два одинакового диаметра валика а с рубчатой поверх-шостью. Концы оси помещаются в стойках К п К', к-рые привинчены к линейке; для уменьшения трения в концы оси 00 (в ко-

нические в них углубления) входят конические острия, вделанные в стойки К и К' и составляющие с ними одно целое. Для удобства прокатывания линейки по бумаге, на к-рой начерчен контур, на ее концах сделаны две рукоятки д, д. Сверху ось и валик

Же

1кв о

Фиг. 19.

прикрыты полым медным полуцилиндром D. Счетный механизм (фиг. 20: А-вертикальный разрез, Б-план) устроен след. образом: конец b оси валиков аа снабжен шестерней е, передающей своими зубцами вращательное движение зубчатому коронному колесу р, соединенному наглухо с его вертикальною осью вращения, утвержденной нижним концом в линейке, а в средней части в стойке-скобе, снизу привинченной к линейке. На верхний конец оси коронного колеса насажена большая стрелка б, вращающаяся по большому внешнему кругу

Фиг. 20.

циферблата Z, Для подсчета полных оборотов большой стрелки б над циферблатом имеется другая, малая стрелка м, движущаяся по внутреннему кругу, концентрическому с первым. Внешний круг разделен на 100 частей, подпись идет слева направо через каждые 10 делений; внутренний круг имеет 50 делений. Малая стрелка движется в 50 раз медленней большой, что достигается системою зубчатых колес, передающей движение большой стрелки б малой стрелке j t. Вследствие равенства диаметров валиков скошенньгй край линейки L при движении планиметра перемещается параллельно самому себе. Из устройства П. ясно, что число оборотов валиков, помноженное на длину окружности валика выраясает длину пути, пройденного П. по бумаге.

Применение П. состоит в том, что фигуру, площадь к-рий надо измерить, превращают известгыми геометрич. приемами в равновеликий треугольник (или трапецию); .затем прикла:1ывают скошенный край линейки П. к основанию тр-ка и делают отсчет и; затем прокатывают П. настолько, чтобы вершина тр-ка находилась на скошенном крае, делают второй отсчет п'; разность отсчетов п'-п, помноженная на длину окружности валика, выраженную в тех или иных мерах длины, даст длину высоты тр-ка, следовательно и половину ее длины; помножив ниловину высоты на длину основания, получим площадь тр-ка, равновеликого площади фигуры. Для