 |
 |
 |
 |
1 2 3 4 5 6 7 8 ... 49 иногда значительной сложности устройства (фиг. 37). При ряжевых опорах специальных ледорезов обьшно не устраивают; ро.ль их играет режущее ребро быков, к-рое в необходимых случаях соответственно усиливают. О. м. подвижных имеют ряд особенностей, всецело обусловливаемых системой и конструкцией пролетного строения моста. Так например, опоры разводных мостов в большинстве случаев получают значительное развитие, необходимое для размещения на них устройств и механизмов для разведения моста. Таковы например: круглый бык в двухрукавных по-воротныхмостах (фиг. 38); быки раскрывающихся мостов с обширными полостями для помещения опускающихся концов подъемных рукавов моста {фиг. 39); устои однору-кавных поворотных мостов, сильно развитые вдоль и поперек моста д.т:я помещения короткого хвоста пролетного строения и устройства пут его перемещения <фиг. 40). Для облегчения опор при значительной ширине мостов в теле их обыкновенно устраивают пустоты; круглые быки с этой целью устраивают не сплошными, но кольцеобразными, с продольными и с поперечными стенками и перекрытием образующихся колодцев жел.-бет. конструкцией. Опоры наплавных мостов, устои и про-межлточные опоры,резко отличаются друг от друга. Устройство неподвижных устоев, каменных или деревянных, не представляет значительных особенностей; подвижные промежуточные опоры вполне своеобразны. В простейшем типе наплавных мостов-п л от о в ы X, промежуточные опоры являются составленными из одного или нескольких рядов бревен или брусьев плотами, взаимно связанными между собой канатами и лежа-пщм на них ездовым полотном моста (фиг. 41); на месте они удерживаются при помощи якорей. В плашкоутных мостах про-меж^точными опорами служат деревянные понтоны, пример устройства к-рых приведен на фиг. 42. Применение металлических, а в последнее время и железобетонных, понтонов (см.) встречается значительно реже. Размеры 0. м. Основные размеры опор определяются расчетом в предпотожении действия на опору наиболее невыгодной из всех возмонньгх комбинаций внешних сил (нагрузок). Внешние силы, которые действуют на О. мостов, следующие: 1) собственный вес, 2) реакции пролетного строения моста. 3) подвижная нагрузка (поезд, экипажи, толпа людей), 4) давление земляной насьши как горизонтальное, так и вертикальное (на подземные выступы опор), 5) давление ветра, 6) тормозная сила и 7) центробежная сила. 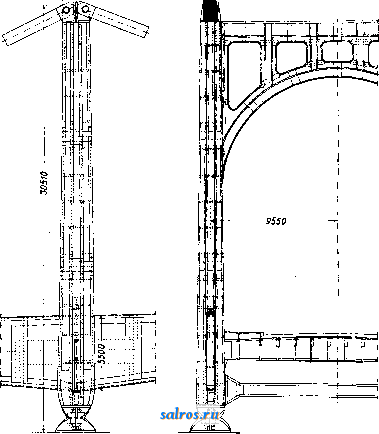 -3000- Фиг. 22. Первые 4 силы, а также тормозная сила, вводятся в;расчет как устоев, так и быков; давление ветра и центробежная сила-исключительно в расчет быков, причем две последние силы (тормозная и центробен^ная)  только в расчет опор ж.-д. мостов. Все внешние силы м. б. подразделены на две группы: основные силы, т. е. такие, к-рые действуют на опору постоянно и возникают при каждом проходе нагрузки по мосту; к этой группе относятся: собственный вес опоры и пролетного строения, подвижная нагрузка, давление земляной засьшки и центробежная сила; во вторую группу входят так называемые случайные силы, к которым относятся давление ветра и тормозная сила. Собственный вес опор принимается при расчете по дей- строения моста. При этом при расчете под-ферменных камней и прокладных рядов под ними или соответ-ствуюпгих им частей опор вес подвижной нагрузки увеличивается на динамическую добав-   Фиг. 24. ствительному их весу. Реакции пролетного строения, сводящиеся для балочных мостов к весу его, а в арочных и в висячих вклю- фиг. 25. ку, величина которой определяется по нормам, установленным дли расчета;; пролетного строения моста (металлического, же-   Фиг. 2 6. чающие кроме того распор, принимаются согласно расчету пролетного строения. Вес 11 I 111 11 ITTTT    Фиг. 27. подвижной нагрузки принимается по нормам, установленным для расчета пролетного лезобетонного или каменного). Горизонтальное давление земли учитывается при расчете устоев и береговых бьпсов. В расчет сквозных опор (напр. деревянных свайных) оно не вводится по незначительности его. Величина этого давления опреде.тяется по общей теории расчета тЬпьр'шх стенок; (см.) в предположении, что 1) трение грунта; по поверхности опоры отсутствует, 2) сцепление между частицами грунта не имеет места, 3) поверхность скольжения призмы обрушения есть плоскость и 4) давление земли на внутреннюю вертикальную грань опоры направлено горизонтально. При этих: условиях давление земли на глубине Н от поверхности засьшки при ограничении поверхности насьши за устоем горизонтальной плоскостью, что всегда имеет место в опоре мостов, определится по следующей; формуле: где у-вес единицы объема грунта, tp-угол естественного откоса засьшки (угол внутреннего трения). Если опора заложена в грунте, не способном оказьшать бокового давления, т. е. угол к-рого равен или близок к 90° (напр. скала, сухая твердая глина) то за величину Н принимается расстояние от поверхности насыпи до верхней поверхности этого грунта. При расчете береговых быков величина Я измеряется отуровняесте-ственного грунта или размытого дна, причем, если бык заложен в достаточно плотном, грунте, напр. в глине, песке, то Н принимается не больше 10 ж; на глубине свыше Юм давление считается равномерно распределенным по плопдади сечения опоры. Если бык заложен в слабом грунте, то за Н принимается полная глубина заложения опоры до сечения на границе слабого и нижележащего плотного грунта. Точка приложения силы в СССР Единых норм строительного проектирования , утвержденных 14 марта 1930 г., изменяющимся по определенному закону по высоте опоры. Низший предел этого давления зависит от соотношения размеров  -f-<?<7 /,20 Фиг. 28. Е находится на расстоянии / Н от поверхности грунта (для устоев-насыпи). Нагрузка, находящаяся на насьши за устоем (например поезд), производит дополнительное горизонтальное давление на устой, величина к-рого выражается ф-лой: £;i = yH/htg2(45°-), а момент относительно сечения на глубине В ф-лой: Mi = lrH%tg2(45°-). Здесь б/г; /1 = 4-. Коэф-ты а и j8, характеризующие постепенное уменьшение воздействия иа опору нагрузки на насьши с увеличением глубины  Фиг. 30. Я, определяются по особым таблицам; Q- полный вес нагрузки, находящейся на призме обрушения; I-длина призмы обрушения; и-ширина поперек моста полосы, занятой нагрузкой на насыпи; для ж.-д. мостов а принимается равной длине шпалы. Давление ветра приш1мается действующим горизонтально и, согласно недавно введенных Фиг. 29. (ширины И длины) и формы сечения опоры и колеблется от 110 до 165 з/ж*; высший может быть не более 225 кг/л1*. Для жел.-дор. мостов при наличии поезда на мосту высший предел давления ветра^обык-новенно принимается равньш 130 кг/м^  Фиг, 31. что соответствует условию равновесия порожнего нормального товарного вагона. Тормозная сила, вводимая, как сказано, в расчет опор только ж.-д. мостов, определяется по формуле: Т=0,15 (i;P-bO,25 SQ), где^Р- вес паровозов с тендерами и -вес вагонов. Сила эта направлена горизонтально и считается приложенной: от поезда, нахо-  Фиг. 32. дящегося на пролетном строении моста, в центре шарнира опорных частей или в случае плоских и тангенциальньгх онор - на уровне верха нижней опорной подушки или  5,62 Фиг. 33. опорного листа; от части поезда, находящейся на устое,--к головке рельса и от части поезда на призме обрушения-на середине высоты призмы обрушения. Кроме того в мостах Скобы Фиг. 34. С ездой поверху обьжновенно вводится еще в расчет возникающая при торможении перегрузка передней по направлению движения и разгрузка задней опоры. Величина этой перегрузки выражается ф-лой: S=, где h-расстояние от ц. т. поезда (принимаемого на высоте 2 м над головкой рельса до центра  фиг. 35. шарнира опорной части, Z-расчетный пролет моста. Сила торможения оказывает существенное влияние на увеличение размеров Разрез по СО 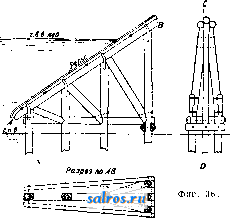 о. м. при малых и средних пролетах, т. е. в громадном большинстве случаев практики. Поэтому при проектировании моста следует 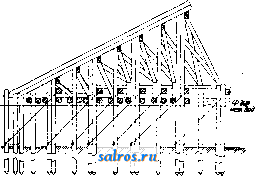 Фиг. 37. принимать во внимание фактич. возможность торможения в зависимости от условий профиля Линии, расположения моста по отно- 7154 19�1499145954993 шению к станции и т. п. и в тех случаях, когда это возможно, или вовсе не вводить в расчет опор торможения, напр, при односто-  Фиг. 38. роннем движении и расположении моста на предельном подъеме, или считаться с возможностью торможения только при определенном направлении движения. Центробежная сила принимается равной /ю эквивалентной нагрузки (по перерезьшающей силе) на обоих опирающихся на бьш пролетных строениях. Точка ее приложения считается в центре тяжести поезда (на 2 м вьппе головки рельса). Допускаемые напряжения на различного рода материал опор принимаются в СССР согласно упомянутым .Единым нормам строительного проектирования . Для каменной кладки величина этих норм установлена в зависимости от временного сопротивления камня, идущего на кладку, и качества применяемого раствора и колеблется в довольно широких пределах. Общие принщты этих норм сводятся к следующему: допускаемое напряжение на сжатие при изгибе, яв-.дяющееся основньпй напряжением, принимается от Vao временного сопротивления камня при тощих растворах до Vio при жирных растворах. Производные напряжения составляют: на осевое сжатие 0,8, на растяжение при изгибе 0,12 и на скалывание 0,1 от основного. , Эти допускаемые напряжения установлены для случая действия одних только основных сил; при совместном действии основных и случайных си.д допускаемые напряжения повышаются на 30%. Напряжение на растяжение во всяком случае нельзя допускать > 5кг/сл**. При расчете высоких тонких опор учитывается возможность продольного изгиба путем умножения расчетных нагрузок при т. 9. т. XV. определении сжатия на некоторый коэф-т больший единицы. Допускаемые напряженная в опорах из всякого рода др. материалов: бетона, железобетона, металла и дерева принимаются установленные для пролетных строений мостов из тех же материалов. Выбор типа и материала 0. м. Тип и материал О. м. определяется назначением моста, системой его пролетного строения, предусматриваемым сроком его службы, а также местными условиями, каковы режим пере-крьшаемого водного потока, высота опор,  Фиг. 39. характер грунта, наличие материалов, необходимых для возведения опор (камень, лес), специальньши технич. требованиями и наконец требованиями общей экономичности сооружения. Деревянные опоры по самому свойству материала без принятия специальных предохранительных мер недолговечны; поэтому они вообще уместны только в мостах временного характера или при необходимости быстрого возведения сооружения, 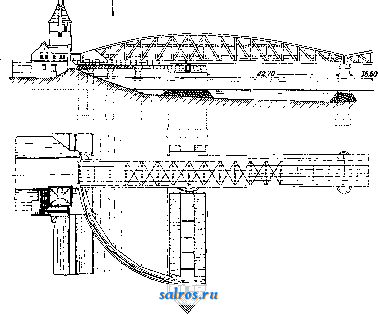 ФИГ. 40. в особенности при слабых малонадежных грунтах в основании опор, а также в других подобных случаях. Деревянные опоры в громадном большинстве применяются при де- ревянном же пролетном строении моста, величина пролетов к-рых редко превосходит 40 м. Это ставит предел выгодности применения деревянных опор по высоте. Предел этот для мостов подкосно-балочной системы лежит ок. 12-15.ле. Для сквозных пролетных 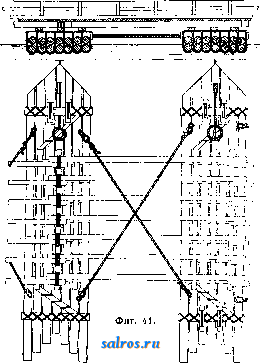  фиг. 42. строений известны случаи (гл. обр. в Америке) устройства деревянных онор до 50 и и даже 60 м высотой; но это является только исключениями. Область применения жел.-бет. опор, сравнительно дорогих, ограничивается гл. оор. случаями сооружения мостов на слабых грунтах, давая возможность путем устройства опор пустотелыми и т. п. 8начите.71ьно их облегчить и тем существенно понизить давление ца основание. Жел.-бет. опоры рамного тина, целесообразные главным образом при легких нагрузках в мостах под обыкновенную дорогу, успешно конкурируют в этих случаях с металлическими и каменными. Сфера применения металлич. опор была уже указана при описании их типов. Сравнительная дороговизна этих опор ставит предел расширению области их применения. Каменные опоры являются наиболее распространенным видом опор в мостостроении. Дешевизна и повсеместное распро- странение основного материала опор-камня, солидность и простота конструкции и долговечность службы делают применение их в громадном большинстве случаев технически и экономически наиболее целесообразным. При больших высотах моста вес каменных опор, несмотря на всевозможные меры к облегчению их, сильно возрастает. Здесь в связи с могущим быть допущенным давлением на грунт в основании опор лежит предел выгодности применения каменных опор. Правда, благодаря широкому распространению в настоящее время применения сжатого воздуха и других современных приемов для устройства глубоких искусственных оснований опор, предел этот значительно повысился, но все же очень высокие опоры, напр. пилоны висячих мостов, делаются каменными обьгано только в тех случаях, когда они м. б. заложены на скале; при других условиях грунта выгоднее переходить к легким металлич. опорам. М. холщевников. Лит.: см. Мосты. ОПРЕДЕЛИТЕЛ И, д е т е р м и и а и т ы, алгебраические суммы, образованные по особому правилу из каких-нибудь количеств (чисел, независимых переменных, функций и т. п.); такого рода суммы часто встречаются в различных отраслях математики, поэтому для этих сумм введено и особое название и схематич. обозначение, удобное для запоминания, преобразований и вычислений. Возьмем систему напр. трех ур-ий с тремя неизвестными: сцж + ъ^у + cz = ал а^х + Ъ^у -\-с^2=йЛ- (1) а^х Л- Ъ^у 4- Сз0= daJ Решение:
0123 -оцЬзСг + 26301 -02163 + ОзЬхСг- abzCi В выражениях (2) для неизвестных ж, 2/и 2 знаменатели одинаковы, числители же, как легко заметить, получаются из знаменателя через замену коэфициентов, при определяемом неизвестном, количествами правой части ур-ий. А.пгебраич. суймы, стоящие в числителе и знаменателе ф-л (2), и являются определителями. Следуя общепринятому обозначению для О. (Cayley), записывают например знаменатель в выражении (2) так: % bj Ci 0,2 bz С2 (3) 3 3 3 Про О. (3) говорят, что он образован из трех горизонталей и трех вертикалей, и называют О. третьего порядка. Итак имеет место тождество: ai &1 Ci ttg 2 = ClibzCa - х^зСг + а^Ь^С^ - аз Ьз Сз - aaiCa -f- а^Ъ^с^ - а^Ъ^с^. (4) Девять количеств, записанных схематически в левой части тождества (4), называются элементами О., а шесть слагаемых правой части-ч ленами О. Укажем нек-рые применения О. третьего порядка.Площадь тр-ка с вершинами(ж1,2/1). (Xi, У2), (Xz, ijs) в прямоугольной системе координат равняется: Xi Vi 1 , 8 1 Ур-ие прямой, проходящей через две данные точки (Ж1, iji) и (Жа, у^у. X у 1 Ж] 2/11 = О. Жа 2/21 В векторном исчислении векторное произведение [АВ] выражается О. 3-го порядка: i J Тс А^ Ау Ag By Bg где А^, Ау, Ag и В^, By, В^ - проекции соответственно векторов А я JB на. прямоугольные оси координат, а *, j и к-единичные векторы на тех же осях. Механика, трактующая свое содерлсаиие на базе векторного исчисления, пользуется О. 3-го порядка; напр. момент М силы F г секториальная скорость У У 7с линейная скорость в зависимости от угловой и выразится так: * 3 Тс м„ м„ м V = [иг] = X у Z и т. п. в тензорном исчислении удобно пользоваться схемой записи О. 3-го порядка, налож;ив нек-рые ограничения при преобразованиях с О. Так, тензор Т, имеющий составляющими tti, &1, Ci; tta, Ъ^, Са; Og, bg, Cg, представится в виде условного равенства 1 Ьг Сг Т - I а, Ьа Са обратный тензор т-1 = а, Ъо с. 2 2 С2 al b Ca причем составляющие этого тензора
tta b 1*1 t/i Ci 2 2 Ca 3 C3 -T и T. Д. Введем более удобную для общих заключений систему записи элементов О. при помощи двойных индексов с таким расчетом, чтобы первый индекс при букве указывал пор^док горизонтали, а второй-порядок вертикали. При такой записи мы обойдемся очевидно только одной буквой, и равенство (4) принимает вид: % (Нг 13 ttai 22 23 31 ttga СЬзз - tt2ii2<*33 + З1 1а аз siaais или, переставляя в правой части тождества множители так, чтобы первые индексы следовали в натуральном порядке, имеем: 11 12 13 21 22 23 31 82 33 , + aiaaaiOtaa - ia 2i 3s + 12 2з з1 - 1з 22 з1- (5) В правой части тождества (5) каждое слагаемое имеет вид: ± aiaay, где а, р, у представляют любую перестановку натуральных чисел 1, 2, 3; знак + берется в том случае, если числа а,р,у образуют четное число инверсий (см.), знак - в противоположном случае. Очевидно число членов О. 3-го порядка будет 3!. Возьмем 71 количеств, расположенных в виде квадратной таблицы: 11 12 13 21 Я22 23 Wl 112 3 = 2(-1)Ча, 2Аз-. а,-(8) Составим произведение из п множителей, взятых по одному из каждой горизонтали нашей таблицы: 1а1 2а, 3аз , вторые индексы а^, а^, а„ представляют нек-рую перестановку из чисел 1,2,3, ..., м. Условимся брать произведение (7) со знаком (-1), где к-число инверсий в перестановке 1 Са ... а„. Алгебраич. сумхму слагаемых вида (-1)Ча, 2аа распространенную на всевозможные перестановки а j Са.-.а из п элементов 1,2,3, называют О. п-то порядка и записывают так: и 12 1 21 22 2 1 J12 я О. w-ro порядка имеет п горизонталей и п вертикалей; количеств aj, записанных схематически в левой части тождества (8), называются элементами О., а слагаемые правой части - членами О. Очевидно О. п-то порядка имеет п\ членов. Правая часть тождества (8)дает краткую запись разложения О. те-го порядка. Таблицу (6), состоящую из п горизонталей и п вертикалей, называют матрицей квадратной в том смы-сде, что она порождает О. п-то порядка; числа называются элементами матрицы. Мат-трица м. б. п не квадратной, а состоять из тп чисел: 11 12 1Н 21 22 2н 5 г1 (2 )н пусть например п> т, тогда из матрицы (6) можно образовать О. наибольшего порядка т. Очевидно таких О. мояшо составить числом Может случиться, что все О. порядков т-го, (ш -1)-го, (т -2)-го, (р-Ь1)-го равны нулю, но из О. р-го порядка по крайней мере один не равен нулю. В таком случае, следуя Кронекеру,говорят, что матрица (6) имеет так называемый ранг р или характеристику р. Приведем нек-рые элементарные свойства О.: 1) О. не изменяет своей величины, если превратить горизонтали в соответствующие вертикали, и наоборот; 2) О. сохраняет абсолютную величину, но излхеняет знак, если в нем переставить два параллельных ряда(т.е. две горизонтали или две вертикали); 3) О. равен нулю, если два его параллельных ряда равны между собою; 4) если все элементы одного ряда О. умножить на число к, то и О. помножится на это число fc; 5) О. не изменяет своей величины, если ко всем элементам какого-либо ряда прибавить соответствующие элементы параллельного ряда, умноженные на произвольное число 1\ б) если элементы двух параллельных рядов О. соответственно пропорциональны, то О. равен нулю. На основе этих свойств обычно производят преобразования и вычисления О. Теорема сложения О.: 12 dxn 21 22 2п 11 12 21 22 1 22 . а т , им И 12 21 22 2И I ., Теорема у.множения О. (Бин?-Коши):
п1 от Сц Ci2 ... Ci С21 С22 ... С^п (10) ... Су, где Cij равняется или 1) ttiibij -Ь ttzibj + ... + dmnj (комбинирова гае вертикалей множимого с вертикалями множителя),
ИЛИ 2) a/i>ji + aabji + (гориз нтати с горизонталями), или 3) aubj-L + а^гЪр + ... + aibjn (вер!икали с горизонталями), или 4) ,ii; + aibj + ... + ainbnj (горизонтали с вертикалями); напр. по 3) имеем: ll&ll-f 2ibi2 llb2l + 2lb22 12ll+ 2212 12b21+aa2b22 1111 + 12&21 llbi2 + 1222 j 21 11 + 2221 2112 + 2222 1 Легко проверить, что оба произведения равны друг другу. Если в О. п-го порядка вычеркнем m горизонталей и столько же вертикалей и сдвинем остальные ряды, не изменяя их расположения, то получим новый О. М (п-туто порядка, называемый минором данного. С другой стороны, из вычеркнутых горизон-та.пей и вертикалей образуется О. М' т-то порядка, к-рый называется дополнением минора М. Очевидно и наоборот: М яв- ляется дополнением минора М'. Например 11 12 13 14 16 21 22 28 24 25 31 32 33 84 35 I (11) 41 42 48 44 45 61 62 53 64 65 вычеркнем в О. 5-го порядка вторую и третью горизонтали и третью и пятую вертикали; тогда оставшиеся элементы дают О. 3-го порядка-минор 11 12 14 41 42 44 61 52 54 ДЛЯ о. (11), а на пересечении вычеркнутых рядов получается О. 2-го порядка-дополнение минора (12): 23 25 83 35 Очевидно и обратно: О. (12) является дополнением минора (13). Если дополнение минора М взять со знаком (-l) * ®, где S-сумма порядков вычеркнутых горизонталей, а S-сумма порядка вычеркнутых вертикалей, то получим так называемое алгебраическое донолнение минора М. В наш^м примере минор (12) имеет алгеб-раич. дополнением (12) (13) 23 25 88 35 Элементы О. сами м. б. рассматриваемы как миноры 1-го порядка. Для получения алгебраического дополнения элемента j- j надо вычеркнуть г-ю горизонталь и j-io вертикаль, из оставшихся рядов образовать минор и взять его со знаком (-1)*+. Если обозначим через A{j алгебраич. дополнение элемента aij, то суммы гИJ1 + a 2j2 + . . 4- ш^Jn и ctii-ij + o,2i2j + + aiAnj равны значению О., если i=j, и равны нулю, если i=j (Везу). Например: 11 12 13 21 22 23 31 32 33 = 11.411 + 1212 + 1зЛ8. где 11=(-1) 22 2 82 3 , Л2=(-1/ 21 23 31 33 Аз = (-1) 21 22 31 32 В этом случае говорят, что О. разложен по элементам горизонтали (первой). Еще пример: разлагая по элементам первой вертикали, легко проверить тождество: о 1 2 -1 -1 о ... о о О -1 ж ... О О О О О ... ж О О О О ... -1 ж = оЖ + 1Ж -1 + 2ж -2 + ... -f . Укажем некоторые нрилолсения О. п-то порядка. Обрахимся к системе п линейных ур-ий с W неизвестными, решение и исследование которой в сущности и послужило при- чиной возникновения теории О. Имеем: aaii + а^гХг + ... + аЛ = 2 (14) Определитель и 12 31 22 1 а называется О. системы ур-ий (14). Умножая первое уравнение системы на алгебраич. дополнение элемента а^., второе-на алгебраич. дополнение gj. элемента а^к и т. д., наконец последнее на алгебраич. дополнение JL j элемента а^, и складывая почленно результаты, находим: BxD, (14) где -О., получаемый из D через замену в нем элементов' /с-й вертикали вторыми частями ур-ий. Полагая в ур-ии (14) =1, 2,..., п и считая DO, получаем решение системы: -1 - д 2 - . 1 -П - £> Отличие от нуля О. В является необходимым и достаточным условием, чтобы система п линейных ур-1)й с п неизвестными илхела единственное решение. Полагая в системе (14) bi=ba=...=6=0, получаем систему однородных линейных ур-ий. В этом случае ур-ие (14) обратится в Dxk = О, откуда видно, что обрашение О. 1> в нуль есть необходимое условие сушествоваиия решения, среди к-рого не все значения неизвестных равняются нулю. Приложения в геометрии: ур-ие плоскости, проходяшей че-оез три данные точки (oi, Ух, Zi), {х^,Уг- г^), fe> Уз, з): \х у Z 1 Xi у^ Zx 1 Жа У 2 2 1 Хг Ул 1 Ур-ие кривой второго порядка, проходяшей через пять данных точек (Жг, у-, (жа, у^, ... (Жв, 2/5), выражается О. 5-го порядка: х' X у у^ X у 1 х1 Ж1 у1 Ж1 2/1 1 = 0. = 0. х^ Ж5 2/5 У1 Хъ 2/5 1 Объем тетраэдра в ф-ии координат его вершин равен Хх Ух Ч 1 Жа 2/2 2 1 Xz Уз 3 Xi 2/4 4 1 Определите.яи широко применяются в теории линейных и квадратичных форм. Большую роль в теории О. играет так наз. теорема Лапласа: О. w-ro порядка равен сумме произведений из всех различных миноров, заключаюшихся вт горизонталях или вертикалях (mn), на алгебраические дополнения этих миноров (мы не приводим этой теорелты в другой обобщенной редакции Коши). Имеется аналогия между теоремой Везу и теоремой Лапласа: если разложение по первой теореме сводит вычисление О. w-ro порядки к вычислению п О. (w -1)-го порядка, то разложение по теореме Лапласа значительно понижает порядок О., но зато увеличивает число их. Так напр., вычисление О. 5-го порядка по теореме Везу сводится к вычислению пяти О. 4-го порядка, между тем как по теореме Лапласа вычисление того же О. может быть сведено к вычислению десяти О. 2-го порядка и стольких же О. 3-го порядка. Рассмотрим нек-рые специальные О. Пусть 11 1 21 22 - 2 и1 па ... ,! Заменим элементы этого О. алгебраич. до- полнениями их: 11 13 -4ai А22 -хп ... D я А называются взаимными (rezip-гоке Determinante). Умнонсая D на J, получаем: 1> О 0...0 О D 0...0 О 0 0...D zl=D -i (D=0). Легко показать, что при Z> = О и = 0. Если в О. D aij=aji, то такой О. называется симметрическим. Например 11 12 13 12 2 10 9 23 33 а н т и с и м- 0., взаимный данного симметрического, сам симметрический. Если aij = - и следовательно /j- = О, то О. ш.зыгается косым симметрическим, или метрическим. Например О 12 13 - 12 О 23 - 13 - 23 О Легко проверить, что косой симметрический О. нечетного порядка равен нулю. В тензорном исчислении пользуются аналогичными терминами-симметрич. и аитисимметрич. тензоров. Пользуясь теоремой сложения О., можно любой тензор раз.тожить на два тензора - симметрический и антпсимметричес-кий. В прилож ПИЯХ встречаютсяCiiMM трич. О., вычислергае к-рых сводится к вычислению т. н. циклпч. О. Симметрич. О. вида 1 а 2 3 n . 1 ,., 1 называется циклическим О., или циркулянтом. Обозначая корень п-й степени из единицы через I аг--- а 3... 1 (n-l)(n-2)n-l = (-1) 2 П( 1 + п 1 - и-1 + асо* -Ь а^о} -Ь ... -Ь co( -i)*). Определитель
В к-ром сумма квадратов элементов в каждой горизонтали равна единице, а сумма произведений соответственных элементов двух каких-либо горизонталей равна нулю, т. е. в к-ром li+ !2 + -. + ! = !, el /l + 2 i2 + + № iM = О (г i), называется ортогональным. Например при повороте прямоугольных координатных осей вокруг начала координат ф-лами преобразования будут Xi = 1Ж + bi?/ +Ci, 2/1 = аЖ + Ъ^у -cz, Zi = 3Ж -f by +CsZ, где a; Ь/ Ш Ci (i = l, 2, 3) - направляющие косинусы. О. этой системы 1 с>1 Ci 2 2 2 3 Ьз Сз будет ортогональным, потому что, как известно, будут существовать соотношения: ?+Ь!+с? = 1, 1+Ь|+с| = 1, 1 2 + bibg -Ь С1С2 = о, ajflg + bibg + С1С3 = О, 2 3 + 23 + С2С3 = 0. Если в ортогональном О. переставить вертикали и горизонтали, то преобразованный О. опять будет ортогональным. Произведение двух ортогональных О. является также ортогональным О. Возведя ортогональный О. D в квадрат, получим 1)2 = 1, откуда D=±l, т. е. числовое значение всякого ортогонального О. равно единице (Якоби). Рассмотрим т. н. функциональные О., в к-рых элементами являются ф-ии одного или нескольких переменных. Если элементы О. D являются независимыми переменными, то из тождества D = а/1 + ttiAi + ... + ttinAin следует Если же элементы О. D являются ф-иямиж, то dx ~ 4г^дщк' с1х ~ Хигк эс обозначая через а', имеем при п = 3: dD dx или 11 12 13 21 22 23 31 32 33 11 12 13 21 22 23 31 32 33 11 12 13 21 22 23 31 32 33 а dull d i2 dttis 21 22 23 32 33 11 + I 21 da.. 12 22 11 12 13 d 2i 22 23 31 ЯЙ Я 13 23 rf S3 Вычислим т. наз. степенной О., или определитель Варщермонда: 1 ...1 rf.n-1 грП-1 rp>. >1 tJU . t*,; O. V является целой однородной функцией ~-ой степени переменных Ж1, ж , ж^. Так как замена переменного ж„ переменным жДа, р= 1,2, ...,п; аф) обращает О. V в нуль, то делителем О. V будет произведение П(ж„ -Жд), распространенное на всевозможные значения для а и /5, причем будем считать а> . Число множителей вида ж„ - ж^ будет Сп, т. е. степень делителя будет та же, что и у ф-ии V. Следовательно возможно следующее равенство: F = АП(Жа -Хр), где Д-численный множитель. Из сравнения какого-либо члена О. F с таким же членом делите.пя следует, что 1=1. Итак: 1 1 ...1 .ж^ .х1 = 11(Ж„-Ж^), ,i8 (15) где а, /5 = 1,2, W и а > Если в О. (15) Ж1, Жз,Хп-корни ур-ия /(ж)=0, то квадрат О. V называется дискриминантом (см.) ур-ия. И^еем: 1 1 ... 1 Xi Ж2 . . Ж^ х\ ж! ... Ж)1 F2 = = П(Ж„-Ж.)2. Дискриминант есть симметрич. ф-ия корней ур-ия и поэтому м. б. BbipajKCH рационально через коэфициеты ур-ия /(ж)=0. Обращение дискриминанта в нуль является необходи-мьш и достаточным условием существования кратных корней ур-ия. Возвышая V в квадрат по правилу перемножения О. и введя х\ + х\+ ...+x>l = 8k, получаем выражение для дискриминанта: Si S2 .. .Sfi 72 = в K-poM суммы одинаковых степеней корней вычисляются по известным ф-лам Ньютона. Определитель А /2 ... fn (16) (п-1у(п-1), д -1) в к-ром fl, /2,/ -ф-ии переменного ж, называется определителем Вронского. Взяв мы увидим, что изменится только порядок производных в последней горизонтали- повысится на единицу. Приведем еще такое свойство определителя Вронского: Wih, A/j, А/ ) = Я . ЩД, f ...,/ ), (17) 1 2 3 4 5 6 7 8 ... 49 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© 2007 SALROS.RU
ПромСтройМат |