• Что такое фактурная штукатурка
• Выбираем сухие строительные смеси
• Преимущества напряженного железобетона
• Что влияет на выбор кровельного материала
• В чем преимущество пробковых полов

Схема о. мокрым способом приведена выше (фиг. 1); слева показано удаление воды фильтрпреесами, справа-осмосмашинами, а применяемые аппараты по стадиям-ниже.

Каолин-сыреп i

Дробление

Электролиты

(дробилки, вращгчющнйся барабан, мешалка)

Выпадение крупного песка (песочные ящики, машины Эксцельсиор и Бавария , классификатор Дорра) 4-

Выпадение мелкого песка и ш.л1офа (ящики 2-го ряда, лабиринты, клас-сифтааторы Дорра с чашей) 4-

Бассейны <-

(отстойные и для коагуляции) 4,

Удаление излишней влаги: [а) филътрпрессы, вакуум-фильтры, электроосмосмашины, б) сушилки]

Склад

В последние годы при О. начали применять в производственном масштабе электролиты: NaOH, растворимое стекло, защитные коллоиды органич. происхождения. Каолин-сы-

Фиг. 2.

рец в кусках или в виде экскават-струяеки подается во враш;а10щийся барабан (обычно с диам. 1-1,5 м, длиной 3-4 м), внутренняя поверхность к-рого усажена металлич.

происходит в разбавленных суспензиях при плотностях не выше 5-9° Вё во избежание нарастания вязкости, препятствующей выпадению крупньпс частиц. Добавление электролитов в известных концентрациях способствует пептизации глины и устойчивости суспензии. При этом плотность суспензии м. б, доведена до 20-30° Вё, причем более-крупные примеси легко вьшадают вследствие уменьшения вязкости. При дальнейшем прохождении суспензии выпадают более мелкие частицы примесей.

Типы машин, в которых происходит улавливание песка и других механич. примесей следующие. 1) Система песочных ящиков, в которых на дне осаждается песок, а суспензия поверху переходит из одного ящика в другой. Вьгаадение песка из суспензии воз-момсно, когда скорость падения частиц песка больше скорости подъема суспензии в ящиках. Для окончательного выпадения мелких примесей при.мепяют в некоторых случаях лабиринты (длинные жстоба). Скорость движения суспензии необходимо выбирать оптимальную. При быстром потоке возможен унос более крупных частиц; при слишком медленном-потери осаждающегося в ящиках и желобах каолина. Выбираемая плотность суспензии должна обеспечивать максимальное вьшадение песка и минимальную, потерю каолина. Применение конич. ящиков способствует наилучшему О. 2) Отмучи-ватедьная машина (фиг. 2) представляет собой систему вращающихся цилиндрических сит и колес с ковшами, находящихся в чане, в к-ром материал поступает с одного конца, а вода идет навстречу. Выпадающий из суспензии песок различной крупности удаляется черпачными колесами. 3) Кпассификато-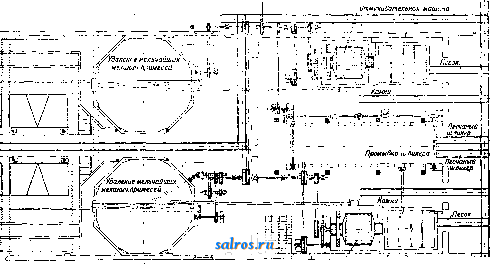

/ Отмуяибатемьная ыашииа

Флг. 3.

ножами или пальцами, облегчающими разбивание кусков при вращении, или в мешалку, имеющую один или два вращающихся вала с насаженными на них ножами. Из мешалки или барабана каолпн выходит в виде суспензии; крупные зерна примесей быстро выпадают в песочных ящиках. Вьшадение

ры типа Дорра с чашей начинают применять в США и в Германии. Суспензия поступает в классификатор в середине чаши; крупные примеси оседают на дно и через отверстие удаляются скребками. По Анаблю-классификатор с чашей для очистки каолина из Сев. Каролины обрабатывает 3 m в час и

дает продукт, 95-98% которого проходит через сито с 16 ООО отверстий на см при потреблении 2 БР и значительном снижении рабочей силы. Опыты Механобра показали часовую производительность чаши диам. 1 м в 61 кг сухого каолина, причем остаток на сите в 10 ООО отверстий не превышал 0,5% (Н. Кочкин). План расположения аппаратуры отмучивательного отделения каолиновых заводов показан на фиг. е,. 4) О. при иомоищ центрифуг не вышли пока за пределы лабораторных опытов. По Бауеру центрифуга диам. 20 см, делающая 50 об/ск., в 1 ООО раз увеличивает скорость отделения по сравнению с осаждением иод влиянием собственного веса.

Следующей стадией является удаление излишней влаги из каолина. В специальных чанах каолин отстаивается в течение 5-1 дней, осветленная вода удаляется с поверхности. Благодаря прибавлению электролитов (AlCls, CaCla, Са(0Н)2, H2SO4, НС1 и др.) происходит немедленная коагуляция каолина, что оказьшает положительное влияние на скорость фильтрования и делает излишними отстойные бассейны. Удаление воды происходит при помощи фильтрпрессов периодич. действия с рамами под давлешхем 8-10 atm. Влажность получаемых коржей 28-32%. Применение вакуум-фильтров (см.) в каолиновом деле находится в стадии опыгов. Разрешение проблемы должно ИТТИ в плоскости снижения расхода энергии и уменьшения влажности. Другим видом установок для удаления влаги служит элект-роосмотич. машина (фиг. 4). Глинистая муть подаетс^{ по трубе а в корытообразные сосуды б и бх с мешалками в; далее муть проходит через сетчатый электрод г и входит в соприкосновение с вращ,ающим-ся (20об/мин.) свинцовым электродом д. . Осадок вращением -анода поднимается и с помощью скребка е Снимается в виде массы с влажностью 25- 35%. Применяют постоянный электрич. ток напряжением около 100 вольт при плотности тока на аноде 0,01 А/см. Расход электрич. энергии на каолиновом заводе в Шодау на 1 т сухой глины 87,5 kWh. Заводские установки этих машин в Германии и других странах пока не привились по экономическим соображениям. Для более пластичных глин могут найти применение электроосмотические фильтрпрессы, рамы которых представляют собой электроды. Для доведения каолина до продажной влажности (10-12%) требуется его высушить в сушилках. Применяются сушилки камерные, канальные, барабанные. Каолин сушится паром или горячим воздухом при t° 80-120°. Есть предложения обходиться без калориферов путем нагревания каолина непосредственно смешанньиии с воздухом горючими газами, полученными от сжигания нефти или кокса.

Лит.: Лысин Б. и Га.т1абутская Е., Материалы к изучению каолинов Украины, Киев, 1929; .Яучицкий в. И., Каолины Украины, Труды Института прикладной минералогии , Москва, 1928,

Фиг. 4.

вьш. 41; Г е л ь д Н., О способе обогащения каолинов и глин. Материалы по обогащению полезных ископаемых, Труды Института механической обработки полезных ископаемых , Д., 1928, вып. 1; его же. Связь между устойчивостью каолиновых и глиняных суспензий и Ph, там же, 1929, вып. 2; Гел ьд Н. и Корнилов Д., Исследование о влиянии различных факторов на скорость фильтрования каолинов и глин, отмученных на растворах жидкого стеь--ла, там же; Stark J., Die physikal.-technlsche Un-tersuchung keramischer Kaoline, Lpz., 1922; R 1 e к e R., Schlammgeschwlndigkeit u. Korngrosse, eBerichtc d. deutschen keramischen Gesellschaft*, В., 1927, 8; Bauer E., Die Methoden zur Bestimmung d. Korn-grossen von Kaolinen u.Sonen,ibid;, 1924, 5; L a u Ь e n-helmer A., Der Kaolinbergbau im nordwestsachsi-schen Porphyrgebiet, Berichte d. deutschen keramischen Gesellschaft , Berlin, 1930, 4; Sproat J. E., Refining a. Utilisation of Georgia Kaolins, Bureau (f Mines*, Wsh., 1916, Bui. 128; Shurecht H. G., The Use of Electrolytes In the Purification a. Preparation of Clays, Bureau of Mines , Technical Papers, Wsh., 1922, Bui. 281; A n a b 1 e A., Dorr Classifiers fcr Clay Washing, Journ. of the American Ceramic Soeiety , Columbus, Ohio, 1928, 2. И. Ииинкельштейн.

ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ. Совокупность физич. теорий или положений, объединяемых термином теория относительности , иногда принцип относительности , в процессе исторического развития физики меняла свое содержание как по объему, так и по качеству. В так наз. классич. механике, к-рая до появления в 1905 г. новых теорий Эйнштейна считалась единственно возможной и безусловно доказанной на опыте, под относительностью, или законом относительного движения (слово теория в сочетании с термином относительность еще не применялось), понимали независимость основных ур-ий механики от равноноступательного движения координатной системы, к которой они отнесены, по отношению к нек-рой другой основной координатной системе, так или иначе связанной со всей совокупностью имеющейся в мире материи, например с ее центром тяжести или же, как у Ньютона, с нек-рым абсолютным пространством. В современной терминологии такая относительность формулируется след. обр.: ур-ия движения механики тд = f, где т-масса, д-вектор ускорения, /-сила, приложенная к т,кова-риантны к преобразованию координат (см. Тензорное исчисление):

х' = х + vj: у' = у + Vyt; z = z + vj; (1) причем масса m считается скаляром, силы же преобразуются по правилу

В ф-лах преобразования Vg., Vy, Vg означают компоненты скорости, a t-время, одинаковое в обеих кооодинатньис системах, т. е.

V=t. (3)

В классич. трактатах по механике и физике указывается обычно только положение (1); необходимость добавления в явной форме положения (2) и (3), утверждение об инвариантности массы, а также и экспериментальное содержание этих положений выясняются лишь после возникновения новых теорий Эйнштейна. Эта относительность имеет в настоящее время в физике название принципа относительности Галилея-Ньютона.

Специальная О. т. Безусловная применимость этого принципа ко всем явлениям, считавшимся в 19 в. чисто механическими, за-

ставляла физиков этого века искать подтверждения или опровержения его на других явлениях, с точки зрения того времени-не чисто или вовсе не механических, напр. оптических, электрических и т. п., но к-рые можно было бы пытаться объяснить и механически. 19 век создает теорию эфира, сначала упругого (Френель, Нейман), затем электромагнитного (Фарадей, Максвелл, Герц, Лоренц и др.). В различных теориях эфир по-разному связан с материей. Теории Лоренца и Герца представляют в этом отношении две взаимно исключающие крайности. По Лоренцу эфир свободно проникает материю. Материя в движении совсем ни в какой мере не увлекает за собой эфира. Эфир, не участвующий в движении материи, естественно связывается с тем абсолютным пространством, по отношению к которому прямолинейное и равномерное движение не меняет законов чисто механич. явлений. Но теория Лоренца приходит к выводу, что принцип относительности Галилея-Ньютона к явлениям оптическим или электромагнитным не применим. Поэтому соответствующим оптич.или электрич. опытом можно было бы пытаться обнаружить поступательное равномерное движение относительно эфира. Образцом такого опыта является знаменитый опыт Майкельсона. Он состоит в следующем: интерферометр (см.) Майкельсона устанавливается так, чтобы направление SP совпало с направлением движения земли в ее вращении вокруг солнца; при этом наблюдатель видит нек-рую интерференционную картину. Затем весь прибор поворачивается на 90°, так что с направлением движения земли совпадает линия MQ. С точки зрения классич. теории должно произойти смещение полос интерференции, равное

где I - длина плеча интерферометра SP, предполагаемая равной MQ, Я-длина световой волны, V-скорость земли относительно эфира, с-скорость света и d-расстояние между 2 полосами интерференции. Ожидаемое смещение достаточно велико для того, чтобы его можно было наблюдать. Как первые наблюдения Майкельсона (1888 г.), так и сравнительно более поздние его повторения (1926 г.) привели к выводу, что ожидаемого смещения полос не наблюдается. Теория Герца, наоборот, связывает материю с эфиром. Эфир полностью участвует в движении материи. Вследствие этого оптическими или электрическими экспериментами, производимыми внутри движущегося тела, движения его относительно других тел обнаружить нельзя; принщш Галилея-Ньютона должен быть справедлив.

На примере этих двух теорий видно, что принцип относительности по содержанию всему должен иметь для всей физики весьма большое значение. В этом обстоятельстве кроется причина, почему именно электродинамика движущихся тел и привела в 1905 г. к созданию т. н. специальной теории отно-сительности, заменяющей классич. принцип Галилея-Ньютона. Теория Герца в нек-рых своих выводах согласна с опытом (напр. вышеупомянутый опыт Майкельсона), в других

т. Э. т. XV.

резко ему противоречит. Электронная теория Лоренца лучше согласуется с опытом, все же она в своем первоначальном виде не всегда оказывается правильной (тот же опыт Майкельсона). С добавлением гипотезы (гипотеза Лоренца и Фицджеральда) о сокращении размеров тел по направлению движения в отношении /1 - , где v - скорость

тела и с-скорость света, теория Лоренца объясняла для движущихся тел все опыты, известные к началу нашего столетия. Весьма важно отметить, что теория Лоренца вместе с гипотезой о сокращении тел по направлению движения привела к ряду выводов, вызвавших переоценку основных положений классич. механики. Мы отметим из них следующие. 1) Электромагнитный эфир как основа для абсолютной координатной системы оказывается неуловимым при расчетах электромагнитных явлений; им нужно пользоваться, но вследствие сокращения тел по направлению движения всякая экспериментальная попытка обнаружить его заранее обречена на неудачу. 2) В двух системах К к К', двигающихся относительно эфира прямолинейно и равномерно, но с различными скоростями, соотношения между электрич. силами Е и Е' я магнитными Н и Jf вовсе не определены выражениями (2), а более сложными; если движение К' относительно К параллельно оси X и относительная скорость движения будет Vr, то для электрич. силы например имеем:

г; = Е^; ЕуЕу-\ vHi, Е', = Е, + vHy.

3) Весьма удобным при расчетах электромагнитных явлений в координатной системе, двигающейся относительно эфира со скоростью Vx, оказывается введение вместо абсолютного времени t времени += t, где

X-абсцисса; время f, разное в различных местах пространства, Лоренц назвал местным временем. 4) Поток лучистой энергии может быть рассматриваем как количество движения и при расчетах движения излучающих или поглощающих лучистую энергию тел должен быть принят в соображение рядом с обыкновенным механическим количеством движения.

Эйнштейну удалось показать, что эти выводы теории Лоренца можно облечь в значительно более простую и понятную форму, если пересмотреть классич. представления физиков о времени и пространстве. Измеренная длина тела, измеренный промежуток времени или установление момента одновременности в различных местах пространства получаются в физике как результат физич. манипуляций над вещественными телами. Основным и неизбежным посредником для установления одновременности двух событий является свет, и физич. понятие об одновременности становится определенным только при допущении, что скорость света д. б. величиной постоянной во всех движущихся прямолинейно и равномерно друг относительно друга координатных системах; эта скорость для материи д. б. предельной скоростью; при переходе от одной системы К к другой К' ф-лы преобразования (1) и ( 3) д. б.

заменены следующими (если предположить для. упрощения скорость движения совпадающей по направлению с осью X, что существенного значения не имеет):

У^у: 2= ,2; (Г)

V2 С2

Ни длина Al = X2 - Xi mi промежуток времени At= к - к не являются в силу физич. приемов их измерения инвариантами, не зависящими от избранной системы координат. Инвариантом будет их сочетание: М^ - cAi, к-рое можно обозначить через AS или -Лт в зависимости от того, будет ли AlycAt или Al<cAt. Физическое различие между временем и пространством сохраняется при всем этом вполне. Формула сложения двух одинаково направленных скоростей и v, вытекающая из преобразований (1) и (3), примет следующий вид:

где V-результирующая скорость, в отличие от соответствующей ф-.чы классич. механики V = Vi + v. Как легко проверить, эта ф-ла соответствует существованию предельного значения скорости света с.

Формулы (1) и (3), известные под именем ф-л преобразования Лоренца, являются выражением новой относительности Эйнштейна. При скоростях, малых по сравнению со скоростью света, эти ф-лы практически совпадают с (1) и (3); они объясняют т. н. сокращение тел по направлению движения и удобство применения местного времени как результат физич. приемов измерения длины и времени. Т. к. существование предельного значения скорости света с и ф-лы (1) и (3) не соответствуют классич.механике, то требуется пересмотр основных ее положений вообще и вместе с тем, в частности, пересмотр ф-лы преобразования сил (2). Поэтому содержанием О. т. теперь уже является не только относительность движения, но и новые динамика и теория электричества.

Отметим нек-рые положения новой динамики. 1) Вместо ур-ий Ньютона имеем для материальной точки:

где q-скорость движения материальной точки, а то-скалярная величина-масса покоящейся точки. Вместо закона живой силы классич. механики имеем:

mocs

= Fq.

Следует заметить, что силы F не удовлетворяют положению о иреобразовании их (2). Если вектор / означает силу F, отнесенную к единице объема, то преобразование сил при переходе от одной координатной системы К

к другой К' рассчитывается для / по ф-лам:

fx + vlt

/; = /.

при

2) Если рассматривать вектор G =

как количество движения, то коэф. при скорости q можно рассматривать как массу т.

Эта масса m = -зависит от скорости..

Если в опытах при расчетах движения пользоваться классич. ф-лой mq = F, то величина т должна оказаться при достаточно больших скоростях зависимой от скорости q, что и подтверждается опытом. 3) Выражение для кинетич.энергии классической механик

есть только первое приближение для

нее; более точное ее выражение имеем в (6). 4) С формальной стороны выкладка очень-упрощается, если рассматривать ж = ccj; = ?/i;. z = Zi; ctXi как координаты нек-рого четырехмерного многообразия, а физич. величины, определяющие электромагнитное состояние вещества, как компоненты соответствующих тензоров соответствующих рангов четырехмерного многообразия. Теория электромагнитных явлений и динамика О. т. в такой форме впервые была изложена немецким математиком Минковским (1907 г.).

По отношению к теории электромагнитных явлений можно заметить следующие положения. 1) Векторы .Ё и Л рассматриваются как кососимметричные компоненты тензора второго ранга в четырехмерном многообразии с^ координатами х^, х^, Xg, х^. Преобразование-их на основании соответствующих теорем тензорного исчисления при переходе от одной координатной системы к другой по преобразованиям Лоренца поэтому будет:

Е' = Е,; E: = (E,-Iv,H,)

E = {E, + \v,Hy)

что согласно с выводами теории Лоренца к-рая в ф-лах преобразования для этих тензоров отбрасывает члены, содержащие квадраты отношения 2) Максвелловские напряжения вместе с потоком лучистой энергии и плотностью энергии электромагнитного ноля объединяются в общий тензор второго ранга, получающий название тензора, максвелловских напряжений и энергии. Расхождение этого тензора дает силы, действующие на заряды в покое или движении. Преобразование этого тензора при переходе от К к К' показывает, что энергия может выступить в роли массы. Таким образом О. т. строго оформляет принцип эквивалентностш

массы и энергии. Во всех своих выводах специальная О. т. находится в согласии с наблюдением. Из наиболее замечательных экспериментов, послуживших к ее обоснованию и утверждению в физике, следует отнести: 1) опыт Майкельсона; 2) опыты для

определения , т. е. отношения заряда электрона к его массе при больших скоростях; 3) тонкую структуру спектральн. линий [i].

Общая 0. т. Вьппе мы видели, что если ур-ия механики и электромагнитного поля верны в нек-рой системе отсчета К, то они же верны и во всякой другой системе К', движущейся относительно К равномерно и прямолинейно. Но если iC движется относительно К с ускорением, то законы механики получат в системе К' более сложньш вид: это усложнение можно описать, введя особого рода инерциальные силы (центробежную силу, силуКориолиса), к-рые с точки зрения наблюдателя К' сообщают всем телам ускорение, не зависящее от массы этих тел. Может казаться, что наличие инерциальных сил убедит наблюдателя К' в том, что его система отсчета движется, но это неверно. Известно, что не только инерциальные силы, но и сила тяжести обладают тем свойством, что влияние их на движение тел не зависит от массы этих тел (ср. опыты Галилея над падением тел); поэтому наблюдатель К' может считать свою систему отсчета неподвижной, а вместо инерциальных сил ввести особое поле тяжести, производящее такие же самые действия. В 1916 г. Эйнштейн облек этот вывод в форму принципа, гласящего: каждая система отсчета с таким же правом может считаться неподвижной, как и любая другая; все системы отсчета равноправны; все законы природы можно сформулировать так. обр., чтобы одна и та же формулировка была действительной для всех возможных систем отсчета. Это требование ковариантности получило название общего принципа относительности; его содержание шире, чем содержание специального принципа, в к-ром речь идет лишь об инерциальных системах отсчета.

На этом принципе Эйнштейн построил новую теорию пространства и времени. Ее содержание таково: пусть наблюдатель К установил координатную систему, в к-рой каждая пространственно-временная точка ( событие ) характеризуется четырьмя координатами Хх, Xs, Жз, Ж4. Два близких друг к другу события с координатами х^, Жа, х^, х^ и х^-}-dxi, Х2 4- dXif 3 + dx, Х4, + dXi определяют интервал или длинр>

QidXidxy,

где Qik-нек-рые ф-ии координат х^, х^, х^, Ж4 (причем дгк^Отсг)- Мы будем писать сокращенно:

ds = VgikdXidx, (8)

следуя правилу суммирования : если какой-Ш1будь значок повторяется в каком-либо одночлене дважды, то по нему производится суммирование от 1 до 4, хотя знак S для

краткости опускается (например а^Ъг значит

aibi. Интервал есть инвариант; это зна-

г = 1

чит, что при переходе к другой координатной системе х\, х', х'з, xi мы должны подобрать в ней функции fifj-jc так, чтобы было

gik dxi dx = gfi dXi dx. Ф-ИИ gfjfc определяют геометрию четырехмерной протяженности ( пространства-времени ); если два события являются с точки зрения К одновременными, то интервал между ними определяет результат измерения их пространственного расстояния друг от друга в системе отсчета К; если же оба события произошли в одном и том же месте пространства (с точки зрения К), то интервал между ними определяет время, протекшее между обоими событиями и измеренное по часам системы отсчета К. Так, функции Qik управляют поведением часов и. материальных масштабов. Они же управляют и движением тел: всякое тело, на к-рое не действуют электромагнитные силы, движется так, что его четырехмерная траектория является геодезич. линией e/ds = 0; диференци-альные ур-ия такой линии

dji X {hl\dxhdxi .

ds2 1 г / ds ds2 >

символом I } (символ Христоффеля) сокращенно обозначается сумма

1 j)igg (дщи , &дц ()9ki\

2 dgij \дх1 ~ dxfc dxj}

где д есть определитель Igrjt!. Лучи света также удовлетворяют этому ур-ию, но для них кроме того д. б. ds=0.

Если геометрия рассматриваемой четырехмерной области такова, что она доп^скает введение координатной системы х, у, z, t, в к-рой ds принимает вид

ds =-dx- dy-dz -f c4t, (10)

TO все символы Христоффеля в такой системе обратятся в нуль, и из ур-ия геодезич. линий будет следовать, что х, у, z-линейные ф-ии t. Поэтому в такой системе отсчета все тела, на к-рые не действуют электромагнитные силы, движутся прямолинейно и равномерно; свет распространяется по прямым линиям со скоростью с. Условия, с к-рыми физик имеет дело в действительности, всегда таковы, что ф-ла (10) в первом приближении может считаться верной. Если же геометрия рассматриваемой области пространства-времени не позволяет ввести систему отсчета, в к-рой имеет место ф-ла (10), то тела, на к-рые не дрйствуют электромагнитные силы, будут двигаться с ускорением, какую бы систему отсчета ни вводить, причем это ускорение не зависит от массы тела. Выражаясь обычным языком, мы сказали бы, что в рассматриваемой области пространства-времени действуют силы тяготения, но О. т. обходится без введения специальных сил : в искривлении траектории тела она видит лишь результат такой геометрии пространства-времени , в к-рой обычные ур-ия прямой уже не дают геодезич. линии (неэвклидова геометрия); напр. планета описывает вокруг солнца эллипс не потому, что солнце ее притягивает , а потому что солнце производит

местное искривление пространства-времени , благодаря которому четырехмерная гео-дезич. линия соответствует движению планеты не по прямой, а по эллипсу.

Опыт показывает, что поле тяготения связано с присутствием материальных тел; закон, но которому геометрия четырехмерного пространства-времени связана с присутствием материи, принято называть законом тяготения . В поисках надлежащей формы этого закона Эйнштейн должен был удовлетворить требованию ковариантности и кроме того дать такую теорию, в к-рой теория Ньютона содержалась бы как первое приближение. Найденный им закон тяготения гласит (и-постоянная величина):

Giu-->{Tik-\gikT), (И)

где Gгl, = щ{] + {{] {1) (сокращенный тензор Римана) и где Т^-так называемый тензор материи. С^л = (?о' бо-плотность материи, - ее четырехмерный вектор скорости; Т =-- у: Т^; впоследствии к тензору Тд. были прибавлены члены, зависящие от присутствия лучистой энергии.) Кроме того можно показать, что при малых скор)ОСтях материи (по сравнению со скоростью с) ур-ия геодезич. линии (9) дают

а ур-ия поля дают

/92 в2 Э2 \

т. о. 2 041 играет роль ньютонова потенциала и мы получим обычное ур-ие Пуассона, если полояим

,i = s= 1,87.10- ,

где К-постоянная тяготения.

Эйнштейн,Шварцшильди Дросте применили ур-ия (9) и (11) к движению планет в поле тяжести солнца. На расстоянии г от солнца геометрия пространства-времени определяется ф-лой

- r\d -Ь sin2 & d<p), (12)

где m-постоянная, представляющая массу солнца, измеренную в особых единицах. При этом Gik = 0, и только при г=0 ур-ия имеют особую точку. Ур-ия (9) в первом приближении дают движение планеты по законам Кеплера, на к-рое накладывается вековое перемещение перигелия, достигающее заметной величины лишь у ближайшей к солнцу планеты, Меркурия f]. М. Бронштейн и в. Фредерике.

Кроме векового перемещения .перигелия Меркурия в 42,9 О.т. предсказывает искри-влерие лучей, проходящих вблизи поверхности солнца (1,75 ), и смещение спектральных линий в красной части спектра, причем соответствующее уменьшение частоты колебаний составляет для солнца 2,13-10-. Все эти величины лежат в пределах возможности измерения средствами современной астрономии, что открывает три различных пути к проверке О. т. Непосредственные наблюдения дают,

как это было найдено Леверрье, для перемещения перигелия Меркурия 565 в столетие. После учета взаимных притяжений планет путем координации надлежащим образом их масс, элементов их орбит, движения равноденственной точки по отношению к системе ярких звезд и многочисленных астрономич. постоянных для движения перигелия получилось всего 527 . Разница в 38 осталась необъясненной. Более обширное исследование Ньюкомба показало,что разность между наблюденным и вычисленным движением перигелия Меркурия доходит до 42,6 и значительно превышает погрешности наблюдения. Принимая во внимание позднейшую поправку Ньюкомба для движения равноденственной точки,эту разность приходится увеличить до 45,9 . Обработка многочисленных рядов позднейших наблюдений, произведенных до 1925 г., показала необходимость введения дальнейших поправок, именно 5,0 в столетие, вследствие чего необъяс-ненное движение перигелия Меркурия нужно в настоящее время считать в 50,9 . Этот результат не является вполне точным. Небольшие неправильности в планетных массах, возможное сжатие солнца, обнаруженное недавно вращение звездной системы, по отношению к к-рой определяются координатные оси, и ряд других причин могут изменить указанную величину на несколько ск. дуги. Это неравенство не является к тому же единственным в солнечной системе. Вековое изменение долготы узла орбиты Венеры, дви-нсение перигелия Марса и т. п. равным образом не м. б. полностью объяснены лишь взаимным притяжением планет. Остаточные неравенства в этих случаях далеко превосходят погрешности наблюдений. О. т. дает указанное выше перемещение перигелия Меркурия в 45,9 в. сто летне в предположении, что эта планета не подвержена действиям посторонних возмущающих сил. Остаточные неравенства других планет, для к-рых О. т. дает совершенно ничтожные величины, остаются без всякого объяснения. Выводы О. т. не находятся в противоречии с данными наблюдений, но во всяком случае преждевременно говорить об ее подтверждении на основе данных позиционной астрономии.

Не лучше обстоит дело с проверкой О. т. на основании отклонения светового луча в силовом поле солнца. На возможность подобной проверки путем наблюдений звезд около края солнечного диска во время полных солнечных затмений было указано в 1914 г. Специальные экспедиции были организованы в 1919 и 1922 гг. в Бразилию и Австралию. Для возможности нахонсдения искомых весьма малых смещений звезд по радиальному направлению от края солнечн. диска принято тем же инструментом фотографировать Область неба, в к-рой находилось солнце во время затмения, но по необходимости в другое время года и других °-ных условиях. -Одинаковость масштабов обоих снимков определяется из условия, что наиболее удаленные от солнца звезды, вышедшие на пластинке, не имеют никакого радиального смещения. В этом предположении для ближайших звезд получаются радиальные смещения, в общем соответствующие эффекту

Эйнштейна для данного расстояния от края диска. Однако различия между отдельными определениями весьма велики и искомое смещение получается в результате значительной экстраполяции. Тангенциальные смещения звезд, по величине сравнимые с радиальными и имеющие явно выраженный систематич. характер, обычно рассматриваются как случайные погрешности. Из общего числа звезд, полученных 1-й экспедицией, было использовано всего 15% для проверки О. т., а второй-50%. Звезды с весьма большим смещением, в особенности направленным к солнцу, а не от него, не вошли в рассмотрение. Полученные результаты, при выводе к-рых заранее предполагалось, что эффект Эйнштейна является единственной npi-шиной радиальных смещений, не являются поэтому вполне доказательными, тем более, что они м. б. объяснены и другими причинами, напр. т. н. космич. рефракцией Курвуазье.

Третий путь для проверки О. т.-смещение спектральных линий к красной части спектра представляет лучшие возможности. Предсказанная величина для солнечной поверхности, именно 2,13-10 в частоте колебаний, легко м. б. измерена современными средствами, погрешность к-рых не превышает примерно 3-10~. Действительно, почти все линии спектра показьшают смещение в ожидаемом смысле. Однако вопрос чрезвычайно усложняется тем обстоятельством, что величина этих смещений крайне различна для разных линий и вообще увеличивается с их интенсивностью. Согласно С. Джону этот эффект м.б. объяснен тем, что наиболее интенсивные линии, берущие свое начало на больших высотах над' солнечной поверхностью, принадлежат слоям, систематически опускающимся вниз, в результате чего предполагаемый эффект Эйнштейна увеличивается реальным допплеровским смещением. Слабые линии принадлежат повидимому к более низким слоям. Малые смещения этих линий к красной части спектра можно объяснить предположением о восходящих токах в этих слоях, уменьшающих эффект Эйнштейна. При этом делается однако произвольное допущение, что на уровне, соответствующем линиям с интенсивностью 6-8 по шкале Роу-ланда, никакого вертикального перемещения вещества нет. Интерпретация С. Джона встречается кроме того с тем затруднением, что относительное смещение линий различной интенсивности не зависит от положения по отношению к центру солнечного диска, как это было установлено Меггерсом и Берн-сом. Более надежное средство для проверки О. т. тем же путем представляют т. н. белые карлик и-звезды с плотностями, в десятки тысяч раз превосходящими плотность воды, и соответственно большими значениями гравитационного потенциала. Для одиночных звезд этого рода эффект Эйнштейна неотделим от обычного допплеровского смещения и потому не м. б. обнарулген. Только если подобная, звезда является спутником другой, с уже известной радиальной скоростью и известным расстоянием их от наблюдателя, если кроме того массы этих звезд известны, а объемы их выведены, например путем сравнения абсолютной яркости с со-

ответствующей t° поверхности, имеются все предпосылки для вычисления эффекта Эйнштейна на поверхности белого карлика и сравнения его с наблюдениями. Сочетание таких условий имеется пока только для спутника Сириуса. Наблюдаемое смещение соответствует 19 км/ск; предсказанное-17 км/ск. При выводе этого результата предполагалось, что яркость спутника Сириуса не зависит от присутствия на близком от него расстоянии главной звезды, превышающей его по яркости в 10 000 раз, и что по характеру спектра белого карлика, установленному к тому же не вполне точно, молшо судить об его Г. Позднейшее определение цветного показателя спутника Сириуса несколько увеличило расхождение между наблюдениями и теорией. Кроме того нужно указать, что аналогичные смещения линий к красной части спектра известны для различных звезд нашей звездной системы. Для звезд типа В в отдельных галактических долготах эти смещения доходят до 8 км/ск и совершенно не объясняются теорией относительности. Из всего изложенного выше следует, что О. т. в настоящее время не м. б. проверена совершенно несомненным образом при помощи астрономических наблюдений. Тем не менее ни одно из известных явлений ей не противоречит, в. Фесенков.

0. Т. И КОСМОЛОГИЯ, в 1917 г. Эйнштейн встретился с затруднениями при попытке сформулировать те условия, к-рым должно удовлетворять дц на бесконечном расстояний от материальных тел. Это заставило его перейти от прежней ф-лы (11) закона тяготения к более общей ф-ле

Огк - 9гк = - (Trt - I д,кТ), (13)

где А-постоянная величина. Преимущество ф-лы (13) над (11) заключается по мнению Эйнштейна в том, что ей может удовлетворять четырехмерный мир с конечным и замкнутым Б себе пространством, что делает формулировку упомянутых условий излишней. В связи с этим Эйнштейн поставил космологич. проблему: считая в первом приближении всю материю и лучистую энергию вселенной распределенными в ней равномерно, построить при этом условии такую геометрию четырехмерного мира, к-рая удовлетворяла бы уравнению (13). Решение, предложенное Эйнштейном, было таково:

-fcdi (14)

(цилиндрич. мир Эйнштейна), где R-посто^ янная величина, называемая радиусом мира,

и где для краткости написано х вместо .

При бесконечном R мероопределение (14) переходит в обычное мероопределение Минков-ского. Координаты х заключены между О я тг, (р мел-еду О и 2л, t между -оо и -Ь оо. Объем всего пространства = 2, масса

всей вселенной М= - Pi, причем на долю обыкновенной материи падает Мо = = остальное падает на долю излу-

чения. Наибольшая возможная масса иолу-

чится при = , ж = Жо = Д, причем

2Я 2А

плотность равна -. Если предположить =

= 2 10~ sJGM (такова приблизительно средняя плотность материи в пределах расстояний, доступных современным телескопам), то последние формулы дадут jR=2,3-10 см, М = Жо = 4,88 10 5 г; Я = 1,9 IQ-s слг-.

В. де Ситтер дал (1917 г.) другое решение той же космологич. проблемы, а именно:

ds- = - Щах^- -f x(d& + sin2 & d(p-2)] + -f c2 cos2 X dt (15)

(сферич. мир де Ситтера). Ур-ие (13) удовлетворяется при условии, что R = j/ и что

плотность и давление лучистой энергии равны нулю: мир де Ситтера пуст. Применять решение де Ситтера к реальному миру возможно лишь в том случае, если средняя плотность вещества во вселенной так мала, что ею можно пренебречь. Свойства такого мира весьма парадоксальны: все физич. процессы, происходящие на расстоянии от наблюдателя, представляются ему замедленными (благодаря наличию множителя cosх),

при % = , т. е. на расстоянии R, они представляются остановившимися. Если на некотором расстоянии от наблюдателя поместить тело малой массы, то, для того чтобы

удовлетворить принцину djds = О, оно должно двигаться; в некоторой определенной системе координат ( и Р, где P = Rtgx) его траектория - гипербола. Если с такого движущегося по инерции тела посылается световое колебание с длиной волны А, то наблюдатель в начале координат воспримет длину волны 2. -j- АХ, где в первом приближении

AA=A(±sinz + sm2 5j). (16)

Две причины изменения длины волны накладываются друг на друга: движение тела по гиперболе, к-рое может совершаться в том и в другом направлении, дает член ±sin;;c, пропорциональный расстоянию (астрономически измеренное расстояние есть R sin х), а замедление времени на расстоянии!? sin х от наблюдателя дает член sin;;, нропорцио-на.тьный квадрату расстояния.

Уже в 1917 г. было известно, что спектральные линии отдаленных звездных скоплений (т. н. спиральных туманностей) смещены преимущественно к красному концу (АЯ > 0), что де Ситтер объяснил наличием члена sinx изменяющего длину волны именно в этом направлении. В этом видели подтверждение ф-лы (15), хотя она, строго говоря, относится лишь к пустому миру, и опровержение ф-лы (14). В настоящее время (1930 г.) расстояния до многих спиральных туманностей измерены; при этом оказалось, что линии в их спектрах смещены почти всегда к красному концу. Красное смещение довольно хорошо удовлетворяет эмпирич. ф-ле

ДА = 5-10-28 Яг, (17)

гее г-расстояние в см. Т. о. эффект, пропорциональный расстоянию, имеет один и тот же знак, вопреки ф-ле (16), представляю-

щей следствие из (15). Поэтому в 1930 г. Эддингтон и де Ситтер для объяснения эмпирич. ф-лы (17) обратились к нестатическим решениям космологич. проблемы, разработанным в 1922 г. А. А. Фридманом (сконч. в 1925 г.) и в 1927 г. Лемэтром. В этих решениях ds пишется в виде (14), но радиус мира R C4irraeTCH не постоянной, а функцией вре- мени. Для объяснения ф-лы (17) нужно допустить, что он возрастает. Из теории Ле-мэтра вытекает, что

AA=-A(ig).r. (18)

Сравнение (18) с (17) дает

f(lgR) = l,5.10-\

т. е. при теперешней быстроте расширенпя мира он удваивается каждые 1,5-10 лет. Столь быстрое расширение мира (10® лет сравнимо с геологич. эпохами) весьма неправдоподобно и мало вяжется с теми сроками, какие нужны для эволюции звездной вселенной (напр. по Джинсу возраст нашей галактики 10 лет); поэтому следует признать полол^ение космологич. теории крайне неблагоприятным [*].

Единая теория поля. Геометрич. теория тяготения, созданная Эйнштейном, не претендует на раскрытие механизма гравитационных сил или их истинной природы; она дает лишь математич. теорию явлений, и роль геометрических представлений заключается только в том, что они позволяют сделать математику сравнительно простой и наглядной. Но у этой теории есть один важный недостаток: электромагнитным явлениям не нашлось места в ее геометрич. схеме; электромагнитное поле не получило геометрич. истолкования. Эйнштейн, Эддингтон и Вейль задались целью устранить этот недостаток и построить такую теорию, в которой электромагнитное поле, наравне с полем тяготения, является одним из геометрических свойств пространства. В этом и заключается проблема единой теории поля. Калуза (1921 г.), Клейн и Мандель (1926 г.) показа ли, что этой цели можно достигнуть при помощи пятимерной геометрии. Величина ds для пятимерного пространства получится, если к четырехмерной сумме Qik dXi dx}c прибавить

квадрат суммы Я^г^г, где <Pi, <р^, <Рз, i=l

обозначают электромагнитные потенциалы (т.е.= А^,= сfsl -г Р*=-9), а (р^-

постоянная величина. Ур-ия геодезич. линии в таком пятимерном пространстве дают дви-л^ение тела с зарядом е и массой т под влиянием электромагнитного поля (р^ и сил тяготения, определяемых через д^с- Максвелловские ур-ия электромагнитного поля и закон тяготения Эйнштейна могут быть представлены в виде инвариантных соотношений пятимерной геометрии. Никаких новых результатов при этом не получается; объединение электромагнетизма и гравитации в единую геометрическую схему происходит лишь формально. Поэтому, руководясь идеей'о том, что между тяготением и электричеством существует более интимная связь, Эйнштейн

продолжает искать построения единой теории поля в рамках четырехмерной геометрии. Обычная геометрия Римана оказывается для этого недостаточной; поэтому уже в 1918 г. Вейль предложил новую геометрию, содержащую больше независимых величин, чем геометрия Римана, и потому дающую воз-лиожность истолковать геометрически не только гравитационное, но и электромагнитное поле. В физич. теории Эйнштейна, основанной на геометрии Римана, длина бесконечно малого материального отрезка была инвариантной величиной; она имела всегда определенное значение, что давало возможность сравнивать длину двух бесконечно малых отрезков, расположенных в различных точках пространства (напр. в J. ив В). В геометрии же Вейля такое сравнение становится невозможным: если мы переносим какой-нибудь бесконечно малый материальный масштаб из Л в В, то его длина меняется, а именно, помнолсается на множитель

J((Px dxi + (jPa dxz + <Рз dx + 4>i dx),

где величины q), (p <Pz, q>i заданы во всех точках кривой, соединяющей А и В (при данной координатной системе); интеграл взят по той же кривой, следовательно, вообще говоря, может оказаться различным для различных кривых, соединяющих А v. В. Поэтому, если бесконечно малый отрезок перемещается по нек-рой кривой, а затем возвращается в исходную точку, то его длина может измениться: координатная система осталась такой же самой, однако изменился масштаб (Eichung) и поэтому все длины стали другими. Физич. законы, вырансенные в терминах геометрии Вейля, д. б. инвариантными не только по отношению к перемене координат, но и но отношению к такой перемене масштаба. Величины (pi трактуются как

электромагнитные потенциалы; если - --=0, то никакого электромагнитного

поля нет и вместе с тем J? ж^-, взятый по

замкнутой кривой, обращается в нуль, т. е. геометрия Вейля переходит в геометрию Римана. Дальнейшее развитие идеям Вейля .дал Эддингтон.

Эйнштейн в 1928 г. предложил совершенно противополоншый путь. Геометрия Римана характеризуется тем, что в ней возможно на расстоянии сравнивать длины, но невозможно сравнивать направления (отсутствует критерий параллельности на расстоянии): ели в точке А дан бесконечно малый отрезок, и мы будем переносить его параллельно самому себе в точку В, то окончательное направление, к-рое он примет в точке В, зависит от формы пути, по к-рому перемещался отрезок. В геометрии Вейля невозможно на расстоянии сравнивать ни длину, ни направление отрезков; в новой геометрии, предложенной Эйнштейном, возможно и то и другое. Это достигается след. обр.: в каждой точке четырехмерного пространства Римана даются четыре перпендикулярных друг другу единичных вектора (так наз. бай н ы); если дана определенная координатная система, то слагающие этих векторов получают

совершенно определенные значения: пусть будет v-тая слагающая s-того байна. Если дан вектор со слагающими J. в данной координатной системе, то, обозначая через Ag его проекцию на s-тый байн, получим

А^К-Л^. Решая эти уравнения относительно А^, находим

где hig-совершенно определенные (в данной системе координат и при данной системе байнов) числа. Два вектора, находящиеся на расстоянии друг от друга, считаются параллельными при равенстве соответственных Ag. Легко показать, что

(19)

Основными величинами в новой геометрии Эйнштейна являются не Qi, но lг^s. Из них

ди вьгаисляются по ф-ле (19). Гравитационные величины вычисляются с помощью этих ЙГ/д. по обычным ф-лам, а электромагнитные потенциалы по ф-лам

Все соотношения д. б. инвариантными не только по отношению к перемене координат, но и по отношению ко всем таким вращениям байнов, при к-рых параллельные друг к другу векторы остаются параллельными. Эйнштейн показал, что возможно написать такие инвариантные геометрич. соотношения, из к-рых в первом приближении получаются и закон тяготения и ур-ия Максвелла для потенциалов (ppi.

Затруднение, к-рого единая теория поля до сих пор не сумела преодолеть, состоит в том, что кроме ур-ия поля необходимо получить еще и ур-ия движения для заряженных электричеством тел. Вряд ли такие ур-ия удастся построить геометрическим путем, так как отношение^ (заряда к массе) у

те.п, состоящих из большого количества атомов, м.б. самое различное, а значит и ур-ия должны содержать эту величину, не определяемую однозначно из геометрич. данных. Если же от макроскопич. трактовки перейти

к микроскопической, где может принимать только три определенные значения (соответственно электрону, протону и фотону), то задача повидимому не сможет быть решена одной лишь О. т. (макроскопической по идеям и методам), а потребует какого-то слияния О. т. с теорией квантов (см.). Поэтому по мнению многих физиков эйнштейновская программа единой теории поля вероятно окажется невыполнимой [*].

Лит.: 1) Вавилов С. И., Экспериментальные основания теории относительности, М.-Л., 1928; Lane М., Die Relativltatstheorie, В. 1, 4 Aufl.. 1921; Einstein А., Zur Elektrodynamik bewegter Korper, АппаПеп der Physlk , Leipzig, 1905, B. 17, p. 891; Minkowski H., Die Grundglelchungen ftir die elektromagnetische Vorgange in bewegten Кбгрегп, Matli6matische Annalen , Berlin, 1910, B. 68, p. 472; 2) Einstein A., Ann. d. Pbysik*, Lpz., 1916, B. 49, p. 769; Einstein A., Sitzungsberichte d. Preus-sischen Akademie d. Wissenschaften, В., 1915, p. 831; Schwarzschild K., ibid., 1916, p. 189; D r os t e F., Verslagen , Amsterdam, 1916, v. 25, p. 163; de Sitter W., Monthly Notices of Royal Astro-

nomical Society*, London, 1916, v. 76, p. 699,- D y-s 0 n F. W., E d d i n 8 t 0 n A. S. and Davidson C, Philosopliical Transactions of the Royal Society of London , 1920, V. 220 (A), p. 291; Adams W. S., Proceedings of the National Academy of Sciences of the United States of Anierica , Washington, 1925, V. 11, p. 382; s) Einstein A., Sitzungsbe-richte d.Preussischen Akademie d.Wissenschaften ,Berlin, 19l7, p. 142; d e S i t t e r W., MonthIy Notices of Royal Astronomical Society*, London, 1917, v. 78, p. 3; Friedman A., Zeitschrift fur Physik*, В., 1922, в. 10, p. 377; Lemaitre U., Anna]es de la Soclete Scientifique de Bruxelles*, Bruxelles, 1927, t. 47, p. 4Э; d e d i 11 e г W., Proceedings of the National Academy of Sciences of the United States of America*, Washington, 1930, v. 16, p. 474; E d d 1 n g-t 0 n A. S., Monthly Notices of Royal Astronomical Society*, London, 1930, v. 90, p. 668; 4) к a 1 u z a Т., Sitzungsberichte d. Preussischen Akademie d. Wissen-schaften*. В., 1921, p. 966; Klein 0., Ztschr. fiir Physik*, В., 1926, в. 37, p. 895; M a n d e 1 H., Ibid., B. 39, p. 136; F 0 с к v., ibid., B. 39, p. 226; W e у 1 H., Sitzungsberichte d. Preussischen Akademie d. Wissenschaften , Berlin, 1918, p. 465; Eddington A. S., Proceedings of the Royal Society of London*, L., 1921, V. 99 (A),p. 104; Einstein A. , Sitzungsberichte d. Preussischen Akademie d. Wissenschaften , В., 1928, p. 217 u. 224, 1929, p. 2 u. 156, 1930, p. 19; L e V i-C 1 V i t a, ibid.,.1929, p. 137.-Ф рейндлих Э., Основы теории тяготения Эйнштейна, перевод с немецкого, М.-П., 1923; Борель Э., Пространство и время, перевод с франц., М., 1924; Хвольсон О. Д., Теория относительности Эйнштейна и новое миропонимание, 3 изд.. П., 1923; Б о р н М., Теория относительности Эйнштейна и ее физич. основы, пер. с нем.. Л., 1922; Эддингтон А., Пространство, вре.мя и тяготение, пер. с англ., Одесса, 1923; Френкель Я. И., Теория относительности, Л., 1923; Вавилов С. И., Экспериментальные основания теории относительности, М.-Л., 1928; L о-rentz Н., Einstein А., MinkovsrskiH., Das Relatlvltatsprinzip, 5 Aufl., Lpz., 1923; Weyl H., Raum-Zeit-Materie, 5 Auf., Berlin, 1923; E d-d 1 П g t 0 n A. S., The Mathematical Theory of Relativity, 2 ed., Cambridge, Г 24; P a u 1 1 W., Relativi-tatstheorie, Enzyklopadle cer mathematischen Wissen-schaften. Band, 5, T. 2, H. 4, Leipzig-Berlin, 1922; v. L au e M., Die Relativltatstheorie, B. 1, 4 Aufl., 1921, B. 2, 2 Aufl., Brschw., 1923; Becquerel S., Le principe de relativite et la theorie de gravitation, Paris, 1922; Silberstein L., The Theory of Relativity, 2 edition, London, 1924; Bauer H., Mathe-matische Einluhrung in d. Gravitationstheorie Ein-Steins, Wien, 1922. M. Бронштейн и В. Фредерике.

0. Т. И философия. О. Т. пробудила к себе исключительно большой интерес со стороны философов, а также в самых широких и разнообразных кругах неспепиалистов. В настоящее время существует огромная литература как популярная, так и философская, посвященная О. т.; необходимо однако отметить, что в популярной литературе самое содержание теории искажается часто до неузнаваемости. В СССР усиленно дискутировался вопрос об отношении О. т. к основам материалистич. диалектики. В этом отношении наметилось два течения: одни (И.Е. Орлов, А. К.Тимирязев, Г.А.Харазов, 3. А. Цейтлин) считают основные положения теории несовместимыми с материалист, диалектикой, другие (А. Гольцман, Б. Гессен, Ю. Семковский, В. Юринец, А. А. Максимов, О. Ю. Шмидт) полагают, что О. т. является реализацией в конкретной форме учения диалектич. материализма о пространстве и времени. Через Лоренца в лице Эйнштейна физика наконец пришла к идеям, приближающим к усвоению на пространство и время точки зрения диалектич. материализма. Однако Эйнштейн дал свои мысли, как и Гегель, в идеалистич. формулировке И- В области физики взгляды Эйнштейна на пространство, время и движение являются конкретизацией диалектич. концепции пространства и времени [J. Правда, и это тече-

ние среди философов-марксистов вынуждено признать, что оболочка теории насквозь идеалистическая, что за нее ухватились все философы-идеалисты, пытающиеся с помощью этой теории опровергать материализм; однако при этом указывается,что идеалистич. налет можно легко устранить, что он органически не связан с самой теорией.

Рассмотрим, что в О. т. послужило поводом для идеалистич. выводов и насколько эти поводы являются посторонним, наносным элементом, не связанным с самой теорией. О. т. исходит из предположений, что движение относительно в абсолютном смысле, т. е. что нет возможности узнать, что на самом деле движется: человек ли идет по земле, или земля уходит из-под человека в обратном направлении Для того чтобы формально провести эту точку зрения, надо допустить, что у наблюдателей движущихся различно по отношению друг к другу, свое особое время, свои пространственные отношения и свое определение об одновременности, не совпадающее с определением об одновременности для другого наблюдателя. Отсюда философ-идеалист проф. Вильдон Карр делает вывод, что современная наука не признает единого мира с его пространством и временем, что не существует единого объекта материального-пространственно-временного мира, но зато существует множество субъектов [*]. Сам Эйнштейн признает в одном из своих основ-, ных сочинений [*], что руководящей идеей его было стремление облечь в математич. форму мысль Маха о том, что системы Коперника и Птолемея с научной точки зрения вполне равноправны, и что система Коперника имеет лишь преимущества удобства . Неудивительно поэтому, что проф. .Филипп Франк, на съезде физиков осенью 1929 г., договорился до оправдания инквизиции в^ ее процессе против Галилея: В точке зрения инквизиции можно найти нечто соответствующее точке зрения современной О. т., согласно которой нельзя сказать, что земля на самом деле движется, а солнце стоит, но можно только утверждать, что описание явлений в координатной системе, для которой дело обстоит именно так (т. е. земля движется), выходит проще . Нельзя сказать, чтобы эта точка зрения отличалась новизной: мы ее встречаем в весьма отчетливой форме, сформулированной в иредис-ловии Оссиандера (А. Hossman) к знаменитому труду Коперника, опубликованному в 1543 г. Признание одного только относительного движения приводит к серьезным трудностям; нанр., если в детской игре запустить быстро вращающийся кубарь, то с точки зрения О. т. возможны два варианта: или кубарь вертится на земле, или земной шар со всей солнечной системой и системой Млечного пути вертится в обратную сторону. Конечно всякий релятивист скажет, что экономнее думать о вращении кубаря, но теоретически оба случая равноправны. А если это так, то спрашивается, можно ли говорить об однозначности энергии: ведь в случае вращения кубаря или всей вселенной эне,ргия движения будет весьма и весьма, различйой. Можем ли мы при признании хо~