• Что такое фактурная штукатурка
• Выбираем сухие строительные смеси
• Преимущества напряженного железобетона
• Что влияет на выбор кровельного материала
• В чем преимущество пробковых полов

1925, V. 63, p. 1046; ) G й. b о г, Kathodenoszillo-graph, Archiv fur Elektrotechnik , Sonderbeft der Forschungshefte der Studiengesellschaft fur HOchs-spannungsanlagen, Berlin, 1927, H. i; Щ George, R. H., A New Type of Hot Cathode Ray Oscillograph, JAIEE , 1929, p. 534; ) S о m m e r f e 1 d A., Uber ein Kathodenoszillograph hoher Spannungsempfindlich-keit, Archlv fur Elektrotechnlk , Berlin, 1928, H. 5/6, p. 607; Щ R 0 g 0 w s к у W. und Baumgart, Ein Gluhkathodenoszillograph fixr Vakuumaufnahmen, ibid., H. 4, p. 521; 18) В e к Ш и H с к и Й С. А., Электросвязь , Ленинград, 1927, 3, стр. 9-14; i*) Н а z е н а. К е п у о п, Priniary Radio Frequency Standartisa-tion by Cathode Ray Oscillograph, Bull. Bureau of Standards*, 489; Щ The Electrician*, L., 1924, v. 92, p. 631; ) Г. П. 162725; 17) P e t e г s J. F., oElectr. World*, N. Y., 1924, v. 83, p. 769; L e e E. S. a. Poust C. M., JAIEE , 1927, v. 46, p. 149; M u 1-ler-Hillebrand, Slemens Zeitschrift , Berlin, 1927, Jg. 4, p. 547.-с текольниковИ. С, Катодный осциллограф, Вестник экспериментальн. и теоретич. электротехники , М., 1929, т. 2, J-i (имеется библиография).

ОСЦИЛЛЯТОР, в общем смысле любая колеблющаяся система. В теоретической физике обычно О. назьшают линейную колеблющуюся систему, например электрон, совер-шаюпщй колебания по прямой линии относительно определенного положения равновесия. Если сила, заставляющая О. колебаться, пропорциональна удалению от положения равновесия, то О. назьшают гармоническим, или квазиупругим, в противном случае О. будет ангармоническим. Гармонич. О. является простейшей идеализированной моделью колебаний в атома,х и молекулах и постоянно применяется при рассмотрении процессов распространения света в веществе и т. д. Ур-ие движения О. в классич. механике выражается так:

(ж-смещение,m-масса, к-постоянная квазиупругой силы). Решение этого уравнения чисто гармоническое:

x = Asm{y]-t + a). (2)

Частота колебаний отсюда

271 У тп

она (в этом теоретич. простота О.) не зависит от энергии движения, или амплитуды А. Энергия О. равна кинетич. энергии его при прохождении через положение равновесия (потенциальная энергия здесь равна нулю):

Е = А^==2лтсоЫК (4)

В теории квантов (см.), развитой Планком и Бором, вопрос о колебаниях О. получил иное освещение. По основному постулату Бора, фазовый интеграл:

(где р - импульс, h - постоянная Планка, п=0, 1, 2, 3, ...). Из ур-ий (2), (3) и (4) следует, что для о. 1 = , т. е.

Е = nhco, (6)

иными словами, энергия О. должна быть кратной целого кванта kco.

В новой квантовой механике теория О. изменяется. Основное волновое ур-ие Шре-

дингера (см. Кванты) принимает в данном случае вид:

у = 0.

E=(n + ~jhm.

Непрерывное и исчезающее в бесконечности решение этого ур-ия возможно только для дискретного ряда значений энергии:

В отличие от прежней теории квантов (6) здесь входят половинные значения кванто вых чисел. Этот результат согласуется с экспериментальными спектроскопическими данными.

Лит.: Д а р р О у К., Введение в волновую механику Шредингера, УФН , 1929, вын. 9, стр. 437; So mm erf eld A., Atombau und Spektrallinien, Wellenmechanischer Erganzungsband, Braunschweig, 1929; Planck M., Vorlesungen uber d. Theorie d. Warmestrahlung, 5 Aufl., Lpz., 1923. C. Вавилов.

ОСЬ в м a ш И но строении, деталь, на которой укрепляют вращающиеся части машин и которая осуществляет их геометрич. ось вращения. В отличие от вала О. не передает крутящих усилий и подвергается нагрузке только от веса посаженньгк на нее частей и от тех сил, которые приложены к этим частям. Конструктивно различают О вращающиеся вместе с наглухо посаженными на них частями, и О. неподвижные, служащие лишь опорой для свободно посаженных на них и вращающихся тел. Неподвижные О. подвергаются действию нагрузки, не меняющей своего направления; вращающиеся О. подвергаются действию изгибающих сил, все время меняющих по отношению к О. свое направление. Те части вращающейся О., к-рыми она опирается на опоры (подшипники), назьшаются цапфами, или шипами, если они расположены по концам оси, и шейками, если расположены где-либо по середине оси. Если главная нагрузка направлена вдоль оси, то опорный ее конец называется пятою. Опоры, поддерживающие шипы или шейки О., осуществляют вращательную пару. Для предотвращения продольного относительного перемещения шипы снабжаются заплечиками; для правильной установки целесообразнее снабжать один шип двумя заплечиками, другой же заплечиками не снабжать. В отдельных случаях, учитывая специальные условия работы,предусматривают возможность нек-рого продольного разгонаО.

Шипы оси выполняют цилиндрической, а реже конической формы. При силе Р кг, действующей на шип, среднее напряжение р кг/см на изнашивание определяется из

ур-ия р = 1, где I-длина шипа в сл* и d его

диаметр в см. Напряжение р не распределяется равномерно по поверхности шипа, но изменяется как по его длине, так и в зависимости от положения точки поверхности на окружности шипа. На фиг. 1, А даны диаграммы напряжений в каждой точке шипа для шипа длиною 1= 400 мм и d= 200 мм при 3, ООО об/м. для различных средних давлений рдр , диаграмма А относится к сечению, проведенному через середину длины шипа, а диаграмма Б - к сечению на расстоянии 50 мм от края. Распределение давления в зависимости от окружной ско-

ростн при одном и хож же среднем давлении р^=6,5 кг/см дано на фиг. 2, А и Б для того же шипа и для тех же сечений. Коэф. трения Ml шипа О. зависит от ряда факторов; согласно исследованиям Гюмбеля:

, = 0,0023/.f ;

-кг-ск/м^-абсолютная вязкость смазки, п-число об/м. О. и I-коэф., зависяш;ий от положения шина в подшипнике и от отношения наименьшей толщины слоя смазки к зазору между шипом и подшипником. По . исследованиям Фивега шип перемещается относительно подшипника в зависимости от числа оборотов, и только при числе оборотов п=оо О. шипа совпадаете О. подшипника. Если D - диаметр подшипника и d- диам. шипа, то зазор s = D- d; при покое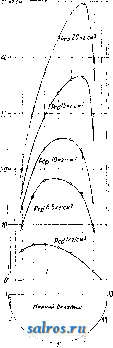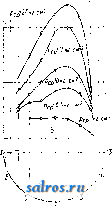

Фиг. i .

эксцентриситет е О. шипа и подшипшша будет = S см; при вращении О. шипа будет перемещаться по некоторой кривой АВМ (фиг. 3), где М - центр [подшипника и

AM = 2. При покое О. шипа находится в А,

при п=ос-в Ж; при нек-ром числе оборотов О. шипа займет положение В, которое определится уг-,лом /5; в этом случае наи.меньшая толщи-

иияний ьклодыа

Фиг. 2.

я J3

на смазки будет равняться ве.чичине h. По Гюмбелю положение О. шипа определяется

191 ОООР -82 d + l

Эти величины Ф, будут[и изображены в полярных координатах угла /3, дают кривую EDM. Определив значение Ф и проведя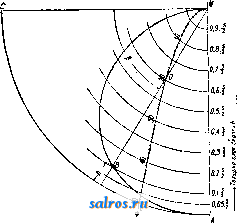

Фиг. 3.

прямую через Ж и точку кривой EDM, соответствующую найденному значению Ф, до пересечения с кривою АВМ пути центра шипа, определим искомую точку В положения О. шипа и наименьшую толщину h слоя смазки.

В табл. 1 сведены результаты опытов дающих значения Ф, угла и коэф-та

в зависимости от отношения ~.

Табл. 1. - Зависимость ф, угла /Зико-

эфициента I от -.

Из таблицы следует, что наименьшее значение § = 2,05 получается при отношении

= 0,5; при этом значении коэф. трения

/wn = 0,0047 / ./fri;

в среднем можно считать = 2,4 и

, ,0,00.о5Л^-Л^П.

Зависимость коэф-та трения от числа оборотов и давления характеризуется диаграммой фиг. 4, вычерченной для шипа, опирающегося на подшипник Селлерса-с кольцевой смазкой. Резкое увеличение значения ft при

малых числах оборотов объясняется недостаточной толщиной h смазки, в виду уве-

Окружная скорость

iTpemte по сухоту

Схема

-Ap-lKZ/CM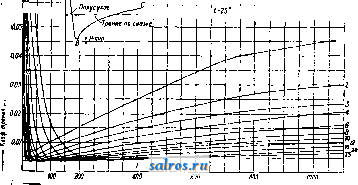

опасным местом в смысле возможного излома является сечение у корня шипа, которое подвергается дейст-41ск ВИЮ изгибающего момента = = fcH где fc-

допускаемое напряжение на изгиб в кг/см и Wcm- момент сопротивления сечения, равньш - , следовательно для d получим:

5Р( кь

а так как

d у 5р

► ixCAo оборотов п 8 мин

Фиг. 4.

личения эксцентриситета оси шипа и подшипника, так что шип работает полусухим. Кроме того коэф. fix зависит от t, от системы смазки, от формы и материала подшипника. Секундная работа Ац трения будет равна

Ат>=Р- fi- - 0) = Р /Лл - V = р-1 d - fii - V.

Удельная работа трения, т. е. работа, отнесенная к единице поверхности шипа, равняется

Работа трения почти целиком превращается в теплоту, причем количество Q теплоты, вьщеляемой в 1 ск., будет равно

427

При расчете шипов

Cal/CK.

последние проверяют на среднее давление Р = величина

р для тех случаев, когда имеет место полусухое трение (фиг. 4), при работе стали по бронзе берется равной 50 кг/см, для закаленной и шлифованной стали по бронзе р= =80 кг/см и для той же стали по баббиту р = 90 кг/см. В тех случаях, когда износ шипа не играет роли, эти величины м. б. взяты в 2-3 раза большими. Для паровозньгх О. допускают р = 150-300 кг/см. Наиболее

В табл. 2 приведен ряд значений напряжения fc в зависимости от давления р и от отношения .

Для того чтобы шип О. не нагревался выше допустимой нормы, необ-t ходимо, чтобы все обра-

зуемое тепло было от шипа отведено; а так как для Од имеет место след. соотношение:

PfiiV Vii-i ndn 1 л\ л 60 100

где V дано в м,ск и d в см, то

Р W * 2 * 100 ~ 200г ~ id 60

и длина шипа должна быть не меньше I - Рп

~ 200pi? ~ 2000ро

В зависимости от условий работы допускают различные значения для pv, напр. для ва-

гонньгх О. рг;50 , для паровозных О.

смз ск

Расчет 0. 1) Случай статически определимой О. (фиг. 5). Для определения сил реакций А я В подшипников построим силовой многоугольник с полюсным расстоянием Н; строя веревочный многоугольник (см.) AiCjBiBi и проводя далее из полюса О луч, параллельный ABi, получим величины сил реакции А и В подшипников. Величина изгибающего момента для каждого сечения О. определяется как произведение из ординаты веревочного многоугольника на, полюсное расстояние Н, на величину mfe масштаба сил и на величину nif, масштаба длины. В точке С изгибающий момент

Табл. 2.-3 начения напряжения кь в зависимости от pnJ/dCB кг/см).

ОСЬ

Мб = CiCz H-mi-mj,. Для любого другого сечения оси на длине участка АС изгибающий момент будет равен А-х; если нужно спроектировать ось равного сопротивления, то пользуемся ур-ием:

Ах Ах-10 10 Ад:

= Const,

где г радиус сечения; следовательно

ryi5f = k7x,

т. е. при осях равного сопротивления радиус последней будет изменяться по закону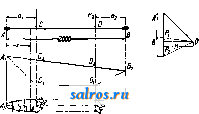

Фиг. 5.

кубич. параболы; это будет справедливо для всех тех участков О., для которых ординаты веревочного мн-ка ограничены прямыми линиями. Вершина параболы для участка АС будет лежать на вертикали, проходящей через точку J.i пересечения сторон С-А- и CgJ-i веревочного многоугольника, для участка В£>-на вертикали, проходящей через точку и для участка О. СВ-на вертикали, проходящей через точку В.. Для определения диаметра всех сечений О. достаточно определить диаметр в сечениях С и D; деля затем О. параболы на одинаковое число частей, например на 10 ч., определяют соответствующие диам. из ур-ия d= d -у ~,

где X-длина в долях всего участка; на основе этого уравнения составлена следующая зависимость d от х:

размеров, пунктирная кривая дает параболу равного сопротивления. Пользуясь этим методом или чисто аналитически, легко можно рассчитать оси, нагруженные в одном месте вне опор (фиг. 7).

Фиг. 7.

2) Расчет статически неопре-делимойО. При расчете статически неопределимых О. предварительно задаются размерами О. на основе опыта и наблюдений над работающими О. или определяют размеры О. по одному из приближенных способов расчета и затем производят поверочный расчет по нижеуказываемому методу. Сущность поверочного расчета статически неопределимой О. заключается в следующем: если напр. у О., лежащей на трех опорах отнять средний подшипник, то О., прогнувшись, даст в этом месте стрелу прогиба 6 сила реакции С среднего подшипника предотвращает этот прогиб, как это схематически изображено на фиг. 8. Для онреде-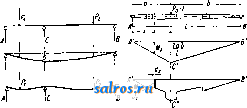

При конструктивном выполнении в целях облегчения обработки отдельные участки О. выполняют не параболическими, а коническими, причем те места О-., на к-рые д. б, посажены детали, выполняют цилиндриче-

Фиг. 6.

скими. Эти части О. назьшаются насадками. Диаметр насадки D выполняется равным d-\-2f, где d-расчетный диаметр О. в данном сечении и/=з^ -Ь 2 мм (фиг. 6). На

фиг. 6 дано изображение конструктивного очертания оси суказанием относительных

Фиг. 8.

ления величины С рассмотрим действие силы pQ=l кг, приложенной взамен С; в этом случае величина прогиба д в любом сечении^ отстоящем на расстоянии х от середины левой опоры,м. б. определена из следующего ур-ия:

где а-коэф. удлинения,. Jx-момент инерции сечения оси. Построив для силы Ро = 1 кг веревочный мн-к А'В'С, можно но его ординатам, дающим величину М^, подсчитать

выражение и построить соответствующую этому последнему выражению диаграмму А В С .

Беря элементы площади ~ dx по диаграмме д^В^С и представляя эту элементарную площадь

Фиг. 9.

В виде некоторой силы, приложенной в ц. т. элемента площади, можно построить для этих элементарных сил силовой и веревочный мн-ки, ординаты которьгх и дадут в масштабе величину прогибов для каждого сечения О. Полученный таким путем веревочный мн-к является упругой линией для на-

грузки в точке С рассматриваемой О. Согласно теореме Максвелла упругая линия для нагрузки в точке С является в то же время линией влияния (см.) для той же точки С и дает возможность определить силу реакции в этой точке; т. е. если сила Ро = 1 кг, приложенная в точке С, вызывает прогиб в точке D, равный Уд (фиг. 9), то та же сила Ро=1 кг, будучи приложена в точке D, даст прогиб в точке С также равный у- Если в точке D будет приложена сила Pi кг, то прогиб в точке С будет равен Pi-у о Следовательно для того случая, когда на ось будут действовать силы Pi и Pg, сумма их действий должна yp9,BH0Bie-шиваться влиянием силы реакции С, т. е.

Ct/(7=Pi2/i + Pa2/2, или, в общем виде,

C.2/.= Sp?/; С = .

с

Для случая, когда сила Р приложена снаружи опор А или В, в расчетное уравнение соответствующую ей ординату Уп (фиг. 9) вводят с отрицательным знаком. Для примера на фиг. 10 дано в масштабе графич. определение силы реакции среднего подшипника для О., нагруженной силами Pi=2 500 кг и Р2= = 1 800 КЗ. Масштабы построения указаны непосредственно на чертеже. Порядок построения следующий: строим для силы Ро=1 кг силовой многоугольник (план сил) с полюсным расстоянием Н=5 ем (фиг. 10, С), после этого строим веревочный мн-к, А'С'В', который является эпюрой моментов СФиг. 10, D), а затем

эпюру =Д; при построении

носят полученное значение на ту же вертикаль, проходящую через Ро, - и полученную точку соединяют с и В до пересечения с соответствующими ординатами взятых се-

эпюры для частей О., имеющих одинаковые моменты инерции J, напр. для трех шеек А, В я С, имеющих 0=75 мм, достаточно отложить

величину р' на вертикали, проходящей

через точку приложения силы Р, лученную точку С соединить прямыми с точками А п В , эти прямые ограничат площади

для всех сечений с одина-

ковыми моментами инерции J, т. к. изгибающий момент М^. изменяется от А' до С по закону прямой. Аналогичным способом определяют значения для конических частей оси; опре-

Х

делив для сечения по середине конич. части (напр. для сечения с диам. 92,5), на-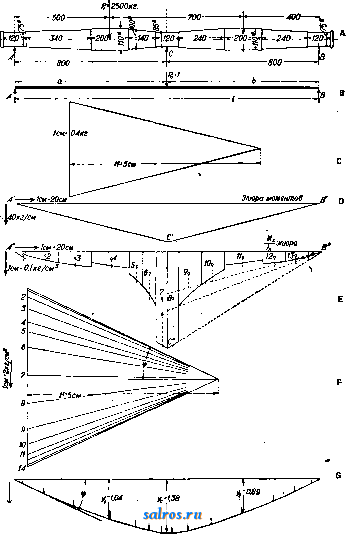

Фиг. 10.

чений, как это изображено в правой части фиг. 10, Е. Для данного примера достаточно определить - (в кг/см) для следующих пяти диаметров О.:

Построив эпюру ц^, делим [площадь ее на

14 ч. и по полученным [площадям строим силовой мн-к (фиг. 10, F), по к-ромуполучаем упругую линию, или линию влияния, для с от силы Ро=1 кг. Для данного примера и данньгх масштабов 2/i=l,04, Уа=0,89,

Ус = 1,38 см, откуда получаем следующее значение С:

PiVi + PiVs 2 500 1,04 + 1 800 0,89

1,38

= 3 050 кг.

После определения С, силы реакции Л и В легко определяются из ур-ий моментов.

В том случае, когда О. имеет более трех опор, то предполагая опоры С я D отнятыми, строят две линии влияния I я II для единичной нагрузки в С или в D (фиг. 11) и получают два расчетных ур-ия:

с

/с

Фиг. И.

С.у'; + Вуо=Ру ; из этих уравнений и определяют силы реакции С и D.

0. паровозные, тендерные и вагонные. Паровозные О. в завивимости от их назначения

разделяют на в едущие, непосредственно связанные с шатунами .сцепные, связанные с ведущими О. при II помощи спарников, и бегунковые (см. Паровозы). Ведущие и сцепные оси подвергаются как изгибающим, так и скручивающим усилиям. Материалом для изготовления пря-мьгх паровозных О. служит мартеновская сталь (марка Ст5 повышенная) с врем, сопротивлением на разрыв Л > 5 ООО кг/см и относительным удлинением 20% (содержание фосфора допускается> 0,07%); для ко-ленчатьгх О. применяют также никелевые и хромоникелевые стали с временным сопро-тивлением^б ОООкг/см и относительньпд удлинением > 18%. Выкованные из болванок заготовки после отжига поступают для обточки на токарные станки. Обточке подвергается вся поверхность пря-мьг£ О., шейки полируют и накатывают. При изготовлении прямых О. на каждой О. должен быть с головной части болванки предусмотрен припуск для изготовления пробы; для не-скрльких О., выковываемых из одной болванки, достаточно иметь один припуск; для коленчатых О. припуски обязательно оставлять с обеих сторон оси. О. без припусков приемке не подлежат. На каждой О. д. б. выбита марка з-да, время изготовления, номер плавки и литерные обозначения изготовленной О., а именно: В-на О., изготовленной из верхней части общей болванки или из одиночной болванки; ВВ-для следующей О. из той же болванки, ВВВ-для третьей О.; литерные обозначения ставят у конца, соответствующего верхней части болванки; кроме того на О. выбивается заводской номер О. В центре О. должны быть просверлены от-

верстия глубиною 20 мм, 0=-6 мм с расточкой на конус в 60°. При Изготовлении паровозных О. для ж. д. СССР допускаются следующие отступления от размеров чертежа. Для прямых осей в черном виде: по длине -f25 мм, по диам.-f 5 мм; для полуобточенных осей-в местах полуобточенных по диам. Ч-З лин; для окончательно обработанной О.: но длине+2 мм, по диаметру шеек4-0,2 мм, по диаметру под ступичной части -fl мм, по длине шеек4-0,5 мм, по расстоянию между внутренними бортами шеек±0,5 jhjh, по диам. средней части4-2 мм, по диам. буртов 4-0,5 мм, по радиусу галтелей +1 мм. Для О. коленчатых то же, что и для прямых О. и, кроме того для поперечных размеров колен 4-2 мм и по радиусам колен ±1 мм. Образцы паровозных О. должны быть подвергнуты исныганиям на разрьш и на удар. Длинный образец (0=20 мм, длина 1=50 мм) должен показать В^Ъ ООО кг/см, г^28%; для испытания на удар -становлены: вес бабы в 25 кг, высота падения 2 м, расстояние между опорами 160 мм. Образец выполняют квадратного сечения 30 х 30 мм и длиною 200 мм; после 15 ударов бабою не д. б. надрьгоов, трещин, изломов и других пороков. О. вагонные и тендерные могут иметь следующие допуски в черном виде; по диаметру средней необтачиваемой части 4-5 и -1 мм, по диаметру обтачиваемых частей 4-5 мм, по длине 0.4-15 мм; в чистом виде: по диаметру в частях необтачиваемых4-5 и -1 мм, по диам. шейки -Ь0,5 мм, по длине шейки4-1 мм, по толщине буртика +2 мм., по диам. буртика 4-2 мм, для расстояния между серединами шеек ±1 мм, по диам. под-ступичной части 4-1 мм. Испытание О. ши-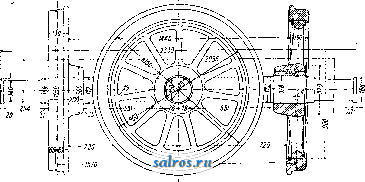

Фиг, 12.

рокой колеи в целом виде производят на удар пятью ударами бабы весом в 1 ООО или 500 кг, падающей с высоты Н, определяемой из уравнения PH=aD, где Р-вес бабы в кг, Н-высота в м, D-диам. середины О. в мм, а-коэфициент, равный 0,20 для бабы весом в 1 ООО кг и 0,18 для бабы весом в 500 кг. Расстояние между опорами 1,5 м; после 1-го и 3-го удара О. должна быть повернута на 180°. О. узкой колеи испытывают пятью ударами,бабы весом в 500 ке с высоты Я=0,054 Djl, где П ъ м, D-диам. средней части в мм, I-расстояние между опорами, равное ширине колеи в см. На фиг. 12 дано изображение и указаны раз-

ОСЬ

меры вагон. О. американского типа D, на фиг. 13-пассажирской нормальной О. Расчет О. представляет затруднение вследствие того, что неизвестны в точности величины действующих сил, в том числе и величины силы давления рельса на реборду колеса во время хода поезда по закруг-.лению.При расчете принимают, что боковая сила К=0,4:Р, где Р-нагрузка на О. в спокойном состоянии. Под действием силы if давление на шейку О. увеличит-

ся на величину р=- К

и сила давления на колесо увеличится на ве-

-личину q=±l K,

где D-диам. колеса,

й-высота ц. т. вагона над серединою О.,

s - расстояние между точками опоры колес.

Табл. 3.-Размеры вагонн

парных вагонов, -напряжение на изгиб в подступетной части 400 кг/см для пассажирских вагонов и:$560 кг/см для товарных вагонов. Основные размеры вагонных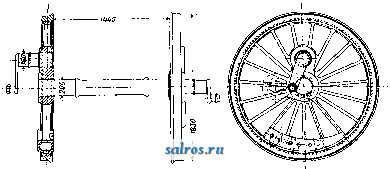

Фиг. 14.

осей на железных дорогах СССР представлены в табл. 3 (в мм.).

ых осей на дорогах СССР.

L - расстояние между серединами осевых шеек. Зная силы Р, К, р ж q, ведут расчет О. на изгиб, проверяя сечения у корня шейки, у основания подступичной части и сечение по середине длины оси. Для определения предельных размеров осевых шеек и подступичной части можно пользоваться следующими рекомендуемыми НКПС формулами: =81: nkiP и = 161: пку^Р, где d -диам. шейки, -диам. подступичной

Паровозные оси, ведущие и сцепные, для паровозов с внутренней рамой и с цилиндрами, расположенными снаружи, имеют очертание, изображенное на фиг. 14, Ведущие и сцепные О. подвергаются при работе изгибу от веса паровоза и от силы давления пара на поршень,передаваемой на ведущие колеса с помощью шатунов и спарников. Размеры шеек определяют по формулам для Wk: для ведущей оси:

Wk = j/ \Pl + 0,4(Р + 1 ООО) + [0,ЗРг + -f p,(l,- )J + (0,15Р DY;

для сцепных осей:

части, I-длина шейки, 1-расстояние се-Hfcj = У^Грг + о,4(Р-Ы

ООО) +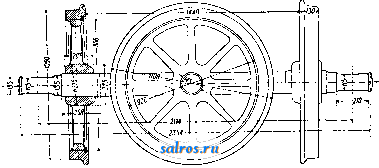

Фиг. 13.

редины шейки до круга катания, fcjg - напряжение на изгиб в шейке < 550 кг/см для пассажирских вагонов и 700 кз/сж для to-

т. У. т. XV.

0,spi + fpk- + (0,15Р ВУ;

для бегунковых осей: Wkj, = Рг -f 0,4(Р-н + 1000)f,

гдеР-сила статич. давления колеса на рельс в кг, I-расстояние от середины шейки до круга катания в см, l- расстояние от середины шейки О. до геометрич. О. цилиндра в см, 1- расстояние от середины шейки оси до середины сцепной цапфы, р^.- давление пара в котле в кг/см и do-диаметр парового цилиндра в см, D-диаметр колес по кругу катания в см, п-число спаренньгх О.; kf,-допускаемое напряжение на изгиб

1 ООО кг/см для ведущих и 700 кг/см для сцепных ибегунковых осей, W-момент сопротивления сечения О. в см. Предельные напряжения изношенных ведущих осей

< 2 ООО кг/сж2, для сцепных и бегунковых

< 1 700 кг/см. Боррис дает эмиирич. ф-лы: для ведущей оси:

d = 6i/P(jD-b500), для бегунковой оси:

d = 63]/P,

где d-диам. шейки оси в мм, D-диам. колеса в мм, Р-нагрузка от веса паровоза на О. в т. При упрощенных расчетах при-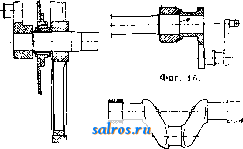

Флг. 15.

Фиг. 17.

нимают W=0,1 d для сплошной оси и W= 0,1 (d-dl) для полой. Диам. под ступичной части выполняют больше диам. новой шейки на 8-10 мм; диаметр средней части

Фиг. 18.

оси меньше диаметра подступичной части на 10-15 мм. На фиг. 15 и 16 даны конструкции О. для паровозов с внешней рамой, в этом случае О. снабжается кривошипом; конструкция О., изображенной на фиг. 16, имеет относительно меньшую длину, но зато наиболее опасное сечение а недоступно

Фиг. 19.

осмотру, т. к. для осмотра нужно каждый раз снимать кривошип, что невозможно. Конструкция ведущей оси для паровоза с тремя цилиндрами, из которых один лежит внутри рамы, дана на фиг. 17. Ведущая О. 4-цилиндрового французск. паровоза изо-

бражена на фиг. 18. Для предотвращения появления трещин в наиболее трудно проковываемой части ab щек О. последние выполнены с вырезами с, так что крутящие усилия передаются через хорошо прокованные части щек О. Трудность отковки таких осзй привела к изготовлению коленчатых паровозных О. из нескольких отдельно выкованных и затем соединенных частей. Примером может служить О., изображенная на фиг. 19,. составленная из трех частей а, b и с. Конструктивное выполнение-см. также Паровозы..

Лит.: Сидоров А. И., Курс деталей машин, ч. 1, 2 изд., М.-Д., 1927; Б о б а р ы к о в И. И., Детали машин, часть обш;ая, М.-Л., 1926; К е с т-нер Е. г., Курс паровозов, М., 1922; К е с т н е i> Е. Г. и Николаев И. И., Динамика и парораспределение паровозов, М., 1931; R.otscher Е.,. Maschinenelemente, В. 2, В., 1929. Б. Шприн .

ОТВЕС, приспособление, состоящее из: тонкой бечевки и грузика на конце ее, позволяющее судить о правильном горизонта.11ь-ном или вертикальном положении нек-рых частей. инструментов и принадлежностей к: ним. От действия силы тяжести бечевка, называемая нитью О., принимает вполне-определенное постоянное направление, называемое отвесной линией. Оконечность грузика должна точно находиться на продолжении натянутой бечевки; для этой цели грузику придают вид опрокинутого конуса, поставленного на цилиндр; в основание цилиндра ввинчивается маленький цилиндрик так, чтобы центры их совпадали:, в центральное отверстие последнего пропл- скается бечевка с узлом на конце (фиг. 1).. Для более быстрой установки нити в отвесное положение применяется двойной отвес с противовесом d (фиг. 2). Для центрирования мензулы (см.), т. е. для установки точки на планшете мент зулы над определенным пунктом на местности (на одной отвесной линии с ним), О. прикрепляют к вилке, сделанной из дерева или из металла и состоящей из трех планок А, В я С. Планки А я С скреплены неподвижно, а планка В (длиннее А) вращается на шарнире с. Нить с грузиком О закрепляется у нижней планки В; ее продолжение bb проходит через носик Ь' верхней шпанки А, когда В отогнута и планка А горизонтальна. Чтобы -йЭ\ -\ J- произвести центрирование мензулы, ее сначала центрируют и устанавливают в горизонтальное положение на-глаз. Затем вилку кладут на планшет так,чтобы ббльшая часть планки А помещалась на. планшете. Удерживая носик вилки у центрируемой точки на планшете, передвигают планшет по подставке мензулы до тех пор, пока вершина конуса О. установится над точкой местности (будет- бить в точку местности), означенной колом или иным образом. Вилка применяется при съемке мензулой в масштабе 1 /1 ООО и круп-

Фиг. 1.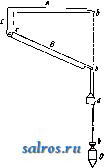

Фиг. 2.

нев;при съемках же в мелких масштабах центрировку мензулы производят на-глаз, без вилки, так как в этих случаях погрешность, которая происходит от неправильной центрировки над точкой стояния, не превосходит предельной величины отрезка прямой на плане, которую можно различить невооруженным глазом (так назыв. графической точност и).Кро-ме указан, применений О. пользуются при нивелировках для установки реек в вертикальном положении. Отвес применяется также в простейшем нивелире-ватерпасе (см.) и в угломерных инструментах для] установки центра лимба (см.) над точкой местности. Недостаток отвеса тот, что им нельзя пользоваться при сильном ветре.

ОТДАЧА АРТИЛЛЕРИЙСКИХ ОРУДИЙ, импульс силы давления пороховых газов на затвор орудия, равный количеству движения, приобретаемого орудием в процессе выстрела. По закону сохранения движения ц. т. свободной группы тел остается в покое или движется прямолинейно с постоянною скоростью до тех пор, пока действующие силы, перенесенные в ц. т. группы, остаются в равновесии. Закон этот применим ко всякому огнестрельному орудию, т. к. калг-дое из них можно рассматривать как группу тел (снаряд, само орудие и т. д.), взаимное положение к-рых изменяется под влиянием сил давления пороховых газов, т. е. сил, которые, будучи перенесены в ц. т. группы, остаются в равновесии. Силу трения орудия о землю, не превышающую в обычных условиях 0,01 доли силы давления пороховых газов, можно не принимать в расчет. Если орудие перед выстрелом находилось в покое, то и во время выстрела ц. т. группы останется в покое, т. е. перемещение тел группы будет происходить во взаимно-противоположных направлениях и расстояние каждого из них от начального положения будет обратно пропорционально массе этого тела. Если например масса орудия в 100 раз больше массы снаряда и тел, движущихся вместе с ним, то перемещение снаряда вперед будет приблизительно в 100 раз больше перемещения орудия назад. Это движение орудия-явление нежелательное.

В интересах правильности наводки, скорости стрельбы, избежания наката и новой наводки после каждого выстрела и т. д. необходимо было бы, чтобы орудие оставалось во время стрельбы неподвижным. Требование это практически невыполнимо, так как давление пороховых газов, обусловливающее движение орудия назад, настолько велико, что для закрепления последнего в неподвижном состоянии потребовались бы чрезвычайно прочные сооружения. В поЛевых орудиях напр. сила давления норохов. газов обычно превышает 125 ООО кг. В условиях, при к-рых приходится действовать полевым орудиям, никакое закрепление их в неподви-

жном состоянии при этих громадных силах давления невозможно. Величина движения орудия назад во время выстрела обусчов-ливается двумя факторами: действием силы давления пороховых газов и продолжительностью этого действия, т. е. импульсом давления пороховых газов, передаваемым орудию в направлении, противоположном движению снаряда. Импульс этот, называемый отдачею орудия, выражается интегралом

где Р-сила давления пороховьгх газов и t-продолжительность в ск. действия ее на орудие. Сила Р определяет собою величину ускорения двинения орудия во время выстрела и равна ~ W, где G-вес орудия в

кг, д-9,81 mjck-ускорение силы тяжести и W м/ск-ускорение движения орудия. Таким образом:

t t t

JPclt о

WdtC dv=v, (1) g gj g

где V м/ск-скорость, приобретенная орудием к концу выстрела. Отдача орудия равна следовательно тому количеству движения, которое приобретает орудие к концу выстрела.

Энергия пороховых газов тратится на движение орудия, снаряда, самих пороховых газов и того воздуха, к-рый находится в канале ствола до выстрела. Т. к. до и после выстрела канал ствола оказывается заполненным приблизительно одинаковым количеством газов, то в дальнейшем расчете влияние воздуха в канале ствола на отдачу можно не принимать в соображение. Такой же по величине импульс, который передается пороховыми газами орудию, передается ими такле массе снаряда и пороховых газов. Как и в предыдущем случае, оказывается, что импульс силы давления пороховых газов равен тому количеству движения, к-рое массы снаряда и пороховых газов (вес последних равен весу порохового заряда) приобретает к концу выстрела, т. е.

О О

где Q-вес снаряда, V-скорость, с которой снаряд вылетает из ствола орудия, р-вес порохового заряда и U-средняя скорость, с которой пороховые газы оставляют канал ствола. ВеличиныQ,VHp для всякого орудия точно известны, тогда как скорость U лишь с большим трудом поддается учету. В тот момент, когда снаряд вылетает из ствола орудия, пороховые газы начинают также оставлять ствол, причем скорость их становится значительно больше скорости снаряда. Если бы превращение энергии пороховых газов в их живую силу происходило при этом целиком в канале ствола, то определение скорости и не представляло бы затруднений. Ее можно было бы определить из

где А-потенциальная энергия, которою обладают пороховые газы в тот момент, когда снаряд вылетает из ствола, и -кинетическая энергия этих газов в тот момент,

когда они обладают среднею скоростью .

По закону адиабатич. расширения газов работа А определится из ур-ия g а 1

fe-1

Этот закон вполне применим для данного случая, но он не применим во время движения снаряда в стволе орудия потому, что во все это время пороховой заряд лишь постепенно переходит в газообразное состояние, развивая энергию; в тот момент когда снаряд вылетает из ствола, почти весь заряд перешел уже в газообразное состояние, и пороховые газы переходят в такое состояние, когда энтропия их становится величиною постоянною, т. е. когда дальнейшее расширение пороховых газов происходит по закону адиабатич. расширения.

Подставляя в это уравнение адиабат вместо объема а канала ствола выражение I,

где d-калибр орудия и I-длина ствола, и вместо к-1,41, получим:

A = \№qd4[\--:

где q-давление пороховых газов в тот момент, когда снаряд выходит из канала ствола. То обстоятельство, что к концу движения снаряда в стволе незначительная часть порохового заряда еще не превратилась в газ и продолжает переходить в газообразное состояние в то время, когда пороховые газы оставляют канал ствола, оказывает нек-рое влияние на величину А тем, что, понижая коэф. к, увеличивает А. Определить, как велика эта еще не перешедшая в газообразное состояние часть порохового заряда, и вместе с этим учесть влияние этого обстоятельства на величину оказывается пока невозможным, так как на это обстоятельство влияет не только состав пороха, но и вес снаряда и длина ствола, от которых гл. обр. и зависит продолжительность перехода порохового заряда в газообразное состояние, а вместе с тем и б. или м. полное завершение этого процесса. Итак, допустив полный переход потенциальной энергии пороховых газов в кинетическую по закону адиабатич. расширения газов, мы получим:

При F=500 mjck, р = 0,645, g = 350 am, d=7,62 и 1 = 2,3 ж средняя скорость TJ, с к-рой газы оставляют канал ствола, будет равна 1 560 mjck. Подставляя эту величину в ур-ие (2), мы определим отдачу орудия.

Вычисленная т. о. отдача орудия оказывается больше наблюдаемой. Объясняется это тем, что не вся работа А превращается в канале ствола в кинетич. энергию пороховых газов, т. к. газы эти выходят из ствола орудия в виде струи, упругость к-рой значительно выше атмосферного давления. Т.о. только часть работы А превращается в кинетич. энергию пороховых газов в канале ство-

ла и этим влияет на отдачу, увеличивая ее. Решающее влияние на превращение потенциальной энергии газов в кинетическую при истечении их в среду более низкого давления оказывает форма отверстия, через, к-рое происходит это истечение. По законам термодинамики [1], при истечении эластичных жидкостей через обыкновенные цилиндрич. насадки, скорость истечения в конце насадки не может превысить скорости звука, соответствующей состоянию жидкости в насадке, и давление в последней понижается поэтому лишь до давления немного большего половины нача.льного. Более точно зависимость конечного давления от начального выражается ур-ием

Полное превращение давления газа в его скорость происходит только при истечении газа через конич. насадки. Применяя этот закон для данного случая, мы найдем, что при истечении пороховых газов из канала ствола, передний конец к-рого не расширен в виде конуса или борт отверстия к-рого не закруглен, давление этих газов в конце канала ствола понижается лишь до0,53 того давления, к-рое господствует в канале ствола во время истечения. Дальнейшее ионижение давления происходит вне ствола и поэтому не влияет на увеличение интересующей нас Ькорости TJ, а следовательно и на отдачу орудия. Т. о. только 0,47 давления газов в стволе превращается в их скорость внутри ствола. Поэтому и в кинетическую энергию газов внутри стволу превращается только 0,47 А. То обстоятельство, что развитие интересующей нас скорости XJ происходит внутри ствола, нисколько конечно не противоречит тому факту, что наибольшая скорость отдачи соответствует положению снаряда вне ствола, так как самое развитие скорости и происходит в то время, когда снаряд находится вне ствола.

На основании высказанных соображений построено нижеследующее ур-ие, служащее для определения скорости Ь:

Для давлений q в пределах 200-600 aim величина выражения в скобках колеблется в пределах 0,80-0,86. Приняв его равным 0,83 и подставляя вместо sf = 9,81, мы получим:

+ u,mld4.

где и и V-в м/ск, q-в aim, р-в кг, d-в см и I-в м. Ур-ие отдачи принимает т. о. следующий вид:

JP di - f F + ylAeefd4. (2) b

Употребление выведенных ур-ий затрудняется тем обстоятельством, что конечное давление q в канале ствола це во всех случаях известно. Там, где имеются данные относительно этого давления, результаты вычисления отдачи по ф-ле (2) вполне соответствуют действительности. Вычисляя скорость U по выведенной ф-ле для случаев, чаще всего