• Что такое фактурная штукатурка
• Выбираем сухие строительные смеси
• Преимущества напряженного железобетона
• Что влияет на выбор кровельного материала
• В чем преимущество пробковых полов

ные ножи б, которые помещены в особых захватах п при помощи пружин стремятся раздвинуться, так что всегда имеется свободный проход для прокатанной полосы.При поворачивании диска эти ножи двигаются между роликами в, расстояние мелсду которыми устанавливают при посредстве рычага 8 т. о., что ножи доходят один до другого

Фиг. 40.

и далее заходят один за другой. Разрезка происходит в 0,1 ск. После разрезки полоса особой стрелкой д автоматически направляется в различные канавки, так что всякая следующая часть прокатанной полосы находится в другой канавке. Н. приводятся в движение непосредственно от прокатного стана или от отдельного электро-мотора; ножи ножниц должны находиться на уровне пола или рольганга. При холостом ходе Н. потребляют 3-4 ЬР; при разрезывании нагретого круглого железа диам. 15 мм- расход мощности 7 РР, ири разрезывании этого железа в холодном состоянии-9 IP. При проггзводстве по европ. способу кровельного лселеза и жести применяются т. и. дублеры, задачей которых является не только обрезать короткие концы, но и плотно согнуть вдвое раскатанные красные листы. В последнее время появились автоматич. дублеры (фиг. 40), к-рые значительно упрощают работу и об.тегчагот труд рабочего; лист кладется на стол дублера без предварительного сгибания листа, затем лист сгибается поворачивающимися половинами стола, ириче.м средняя часть его удерживается в сгибе особым ножом. По достижении листом настолько сильного загиба, что не имеется опасности выскальзывания его из сгибающих щек, нож быстро отводится кверху, и лист сгибается до соприкосновения обеих половин, подводится под находящиеся с правой стороны дублера П. и обрезается.

Лит.: Браун В., Дыропробивные прессы, нож-ппцы и вальцовочные станки, СПБ, 1908; Тиме И., Справ, книга для горных инж. и техников (с атласом чертежей), 2 изд., СПБ, 1899. В. Щировсний.

НОМЕРАЦИЯ ПРЯЖИ, нумерация иряжи служит для характеристики толщины (или тонины) пряжи. В виду сложности и недостаточности непосредственного замера диаметра пряденой или крученой нити толщина ее определяется взвещиванием и характеризуется или длиной определенного ее весового ко.личества или весом отрезка пряжи определенной длины. Соответственно существует два принципа построения систем номерации пряжи. В первом случае

номер пряжи выражается отношением JV =

а BOBTopoMJVi= где JV-искомый номер

пряжи, JVi-искомый номер, и.ли титр, пряжи, L-длина исследуемого отрезка пряжи, Р-вес исследуемого отрезка пряжи. Первый принцип пололсеи в основу при построении систем Н. и. Д.ЛЯ всех наибо.лее распространенных прядильных материалов (хлопок, шерсть, лен и др.), а по второму построены системы номерации, или титрования, иряжи только Д.ЛЯ шелка как натурального, так и искусственного. Т. о. в нервом случае чем нить (прянеа) тоньше, тем выше номер, а во втором-наоборот. Насчитывают около 30 различных систем Н. п., которые применяются в разных странах для различных прядильных материалов. Эти системы различаются между собой гл. обр. мерами веса и длины, к-рыми выражаются величины L и Р из вышеприведенной ф-.лы. Соответственно системы н называются английская, метрическая ИТ. п.

Для хл.-бум. пряжи почти общепринятой является англ. система Н. п. По этой системе за единицу веса принят 1 англ. фн., а за единицу длины 1 моток, или нетинка, длиной в 840 ярдов. Моток состоит из 7 пасм по 80 питок каждая с общей длиной в 120 ярдов.

ат.1. р

где L-длина пряней в мотках по 840 ярдов, Р-вес пряжи в англ. фи. Это значит, что номер пряней по этой системе обозначается чил ом мотков, приходящихся на 1 анг.л. фн., наир. 32 мотка по 840 ярдов пряжи № 32 весят 1 англ. фн. Во французской системе Н. п. для х.л.-бум. пряжи номер обозначается числом мотков по 1 ООО м каждый, приходящихся на 500 й. Для льна, пеньки и джута в СССР принята английская система Н. п., где за единицу длины принята 1 насма = 300 ярдов и за.единицу веса 1 англ. фн. В русской системе Н. п. д.ля льна, пеньки и джута единицей длины служит 1 талька = 12 пасмам = 3 600 ярдам, а единицей веса Vs пуда, так что в окончательном итоге номерация пряжи по этой системе получается тождественной с английской.

Д.ля шерстяной аппаратной или кардной пряжи в СССР ирименяются следующие системы Н. п.: 1) английская, где номер определяется числом мотков по 560 ярдов, приходящихся на 1 англ. фн.; 2) русская, где номер определяется числом мотков по 1 ООО арш., приходящихся на 1 русский фн. Раз-

личие систем Н. п. создает целый ряд неудобств в торговых сношениях между странами, вследствие чего на международных конгрессах в Вене. Брюсселе, Турине и Париже (1873-1878 годы) принята универсальная система Н. п., употребительная для всех прядильных волокон во всех странах,- это метрическая или международная система Н. п. По этой системе номер равен числу мотков по 1 ООО м, приходяшихся на 1 кг; в частности, камвольная пряжа номеруется преимущественно по метрич. системе Н. п. В табл. 1 приведено соотношение различных систем Н. п.

Табл. 1.-Соотношение различных систем номерации пряжи.

Определение номера крученой пряжи основано на тех же принципах, что и д.1тя обычной, но обозначение номеров делается в виде дроби, где в числителе ставится номер одиночной нити, взятой для кручения, а в знаменателе число одиночных нитей в данной

Если скручивается пряжа разных номеров то номер крученой пряжи, если пренебречь усадкой при кручении, получается по ф-ле

1 = 4-J-4-А. 4- Д-J-N JSi JS2 N-3 iV

где N-искомый номер крученой пряжи, Ni, N2, JV3, ..., Nn-номера скручиваемых пряж, т. е. обратный номер крученой пряжи равен сумме обратных номеров одиночных пряж, напр. если скручивается пряжа № 20 и № 30, то

1 1 , 1 50 - т 600 г.

iv-2o + 30 = откуда J = - =12. Системы номерации, или тптрования, щелка, как мы уже указывали, основаны на другом принципе. Здесь титр (номер) представляет собой вес мотка известной длины. При этом как вес, так и длина принимаются в различных мерах и величинах, в связи с чем и существуют разные системы титрования шелка гл. обр. местного значения. Общепринятым является легальный, или новый интернациональный, титр, где за единицу веса принято одно денье (см.), равное 0,05 г, а за единицу длины-моток в 450 л*. В старом интернациональном титре при той же единице веса за единицу длины принят моток в 500 м. Соотношение между различными титрами таково:

Легальный, или интернациональный . . 1

Старый интернациональный....... 1,111

ту1)ецкий............. 0,992

миланскш!............ 1,035

французский........... 0,996

лионский............. 1,046

Важнейшие системы Н. и. и титрования шелка приведены в табл. 2.

Табл. 2.-в а ж н е й ш и е системы номерации пряжи и титрования шелка.

Род материала пряжи

Система Н. п.

Что выражает собой номер пряжи

Сколько м

пряжи №1 приходится на 1 г

Ско.лько 8 весит 1 Л1 пряжи №1

пряже, напр. крученая пряжа № 32/2 обозначает, что скручено 2 нити пряжи № 32.

Определение номера нряжи производится взвешиванием отмеренной определенной дли-

ньт пряжи, для чего служат приборы: 1) пробное мотовило и 2) весы для пряжи. Отмеривание длины производится на мотовиле, периметр которого различен для пряяот разных волокон. Как видно из фиг., мотовило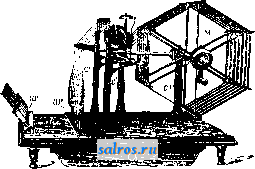

состоит из деревянной подставки, па которой имеется устройство (гнезда или шпинделя) Шх и IZZj Дляс размещения шпуль или початков, с которых разматывается пряжа. На стойках Ci и Cg помещены планки со стеклянными глазками, направляющие нить. Огойка Сз поддерживает мотовило М, которое состоит из шести нар стержней с поперечными пластинками, распстоженных звездообразно вокруг своей оси. Эти поперечные пластинки образуют шестиугольник, периметром к-рого и определяется длина наматываемой нити. Мотовило приводится во вращение с помощью рукоятки через пару конических шестерен на конце своего вала и передает вращение червяку; последний соединен со счетчиком оборотов мотовила. Для хл.-бум. пряжи применяется мотовило с периметром в 1,5 ярда: звонок счетчика отстукивает каждые 80 оборотов этого мотовила, к-рые дают одну пасму в 120 ярдов; по весу ее с помощью вышеуказанной ф-лы обычно и определяется № пряжи. Приборы для взвешивания иряжи, где номер пря-лш получается без всяких вычислений прямым показанием стрелки на шкале,-См. Весы для пряжи.

Лит.: Федоров С А., Об испытании прянш, Определение достоинства прягки и техническая оценка ее как товара, Москва, 1897; Архангельский А. Г., Волокна, прнша, ткани, Москва, 1914; К о-Р о б а н о в А., Насекин Н.и Смирнов К., Крутильное и ниточное производство, Иваново-Воз-иесенск, 1927. А. Великовский.

НОМОГРАФИЯ, совокутюсть метод в графич. построений, выявляющих данные функциональные зависимости иеременнг>1х друг от друга.Совокупность геометрических элементов (отрезков, точек и т. п.), служа-И1ИХ для определения функциональной зависимости переменных, называется номограммой, или абаком. В зависимости <)т того, располагаются ли все элементы номограммы на нек-рой кривой (в частности иа прямой), П.ГГОСКОСТИ или в иросгранстве, номограммы бывают линейные (прямолинейные), илоские и пространственные. По характеру геометрич. элементов, служащих для построения номограммы, последние состоят либо из системы помеченных точек либо из системы помеченных линий; в последнем случае иногда каждой переменной соответствует свое особое семейство кривых

(прямых), совокупность которых образует т. наз. сетку номограммьк Обг^тчно данная ф-ия переменных молсет быть представлена как системой точек, так и системой кривых (прямых), причем между ними сулцествует нек-рое однозначное соответствие. Рассмотрим в качестве примера следующий случай. Пусть имеется ур-ие:

* -f = 1 (1)

1520

В прямоугольных декартовых координатах последнее ур-ие представится графически в виде прямой, отсекающей на оси ж-ов отрезок, равный 15, а на оси у-ов отрезок, равный 20, причем калсдому определенному значению ж, удовлетворяющему (1) и представленному нек-рым помеченным отрезком на оси ж-ов, соответствует нек-рый помеченный отрезок на оси у-ов. Т. о. данньйт график в декартовых координатах представляет собою HOMorpamiy, состоящую иа системы помеченных отрезков прямой. Вместо осей ж-ов и уов можно однако взять дзе параллельные прямые и г/ с нанесенными на них делениями, так чтобы прямая $ соответствовала оси ж-ов, а прямая rj оси у-ов. Тогда точке А на оси у-ов (фиг. 1), имеющей ординату 20 и абсшюсу О, соответствует на фиг. 2 прямая аа, соединяющая деление 20 прямой с делением О прямой f; точно так же точке В, находящейся 1та оси ж-ов (фиг. 1), соответствует прямая ЬЬ фиг. 2. Таким обр. всей прямой АВ фиг. 1 соответствует точка (аЬ) на фиг. 2, получившаяся о г пересечения прямых аа и ЬЬ.Нетрудно видеть, чго точкам, лелсащим на одной и той л:е

{аЬ}

\-10

5 10 15 20 25 Фиг. 1.

Фиг. 2.

прямой фиг. 1, соответствует пучок прямых, проходящих через одну и ту лее точку на фиг. 2, и что пара.ллельным прямым фиг. 1 соответствуют на фнг. 2 точки, расположенные на прямой, пара.лле.льной прямым i и. Г]. Т. о. для .данной системы помеченных отрезков может быть построена соответствующая система помеченных точек, и наоборот.

На практике чаще всего применяются графики, построенные в декартовых координатах, т. е. применяющие систему помеченных отрезков. В технике особенно часто этот способ применяется в тех случаях, когда аналитич. выраясение функциональной зависимости переменных неизвестно,

Am витки Гаусс

а дана лишь экспериментальная зависимость нек-рых частных значений переменных; таким способом вычерчивается напр. кривая намагничивания в электротехнике, кривая JS в термодинамике и т. д. В Н. однако применяются также и другие методы графич. представления функциональной зависимости переменных друг от друга. Так, для ф-ии у = f{x) помимо обычного представления ее в виде кривой в дехсартовых координатах м. б. применен еще и следующий сиоссб графич. изображения. Взяв произвольную прямую X и нанеся на нее в данном масштабе ряд натуральных чисел, получим т. н. натуральную ш к ал у. Отметив затем у каждого деления соответствующее числовое значение переменной у, получим т. н. двойную шка-.л у, к-рая и представляет графически данную функциональную зависимость у от X. При помощи интерполирования можно с достаточной точностью найти значения у и для промежуточных значений ж. В качестве примера приведена на фиг. 3 двойная шка.ла, определяющая зависимость между магнитной индукцией (в гауссах) и числом амиер-витков на см для листового железа. Обычное графич. представление таких зависимостей обладает тем преимуществом, что оно более наглядно, чем двойная шка.ла, но зато последняя, пользуясь только одним вместо двух размеров, занимает меньше места и представляет больше удобств для отсчетов.

2500 2000 1500 1000 \

500 250

25 20

16000

тоо

12000 10000

8000

6000

Фиг. 3.

Фиг. 4.

lo 20 30 V!

Фиг. 5.

50 X

Если имеются две функции одной и той же переменной ху = fi(x) и = /гСж), то аналогичным способом можно построить тройную шкалу. На фиг. 4 приведена например тройная шкала, выражающая взаимозави-

симость давления насыщенного пара воды (в atm), его темп-ры (в °С) и его энтропии (в абс. единицах). Пусть имеется кривая у = /(ж), построенная в декартовых координатах (фиг. 5). Если на оси у-ов нанести деления, соответствующие натуральным значениям X, не нанося значения у, то получится т. н. фун кццональная шкала. Если затем на последней нанести еще и соответствующие значения у, то очевидно получится двойная шкала. Деления обычной логарифмич. линейки представляют собой функциональную шкалу. Модулем, или масштабом, (г(у) функциональной шкалы у = /(ж) называется число единиц длины, (мм или см), содержащихся в отрезке, соответствующем единице переменной у. Наиболее часто встречающиеся и в то же время наиболее важные функциональные шка.лы суть шкалы и от е н ц и а л ь н ы е, логарифмические и проективные. Потенциальную функциональную шкалу, представляющую функциональную зависимость у = х'\ где п-це-.лое или дробное число, можно построить, либо пользуясь графич. построениями в декартовых координатах с логарифмич. делениями (см. Логарифмические диаграммы) либо при помощи таблиц и непосредственных подсчетов. Логарифмич. функциональная шкала, особенно часто применяемая на практике, представляет собой функциональную зависимость y=\gx. На фиг. 6 представлена .логарифмич. функциопальная шкала с модулем /л(у) = 40 мм. Построение проективных функциональных шкал основывается на следую- ф^, q щих началах. Пусть имеются на прямой di точки 1, Bi, Cj, Di и на прямой d, точки J-2, Бз, Сг, Dz, причем пусть имеет место равенство

AiCi . AiDi AzCz . AjDj /рч

BiCi jBiDi Bid B2D2

Обусловливаемая этим равенством зависимость точек называется проективной. Графически проективная зависимость м. б. получена следующим образом. Передвинем совокупность точек А^, В^, С^, Dj по d и совокупность точек А^, В^, С^, по d до совпадения точек J-i и Да с точкой пересечения прямых dx и Взяв затем произвольную точку Р, называемую центром перспективы, нетрудно усмотреть, что прямые PBi, PCi,PDj пересекут при их продолжении прямую 2 как раз в точках В^, С^, Dg, удовлетворяющих соотношению (2).

Если на прямой d взять начало отсчета Ol и обозначать отрезки О^А-, OiBi, OjCi,... через У1, У2, Уя..- и аналогичные расстояния от какого-либо начала Оз на оси d обозначать через Zx, z, z,..., то меледу соответствующими расстояниями у ж z существует соотношение:

, mz + n

где 7с, р, т, п суть нек-рые постоянные. Отсюда следует, что если на прямой d нанести функциональную шкалу z = f(x) и

20 Hits

I Ъ

9 S 7

г

1.Ь

спроектировать ее из какого-либо центра на прямую di, то получится функциональная шкала для ф-ии:

fe/(x)-p. (4)

Рассмотрим в качестве примера построение функциональной шкалы для ф-ииj

в пределах изменения х от 20 до 30. Взяв ось ж-ов, нанесем на нее деления с модулем /.(ж)==10 мм от 20 до 30 (фиг. 7). Возьмем

гЦ ?п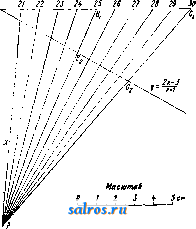

фиг. 7,

на этой же оси две произвольные точки, наир. В, (25) и Ci (30), и найдем подсетом из (5) соответствующие значения для у, а именно Вз (1,808) и С, (1,839). Значению же Ах (20) соответствует значение А^ (1,762). Таким образом отрезку А^В^ на оси ж-ов соответствует Отрезок 1,808-1,762 = 0.046 на оси 2/-0в, отрезку АхС^ соответствует отрезок 1,839-1,762= 0,077. Проведем через А^ прямую у и от-

г лежим на ней в определенном масштабе точки В2,Са,оиределен-ные вышеуномя-нутьв1и величинами. В данном случае удобно взять масштаб Мг/)=1000. Тог-,4 да J.iB2 = 1000x Х0.046 = 46 мм и iC2= 1000x х0,077 = 77 мм. Проведя прямые BiBa и Cia ДО их взаимного пересечения, получим центр перспективы Р. Соединив затем Фиг. 8а. Р со всеми деле-

ниями оси ж-ов и найдя пересечения этих прямых с осью 3/-0в, получим на последней искомую функциональную щкалу.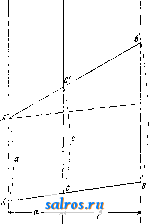

Для номографич. представления ф-ии не-ско.тьких переменных применяются часто несколько параллельных функциональных шкал в зависимости от числа переменных. Пусть имеется ф-ия

2 = mж-fn2/. (6)

Пусть далее имеются три параллельные прямые dx, dz, dg, которые пересекаются двумя прямыми АВ и А'В' (фиг. 8а), из к-рых первую буд'м считать неподвижною, а вторую меняющею свое пололсение. Если обозначить расстояние между dx и d через а, а расстояние между и da через , то имеем:

Ь-с с-а у^мч

/8 ~ а

где а = АА; Ь = ВВ; с=СС. Из равенства (7) имеем далее

а (& - с) = j5 (с - а) или

(а + Р)с^Ра + аЬ. (8)

Если провести вместо А'С какую-нибудь другую прямую, то она отсечет на прямых dx, di, d отрезки, удовлетворяющие равенству (80- Далее, сравнивая равенство (8) с равенством (6), видим, что х vl у играют роль о и Ь, а m и п роль j8 и а. Если положить

z = (m + n)z, (9)

то получим равенство

(т -Ь n)z = тж -Ь пу, (10)

вполне аналогичное равенству (8), или, разделив на некоторую произвольную величи-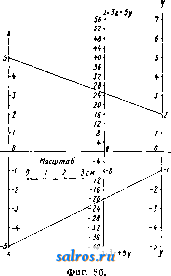

ну I, опрсделяюи1;ую величину масштаба, найдем:

- i- 2 = у a; 4- j у. (И)

Т, о. для построения номограммы, соответствующей равенству (6) или (10), проведем три парал.лельные прямые dx, d, d, так

чтобы расстояние от до d равнялось 1, а расстояние между и равнялось . На

прямой dg можно отложить как шкалу для переменной г', так и шкалу для переменной Z. Т. к. при ж = О, ?/ = О и г' = О, то все три нулевые точки будут лежать на одной секущей прямой; точно так же и деления 3 будут лежать на одной прямой, т. к. при ж = 1, = 1 и z = \.. Что касается переменной Z, то так как при z = 1, Z = т -\- п, делению шкалы Z соответствует деление т + п шкалы Z. Таким образом масштаб для Z в т -\- п раз меньше масштаба для z.

Для примера построим номограмму для функции 2 = Зж -f 5у. Положив 2 = 82 и г = ОД,имеем 80= = 30ж-Ь50г/. Расстояние между осями di и изберем равным 50 мм (фиг. 86), а между da и dz равным 30 мм. Модули для шкал X я у берем /<(ж) = /и(у) = 10 мм. Тогда

для Z имеем модуль /г(.г)= = 1,25жж, т. е.

О

прямая, соединяющая деления 1 шкал ж и у, будет пересекать шкалу z в точке, соответствующей делению 8. Нанеся в полученном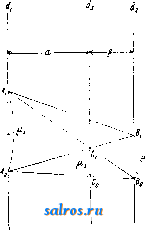

Фиг. 9.

ном итоге сдвинуть вверх или вниз на величину р.

Однако особенньгх практических выгод от применения номограмм,построенных длята-ких простых функций, не имеется. Гораздо большее практическое значение имеют номограммы вышеприведенного типа в соединении с функциональными шкалами. Пусть dy, d, da представляют функциональные шкалы, так что

/2 (у).

/ ,(24.

номограмму

(12) для

;л со Оо Oj

(для расхода S выражен в /сек.)

тогда можно построить следующей ф-ии:

/з() =/1()4-/2(2/), (13).

или, обозначив правую часть последнего равенства через (р (ж, у), ф-ию.

/з() = <р(ж,2/). (14>

Пусть далее мы нашли такие значения Жо, г/о и Xi, 2/1, к-рые дают:

/i(o) =/2(2/0) = 0; /i(Xa) =/2(2/1) = !. Тогда очевидно

?(Жо, 2/1) = /1(Жо) + /2(2/1) = 1; Ч>{Хх, У о) = /i( i) + /2 (2/0)= 1-Нанесем на прямой di точки А„ и Ау, соответствующие значениям Жо и ж а на прямой da точки Бо и By. соответствующие значениям Уд И 2/1 (фиг. 9). Тогда очевидно

yCaJj, 2/о) = ?(Жо, 2/1) = 1 = = CiCo, где -модуль для шкалы d. Кроме того очевидно

ДоА = и БоБх /2 где и - модули для шкал dji dg. Не-§ трудно видеть из фиг. 9

что

(15)

Расход а /сен

(16)

4 5 6 7. 8 9 10

0.02 0.03 ом 005 0.06 0.08 0.1 0. = /сек.

Уклон I

0.001

0,002 0,003 0.04--06 0i

0,01

Фиг. 10.

масштабе на прямой d3 все прочие деления, по.лучим искомую номограмму. (Соединив напр. точку 5 оси ж-ов с точкой 2 оси у-ов, получим в точке пересечения этой прямой со шкалой Z точку 25. Точно так же, соединив точки ж = - 5 и 2/ = -1, получаем на шкале Z точку с делением -20, и т. д. Для ф-ии Z = шх - пу стороны возрастания делений на осях ж-ов и у-ов, в отличие от рассмотренного случая, противоположны. Если имеется функция вида z = тх -\-пу ±р, то построение производят точно также, как и выше, но шкалу z следует в окончатель-

/1 а

При расчете каналов круглого сечения приходится часто иметь дело с

коэфициентом К = г, где

Q - расход жидкости, протекающей по каналу в единицу времени, вы-рал^енный либо в л/ск либо в MicK, а i -уклон. Фиг. 10 представляет номограмму, выражающую зависимости между К, Q и i п построенную на основании вышеприведенных методов, причем шкалы для величин KnQ двойные-в зависимости от двух способов выражения Q (в л/ск и в м^/ск).

Часто применяются также номограммы, у к-рых промежуточная параллельная прямолинейная шкала заменена прямолинейной же шкалой, но пересекающей основные шкалы под некоторым углом. Пересечем две параллельные прямые dj и dg (фиг. 11) прямою da, к-рую будем считать основной прямой, и прямою Z, пересекающей первые две прямые в точках Ах и Ci, а последнюю

прямую в точке Bj. Тогда очевидно имеем: Q-P р а

или р. ,

и u а+с

где AAi а; CCi = с; АВх = р; AC=q. пустим, что шкала - проективная ла от другой шкалы 6, удовлетворяюшей равенству

(18)

(17)

тогда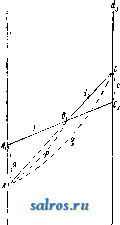

а+с д+1

или а(д + 1) = а + с

с=ад. (19)

Если a=fi(xy, д = и(уу, с = /з(г;), то имеем:

Для оиределения на da шкалы для р, так чтобы

д ~ + 1

отложим на от точ- Фиг^

ки С натуральную

шкалу (фиг. 12), и пусть Р' -предварительный центр перспективы; тогда точке С на da соответствует на da точка р = q (т. к, /2(2/) = О При этом). Проведя из Р' прямую PS II ds, ислучим на da точку, к-рая соответствует /2(2/) =оо, т. е. точка S должна обозначать деление р = 0. Отсюда следует, что SC = q, о, т. к. обусловлено, что АС= q, то точки S п А должны совпадать, т. е. центр перспективы должен находиться на di, например в точке Р. Что же касается модулей, то нетрудно доказать, что между ними должно существовать соотношение:

-(/--ШГ- (21)

где h = РА, причем все модули выражены ./ конечно в одних

d, и тех же единицах длины. В качестве примера рассмотрим построение номограммы для функции

з^хУ. (22) Из (22) имеем

]S2 = ylgx (23) и, сравнивая (23) с (20), получаем: U(z) = lgz, h(x) = gx; Ш) = У- (24) Отложим на di деления, которые соответствуют Ig X, причем , пусть jm(/i) = 40 Wy>l лш(фиг. 13). На dg строим натуральную щкалу для f{ij) = ус модулем /л^) = 16 мм (на фиг. обозначения для этих делений взяты в скобках). От точки А, соответствующей делению 1 первой шкалы, отложим отрезок АР h с модулем 8 мм, так что h/x(h) = 8 мм.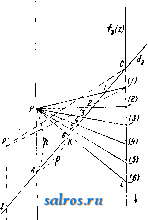

Фиг. 12.

Точку Pi берем в качестве центра перспективы. Проектируя натуральную шкалу у из Pi на da, получим шкалу для р. Затем на dg от точки С откладываем деления лога-рифмич. шкалы fs,(z)B масштабе

К/з) = ~ = 80л1ж,

которые и дадут значения 2, соответствующие тем значениям р и X, которые находятся на прямой, проходящей через все три, частные значения. На фиг. 14а и 146 приведены в качестве примера номограммы для водяных паров, пост-роепные по вышеприведенному принципу. Аналогичными же методами построена на фиг. 15 номограмма для следующего случая. Пусть Р'-вес состава движущегося поезда, Р -вес паровоза, Р=Р' + Р -вес всего поезда, ъ-уклон пути (тангенс уг.ла наклона), Е-сила тяги паровоза, R и R -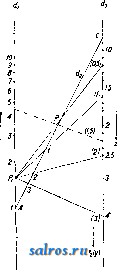

фиг. 13.

S 700 \

650 \

40 \ 250°

35Г

-220°

0.08

0.09

0.10

0.11

1.00 1.50

Фиг. 14 a.

сопротивления передвижению на единицу веса состава и паровоза. Тогда имеем

F = Р' (Д' -1- г) -f P {R + г). (25)

Для данного поезда Р -величина постоянная, а F, R я R -переменные, зависящие от скорости V поезда определенным, устанавливаемым эмпирически, образом, так что 150

650 ]

10 [130°

110° 100° 90°

70°

60°

50°

20°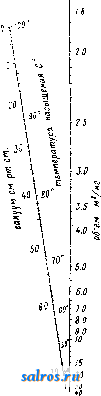

Фиг. 146.

ур-ие (25) связывает между собою величины Р , V, г. Из ур-ия (25) имеем, обозначая F - I>\R - R) F\v) и = 0(v),

(26) F\v) и

F(v) = P[0iv) + i]. Установив эмпиретески функции Ф(ь), можно построить номограмму для (26), выражающую зависимость между Р, V н i. Номограмма построена на основании опреде- ленных эмпирических данных, при. весе паровоза,ра-, в ном 25 т.

Часто применяют номограммы с тремя прямолинейными шкалами, пересекающимися в одной точке. Последнего тина номограммы

применяются для графического изображения функций следующего вида: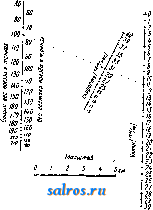

Фиг. 15.

с

/2(У)

(27)

Во многих случаях является более пе.чесо-образным применять криволинейные шкалы вместо прямолинейных. Пусть имеются три кривые di, d-i, d, ур-ия к-рых в декартовой системе осей координат , т] будут:

V=ФШ П-Фт\ ? = Фз(). (28) Пусть имеются на кривых точки Pi(fi, %); Pada- a); -Рз(з' ?з), лежащие на одной прямой (фиг. 16). Тогда имеем аналитич. условие для этого:

?i(l2 - з) + 2(3 - 11) + >?3(li - I2) = 0. (29) Представим ур-ия (28) в параметрическом виде:

(di) ... п-Ш); г = ад )

(2) ... n-Uy)\ (30)

(з) ... S = F,iz) J

Подставляя последние ур-ия в условие (29), имеем:

fi(F2 - Fz)+f2(Fz - Fx) + U(Fx - i2) = О, (31) причем левая часть последнего равенства есть некотораяф-ия 9?(ж, у, г). Так. обр.,если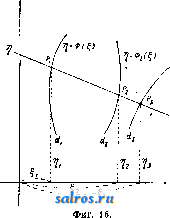

имеется ф-ия трех переменных х, у; z, к-рую можно привести к виду (31),то можно построить номограмму для этой ф-ии таким обр., чтобы соответствующие частные значения переменных х,у, z можно было отсчитывать на сечении прямою всех 3 кривых номограммы.

Лит.: в пол Л. С, Графич. методы техиич. расчетов(номография), Харьков, 1929;Пир а п и М., Методы графич. изобран5е.ний в науке и технике, Берлин-Рига, 1923;L а с m а п п 0., Die Herstellung gezeichneterReclien tafeln, Berlin, 1923; Luc key p., Einliihrung in die Nomographie, T. 1-2, Lpz. u. В., 1918-20; P i r a n 1 M., Die graphische Darstellung in Wissenschaft u. Tecbnik, В., 1922; S с h m i d t Tli . Darstellende Oeometrie, 2 Aufl., B. 2, Berlin, 1923; Schwerdt H., Lehrbuch d. Nomographie, В., 1924; Werkmeister P., Das Entwerfen von graphischen Rechentafeln, В., 1923; см. также Логарифмические диаграммы. М. Серебренников.

НОНИУС, см. Верньер.

НОРИЯ, непрерывнодействующее подъемное приспособление, состоящее из ряда черпаков, сидящих на бесконечной цепи. Нория широко применяется в качестве водоподъемного механизма (см.), а также в форме чернакового элеватора (см.) или конвейера (см.) во внутризаводском транспорте. Интересной разновидностью Н. яв.ляЮтся муль-тицеллюлярные цепные насосы (адгезионные насосы), отличающиеся необычайной

простотой устройства: насос состоит из помещающегося в кожухе а (фиг. 1) верхнего шкива б, через который перекинута цепь в, нагруженная снизу тяжелым свободно вращающимся диском г. Верхний шкив приводится в быстрое движение, причем поднимающийся конец цепи захватывает некоторое количество удерживаемой капиллярностью воды, которая выбрызгивается из цепи при проходе ее через верхний блок под действием развивающейся центробежной силы. Форма цепи оказывает значительное влияние на производительность и на кпд всей машины. В наиболее простом виде цепь может быть заменена толстым пористым канатом, обычно же она делается из оцинкованного леелеза и и.меет форму, которая обеспечивает пай-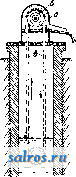

Фиг. 1.

Фиг. 2.

большую поверхность прилипания и возможно большое количество тонких клиновидных углублений, задерживающих воду в силу капиллярности.Распространенным типом является цепь, изображенная на фиг. 2, А, состоящая из обыкновенной цепи, окруженной одним или двумя рядами проволочных спиралей; иногда цепь де.тается из загнутой особым образом полосы железной жести (фиг. 2, Б). Кпд этих насосов довольно низок, особенно ири больших глубинах извлечения воды, что отчасти искупается однако их дешевизной и простотой эксплоатации.

НОРМАЛИЗАЦИЯ И НОРМЫ, см. Стандартизация.

НОРМАЛЬНЫЕ МЕРЫ, см. Эталоны.

НОРМАЛЬНЫЕ РАСТВОРЫ, растворы, со-.цержащие в 1.1 1 граммэквивалент растворенного вещества. Концентрация раствора С-, выраженная в долях концентрации Н. р., принятой за 1 Q-liN), называется нормальностью раствора; прис = 0,Ш (или /loN) имеем децинормальный раствор, при о =0,0Ш (или УюоЮ - сантинормаль-ный и т. д. Концентрации Н. р. меньше концентраций соответствующих им м о л я р-ных растворов (обозначение - моль/л или М) в число раз, равное основности растворенного вещества (например валентности образующих его ионов); так, концентрация /t N раствора двуосновных кислот или щелочей [H2SO4, Ва(0Н)2 и т. д.] равна У^М; для одноосновных соединений (HCl,NaOH) имеем /NlМ. Н.р. (а также молярные) применяются ири очень многих химических и физико-химич. работах, главным образом в химическом анализе (см. Анализ химический), Tji.e пользование ими чрезвычайно облегчает расчеты, т. к. количества веществ, нацело вступающих в реакцию, содержатся в равных объемах Н. р. При изготовлении Н. р, для аналитических

г. Э. т. XIV.

определений, основанных на реакциях оки-счения и восстановления (оксидиметрия, иодометрия), исходят не из обычных грамм-эквивалентов, а из окислительного грамм-эквивалента (количество вещества в г, дающее 1 г-экв. кислорода, идущего на окисление). Чтобы приготовить точный (основной) Н. р., служащий для титрования, отвешивают требуемое количество вещества и растворяют его в мерной колбе, доводя объем раствора до метки ири темп-ре,указанной на колбе (обычно 15°), или вводя, если нужно, поправку на изменение объема колбы с t°. Для приготовления таких растворов берут обычно кристаллические вещества высокой чистоты, негигроскопические и не меняющие своего состава при хранении (наир. от выветривания кристаллизационной воды), янтарную или щавелевую кислоты для алкалиметрии, буру или соду-для ацидиметрии, азотнокисчое серебро, кристаллич. иод и др. Все другие Н. р. (соляной и серной кислот, едких щелочей) изготовляются приближенно, и их точную концентрацию определяют титрованием по основному раствору, после чего объем раствора прибавлением воды доводят до требуемой нормальности(1JV, 0,1, 0,0Ш и т. д.) или вычисляют поправочный коэфициент /, на который надо умножить соответствующую округленную нормальность для получения истинной концентрации раствора. Для быстрого и удобного приготовления Н. р. в продажу выпускаются ампу.лы с запаянной в них навеской твердого или же растворенного вещества, которая при разведении до 1 л дает точно 0,1.? раствор (ф иксаналы фирмы de Наеп). Рационально однако ампулы применять только для таких веществ, для к-рых не молсет быгь взята точная навеска (не для основных Н. р.).

Лит.: Ш и л о в Н. А., Объемный анализ, 3 изд., М.-Л., 1929; Тредвелл Ф., Курс ана.11итической химии, т. 2, Количественный анализ, 2 изд., М.-Д., 1927; К о 1 t h О f f J. М., Die Massanalyse, В. 1-2, В., 1927-28. П. Рвбиндвр.

НОРМАЛЬНЫЙ ЭЛЕМЕНТВестона,

эталон (образцовая мера) единицы электродвижущей силы-международного вольта. Н. э. Вестона представляет собой обратимый гальванический элемент, имеющий при постоянной Г и давлении устойчивую эдс, и м. б. точно воспроизведен при его изготовлении по определенным,наперед установленным правилам (спецификащта). Следует различать два типа Н. э. Вестона: международный Н. э. и кадмиевый элемент.

Международный Н. э. принят Международной конференцией ио электрич. единицам и эталонам в Лондоне (1908 г.) в качестве менсдународного эталона эдс и должен приготов.ляться сог.ласно снецифи-кации, установленной этой конференцией. Он имеет следующую структуру:*

-[Cd](Hg)[CdS04- /3 H20](C(iS04)[Hg2SOi](Hg) + Согласно сп;щнфикации, в качестве электролита слулсит насыщенный раствор CdSOj с избытком кристаллов CdSOi-VsHzO. Положительный электрод состоит из Hg, а отрицательный-из амальгамы, содержащей 12,5%

* Квадратные скобки обозначают твердый ингредиент, а круглые-жидкий.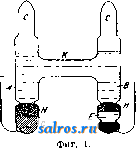

по весу Cd и 87,5% Hg. Деполяризатор, который находится у положительного электрода, представляет собой насту, состоящую из смеси HgjSOi с размельченными кристаллами CdSOi-VsHaO и его водного насыщенного раствора. В качестве оболочки рекомендуется стеклянный сосуд Н-образной формы. Проводники, проходящие через стекло к электродам, должны быть приготовлены из платиновой проволоки, которая не должна касаться электролита. Амальгама помещается в одной ветви элемента, Hg-в другой. Деполяризатор помещается над Hg и в каждую ветвь вводится слой кристаллов CdS04-V8H20. Сосуд наполняется насыщенным раствором CdSOi и герметически запаивается.

Мелэдународные Н. э. приготовляются в главнейщих государственных метрологич. лабораториях раз.чичных стран, в СССР-

в Главной палате мер и весов. Эти лаборатории выработали свои подробные спецификации для приготовления материалов, входящих в состав Н. э., и его наполнения, которыми обеспечивается высокая степень их воспроизводимости, достигающая 0,002 % (эдс различных партий Н. э., приготовленных в разное время согласно этим спецификациям, отличается от партии к партии не более, чем на 2-10 V). На фиг. 1 дано схематич. изображение Н. э., приготовляемых Главной палатой мер и весов. Здесь А-анодная ветвь, В-катодная, обе диаметром ок. 12 мм; D-ртуть, отделенная перетяжкой от остальной части катодной ветви; эта перетяжка затрудняет проникновение Hg в вышележащую часть ветви при опрокидывании или встряхивании элемента, благодаря чему элемент становится устойчивым к условиям перевозки; Е-паста, Л-размельченные кристаллы CdSOi-/gHaO, насыпаемые до второй верхней перетяжки катодной ветви. В анодной ветви: G означает амальгаму, заполняющую нижнюю ее часть, Н-размельченные кристаллы CdSOi-V3H2O, насыпаемые также до сужения в анодной ветви. Насыщенный раствор F сернокислого кадмия нанолняет обе ветви немного выше соединительной трубки К с 0 ~ мм; С-цилиндрич. отростки 0~ % мм, служащие для нанолнения элемента и запаиваемые на высоте ок. 20 мм выше их основания. Платиновые проволочки впаяны в нижние части обеих ветвей и внутри сосуда амальгамированы. Общие размеры элемента: ширина ~ 55 мм, высота ~ 70 мм; общий вес элементов в футляре ~ 650 г.

Кроме Н. э. классич. Н-образной формы в Г.71авной палате мер и весов выработаны и приготовляются Н.э. новой формы с концентрически расположенными ветвями, имеющей перед Н-образной формой известные преимущества в смысле портативности,умень-шения числа спаянных мест у стеклянной оболочки и более благоприятных Г-ных

с-а

условий. Схема элемента этой формы изображена на фиг. 2. Катодная ветвь В 0 он, 11 мм входит внутрь анодной ветви А, имеющей 0 ~24 мм, так что снаружи выступает только ее нижняя часть. Пилиндрич. отросток С0~ 1Ъ мм служит для наполнения элемента, и в целях облегчения наполнения обеих ветвей распололсен несимметрично по отношению к их оси. Буквы D, E,F,

G, Н имеют те же значения, что и на фиг. 1. Общие размеры элемен- Л^, та след.: наибольший ди- с аметр ~ 24 мм, высота до основания отростка С ~ 33 мм, а вместе с отростком ~ 60 мм; общий Фиг. 2. вес элемента в металлическом футляре ~ 260 г, в деревянном ~ 140 г.

Эдс международного П. э. Вестона была установлена в 1910 г. в Вашингтоне особой Технич. комиссией, состоявшей из представителей метрологич. лабораторий Англии, Германии, США и Франции, с точностью до 10 * V: ii;= 1,0183 международного вольта при 20°. Современная точная электрометрия требует уже знания пятого знака после запятой , к-рый определяется путем сравнения с основным эталоном вольта, хранимым в государственных метрологич. лабораториях. Этот пятый знак не одинаков у различных элементов. Одним из главных достоинств

H. э. является его малый °-ный коэф. Для определения эдс нормального элемента нри различных температурах между О и 40° Лондонской конференцией 1908 г. принята следующая формула:

Et = Е20 - 0,0000406(f - 20) --0,00000095 (t - 20)2 + 0,00000001 Ф-ла применима только в том случае, когда обе ветви находятся при одной и той же t°; это объясняется тем, что обе ветви имеют большие температурные коэф-ты, почти одинаковые по величине, действующие на эдс в конечном счете компенсирующе. Внутреннее сонротивление Н. э. колеблется в пределах 500-М ООО Q.

Основным эталоном международного вольта в Главной палате мер и весов служила группа из 20 Н. э.,. приготовленных в 1910 г. В 1922 г. входящие в эту группу элементы были отобраны из числа наиболее устойчивых, сохранившихся к тому времени. Их эдс установлена на основании сравнения с элементами Национальной физической лаборатории в Англии, эдс к-рых была определена по серебряным вольтаметрам (см.) Технич. комиссии 1910 г. в Вашингтоне, а также на основании непосредственных определений их эдс по серебряному вольтаметру в Главной палате в 1910 и 1912 гг. С марта месяца 1929 г. значение международного вольта, определяемое указанной выше группой, перенесено на вторую эталонную группу, образованную в 1928 г. из 20 Н. э., приготовленных в Главной палате в период времени с сентября 1927 г. по апрель 1928 г.; эта группа т. о. и является в настоящее время (1930 г.) хранителем величины междл-народного вольта СССР.

Кроме чисто метрологич. области применения международные Н. э. получили широкое распространение в качестве рабочих эталонов в исследовательских лабораториях, особенно в связи с увеличением применения в лабораторной практике компенсационных приборов для измерения эдс и силы тока.