• Что такое фактурная штукатурка
• Выбираем сухие строительные смеси
• Преимущества напряженного железобетона
• Что влияет на выбор кровельного материала
• В чем преимущество пробковых полов

Нафтолы AS.

Название

Л1-НИТр-

о-нафта-лид

п-анизи-дид

/3-нафта-лид

дианизи-дид

м-хлор-0-толуидид

d :0-толуидид

Формула

N0.,

OCHj

OCH;

H,C.

CO-NH

CO-NH-

толуидид аце- )>-NH CO -CH CO CH3 тоуксусной 1;-;

к-ты /-NH-CO-CHj-CO-CHa

СНз

ром диазотированного амина; между тем при применении S-H. необходимо пропитанные раствором jff-нафтолята ткани предварительно высушить, что помимо лишней операции может вызвать и частичное окисление р-наф-толята и потускнение в силу этого оттенка окраски. Поэтому несмотря на довольно высокую цену нафтолов AS, они успешно конкурируют с /3-нафтолом. 2,3-оксинафтойная ь-ислога получается из /S-нафтола при действии на нафтолят углекислотой. При вза-нмодействии 2,3-оксинафтойной кислоты с аминами в присутствии водоотнимающих веществ (преимущественно треххлористого фосфора) получаются ариламиды кислоты общего состава

или в таутомерией форме

00 C(OH)-NH-Ar

в продажу выпущен ряд нафтолов AS, содержащих различные арильные остатки. Один из них является производным не 2, 3-оксинафтойной кислоты, а ариламидом аце-

тоуксусной кислоты, имеющей ту же 5-дикетонную структуру, что и 2,3-оксинафтойная к-та в таутомерией кето-форме

СНз-С^О

СНа-со-NH-Аг

Нафтолы AS с различными основаниями дают всевозможные оттенки цветов и выпускаются в продажу под общим названием нафтолов AS с добавлением букв, характеризующих их марку. Эти нафтолы AS следующие (см. табл. на сг. 369).

О применении нафтолов AS см. Крашение.

Лит.: Петров П., Викторов П. и Малютин Н., Химич. технология волокнистых веществ, Ив.-Вознесенск, 1928; Шапошников-в. г., Общая техно.логия волокнистых и красящих веществ, М.-Киев, 1926; Ворожцов Н. Н., Основы, синтеза красителей, М.- Л., 1925; его же, Ступени в синтезе красителей, Л., 1926. И. Иоффе.

НАФТОХИНОНЫ, производные нафталина, элементарного состава СюНвОа, к-рые содер-л^ат две карбонильные группы СО. Первый Н. был получен непосредственным окислением нафталина в ледяной уксусной к-те хромовым ангидридом; при окислении о-аминофе-нола был получен другой наф-тохинон, изомерный с первым. Строение обоих пафтохинонов было установлено работами Ли-бермана; последний, исходя из ацетил - а - нафтиламина, получил п-нафтохинон 1,4 (схема I) и, исходя из ацетил-/3-на-фтиламина, получил о-иафто-хинон 1,2(схема II), оказавшиеся идентичными с полученными впервые продуктами:

N0., NH, о

NH-CO-СНз NH-CO-GHs NH

00- -СО-СН:,

-NH.CO-СНз NO.J

Я-г о

Кроме вышеприведенных двух Н. (I) и (1Г) возможны теоретически еще четыре П.:

о

I (пара-) 1,4

о

/\/\

П (орто-) 1,2

П1 (орто-) 2,3

IV (амфи) 2,6

О О

О

V (ака-) 1,5

VI (ката-) 1,7

из к-рых первые три-одноядерные хиноны, а последние-двуядерные. 2,3-Н. досих пор не удалось получить, что находится вероятно в связи с особенностью нафталинового ядра, в котором пололгение 2.3 не является о-положением. Ана-, или 1,5-Н., не удалось получить, т. к. при окислении соответствующего ему 1,5-диоксинафталина получается лишь оксн-производное п-нафтохинона--юг-тон (VII) (см. Красящие вещества естественны е):

л II.

о

но о

Ката-,или 1,7-Н., не был получен, т. к. окисление соответствующего ему 1,7-диоксинаф-талина приводит даже при умеренном окислении к дихинону соответствующего динаф-тила (VIII):

NOH ХО о

Mil.

Таким, обр.в настоящее время известны лишь три Н. 1) W-H а ф т о X и н о н, или 1,4-Н., получаемый окислением 1,4-аминонафтола (из а-нитрозонафтола или а-нафтольных азокрасителей), желтые иглы с 1°пл. 125°, обладающий специфич. хинонньцл запахом, перегоняющийся с водяными парами, легко растворимый в большинстве органических растворителей и мало растворимый в воде. 2) о-Н а фт о X и и о и, или 1,2-Н., получаемый окислением 1,2-аминонафтола (из -ни-трозонафтола или /3-нафтольпых азокрасите-.лей), оранжево-красные кристал.лы, разлагающиеся при 115-120°; без запаха, не перегоняется с водяными парами. 3) А м ф и-н а ф-т о X и н о н, или 2,6-Н., получается при окислении 2,6-диоксинафталина в сухом бензоле мелко измельченной перекисью свинца; оранжевые кристаллы, переходящие в серый цвет при нагревании до 135°; обладает сильно окислительными свойствами.

Практич. применение Н. невелико. Благодаря подвижности кислорода, входящего в карбонильную группу,Н. способны к реакциям конденсации с продуктами, легко отдающими два атома водорода. Так, при взаимодействии с гидрокси.ламином Н. переходят в нафтохиноноксимы, которые идентичны с соответствующими нитрозонафтолами. Именно 1,4-нафтохиноноксим идентичен с а-ни-трозон?фтолом, а 1,2-нафтохиноноксим, в зависимости от положения оксимной группы, соответствует либо /8-нитрозо-а-нафтолу либо а-нитрозо-Д-нафтолу.

NOH-i / n-NO

о он

ХОИ n0

Эти нафтохиноноксимы играют большую роль в производстве красящих веществ (см.) и являются либо протравными красителяр/,и либо промежуточными продуктами для приготовления красителей. Получаются они преимущественно нитрозированием а- и fi-нафтолов (см. Промежуточные продукты в синтезе красителей). При конденсации Н. с гидразинами ароматич. ряда получаются нафтохинонгидразоны, являющиеся таутомерами азокрасителей. Так, из 1,4-Н. с ароматич. гидразином получается нафто-хинонгидразон, идентичный с азокрасите-лем, полученным из соответствующего гидразину диазосоединения и а-нафтола но следующим схемам: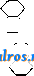

о < ) 0-h3n-NH-RH..0 + 0 у NNH-R:

ОН-< >+CI.N:NIl->HCI-bOH-\-N:N-Il

/ \ / \

При конденсации Н. с производными индоксила в кето-форме получаются красители, имеющие типичную группировку либо инди-гоидов (см. Индигоидные красящие вещества) либо ИНДО.ЛИГНОНОВ (см. Красящие вещес^пва синтетические):

О О

-О

+ СПа

Н.О

о+си,..

О

С

О

т о

NH- О

н.,о

-NH-

Практич. значение имеют оксипроизводные Н. (в частности вышенриведенный юглон) и диоксипроизводные (ценный протравный кра -сите.ль нафтазарин); см. Красящие вещества синтетические - нафтохи ионные красители.

Лит.: Ворожцов Н. Н., Ступени в синтезе красителей, Ленинград, 1926; М е у е г V. и. J а с о Ь-S о п Р., Lehrbuch d. organisclien Chemie, В. 2, Т. 2, Berlin, 192.3. , И. Иоффе.

НАЧЕРТАТЕЛЬНАЯ ГЕ0МЕРИЯ, наука о методах изображения на плоскости пространственных фигур. Методы эти должны дать такое изображение фигуры, при к-рОм по чертежу можно было бы судить об истин-

ной форме и размерах ее и которое было бы наиболее наглядным, т. е. при известной привычке производило бы на нас впечатление пространственного, а не плоского образа. Для целей геодезии, технич. черчения а картографии б. ч. вполне достаточно удовлетворить первому требованию. Для архитектора и художника второе требование является более существенным. Соответственно этому в нервом случае чаще употребляются теоретически более простые, но не всегда дающие наглядный рисунок методы-о р т о-гона.льной проекции на одну и.ли несколько п.лоскостей, во втором случае- метод наиболее близкий к процессу че.ловеч. зрения - центральное проектирование, или перспектива. Простейшие изображаемые нами предметы ограничены плоскими гранями; эти грани ограничены прямолинейными контурами; важнейшие, бросающиеся в глаза, точки--вершины этих контуров, т. е. точки пересечения нескольких прямых .линий.

Естественно поставить требование, чтобы при изображении таких фигур прямые .линии изображались прямыми, а вершины переходили в вершины. Раз.личпрле грани фигуры мы изображаем на одной и той же н.лос-кости-плоскости чертежа, т. е. производим отображение одной лежащей в трехмерном пространстве плоскости на другую. Наиболее

фиг. 1.

-общее преобразование одной шлоскости в другую, при котором прямые переходят в прямые, а вершины в вершины, есть проективное преобразование, или к о .л л и-н е а ц и я, двух плоскостей. Все употребляемые в Н. г. преобразования суть частные случаи наиболее общих проективных преобразований, учение о которых состав.ляет содержание проективной геометрии <см. Геометрия). Эти ж;е методы годятся и при изображении предметов, не имеющих плоских граней,и прямолинейных критуров, наир. кривых линий и поверхностей; но при этом следует помнить, что только прямсли-нейные контуры сохраняют свою прямолинейную форму; форма криво.линейного контура, вообще говоря, меняется. .

1. Центральная проекция, и.ли перспектива. Преобразование перспективы есть проектирование фигуры из нек-рой точки-центра перспективы-с вязкой лучей (т. е. совокупностью лучей, проходящих в пространстве через центр). Перспективным образом точки X предмета является на п.лоскости Т (фиг. 1) точка X пересечения луча ОХ с плоскостью Т. Перспектива есть именно то преобразование, к-рое производит наш

глаз ири наолюдении предмета: лучи зрения, проходя через г.лаз (центр перспективы), переводят все точки предмета в плоскость нашего зрения. Поэтому перспективные чертежи-наибо.лее наглядные, выпуклые, если мы правильно на них смотрим, т. е. совместим глаз с центром О. Опуская из О пер-пендику.ляр на плоскость Т, мы по его основанию II и длине d узнаем расположение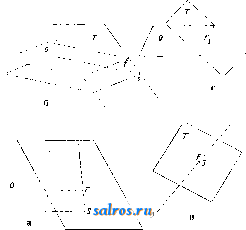

Фиг. 2.

центра. Прямые прп перспективе переходят в прямые, вершины--в вершины. Перспектива есть следовательно преобразование проективное. П.лоскость, вообще говоря, отображается во всю плоскость чертежа. Проективное соответствие, устанавливаемое при этом между плоскостями, называется и е р-с и е к т и в и т е т о м и характеризуется тем. что линия пересечения плоскостей (ось перспективы) сама себе соответствует, так как д.ля точек этой прямой Задача Н. г.

состоит не только в умении отобразить данную пространственную фигуру на плоскости, но и обратно-в том, чтобы по готовому чертелгу определить положение в пространстве изображенных на нем .линий и плоскостей. Ищем поэтому на чертеже те точки прямых и плоскостей, задание которых однозначно определяет их положение в пространстве. Известно, что любая пара точек однозначно определяет прямую, тройка точек или пара параллельных или пересекающихся прямых однозначно определяют плоскость. Для простоты выбираем не произ-во.льные, а вполне определенные точки и .линии (фиг. 2а и 26): 1) след прямой (плоскости), т. е. точку (S (линия s) ее пересечения с плоскостью чертежа, и 2) точку F (.линия/) схождения, определяющую нанрав.ление (положение) нрядюй (плоскости) в пространстве и находящуюся на нере-сечении прямой (п.лоскости), парал,лельной данной прямой (п.лоскости) и проходящей через центр О. Говорят, что точка F (линия /) схождения есть перспективный образ бесконечно удаленной точки (прямой) нашей прямой (плоскости). Линии / и S параллельны между собой. Для прямых (п.лоскостей), проходящих через центр О, точки F и S (.линии / и s) совпадают (фиг. 2в и 2г). Д.ля

прямых п плоскостей, параллельных плоскости чертежа, точки F я S и линии / и s лежат в бесконечности. Во всех случаях кроме последнего точки F я S однозначно определяют прямую, линии / и S-плоскость. Точки пересечения двух прямых переходят в точки пересечения на чертеже. Параллельные прямые переходят не в параллельные на чертеж;е, а в пересекающиеся-Пучок прямых, проходящих через их общую точку схождения F (фиг. 3). Только линии, параллельные между собой и параллельные п.чо-скости чертежа, изобрал^аются параллельными прямыми вследствие того, что их общая точка F лел\ит в бесконечности. Две прямые, не лежащие в одной плоскости, не пересекаются. На чертеже они пересекутся. Если прямые заданы точками Si, Fi, /Sg, Fg, то они пересекаются в пространстве тогда и только тогда, когда линия, соединяющая Si с Sz, параллельна линии, которая соединяет Fi с При помощи задания точек^и S и линий / и S легко решаются задачи пересечения прямой с плоскостью и двух плоскостей. Этими задачами и кончаются вопросы чистой прямолинейной геометрии, не имеющей дела с измерением линий и углов. Задачи измерительного, или метрического, характера, к которым относится и проведение перпендикуляров, перспектива не решает просто,-по следующей причине. При перспективном отображении длины от-])езков и велхшины углов вообще меняются

Фиг. 3.

Фиг. 4. б

И меняются непропорционально. Если отрезок АВ разделен точкой С в отношении

лс т

У^ , ТО при перспективе это отношение

С-В' п) частности середина отрезка переходит не в середину, а в другую точку. Только сложное отношение четырех точек отрезка А, В, С, D. т. е.

ЛВ AD

4С яо сохраняется при перспектрше (фиг. 4а). Для фигур, лел^ащих в плоскостях, параллельно П.ЛОСКОСТИ чертежа, перспектива дает подобные образы, т.е. сохранение углов и сжатие или растяжение длин в определенном отношении (фиг. 46). Сложное отношение хотя и не изменяется при перспективе, однако является слишком громоздким аппаратом для решения простых измеритель-

ных задач Н. г. Проще обратиться к таким методам, где величины изменяются в определенном отношении, т. е. к методу пара,л-лельного проектирования.

2. Параллельная проекци я-частный случай, перспективы, когда центр О удален в бесконечность, т. е. все точки изображаемого предмета проектируются лучами, параллельными пек-рому направлению на п.лоскость чертежа. Изображение получается при этом такое, как если бы мы смотрели иа предмет из очень большого удаления. Выпуклость чертежа сравнительно с перспективой теряется, но зато законы отображения более просты. На законах параллельной проекции основано построение падающих теней. Действительно, источник света-солнце-находится от земли на столь, большом расстоянии, что практически лучи света можно считать параллельными (если источник света находится на небольшом расстоянии от предмета, тень строится по законам перспективы). Прямые изображаются в параллельной проекции прямыми, кроме тех, к-рые параллельны направлению проекционных лучей и следовательно изображаются точкой. Пара.л.ле.льные прямые переходят в параллельные на чертеже. Плоскость ото-бралсается на всю плоскость чертежа. Проективное соответствие, получающееся при этом между плоскостями, назьшают аффинным или аффинитете м; оно характеризуется тем ,что кроме линии пересечения плоскостей к-рая сама себе со-

ответствует по точкам, бесконечно удаленная прямаяодной плоскости переходит в бесконечно удаленную прямую другой плоскости (т. к. параллельные переходят в параллельные). Фиг. о. Это обстоятельство

представляет удобство сравнительно с перспективой. Но с другой стороны, в перспективе образы бесконечно удаленных элементов, т. е. точки и линии схояодения, вместе со следами однозначно определяли поло-Лгсние прямых и плоскостей в пространстве, здесь же образы бесконечно удаленных элементов также лежат в бесконечности и немогут оказать помощи при решении этой задачи. Зато метрич. соотношения в парал-.лельной проекции проще. Длины отрезков; на данной прямой изменяются в одном и том же отпошенип, т. е.

АС А'С^ СВ ~ С'В'

в частности середина отрезка переходит в середину. Длина проекции зависит лишь от направления прямой и нанравления проекционных .лучей, а именно (фиг. 5):

АВ sin а А'В' ~ Sin {а + Й

Следует помнить, что для разных прямых угол /3 меняется, так что в разных направлениях длины изменяются в разных отношениях. Конгруентность, т. е. сохранение всех размеров фигуры, получается (как подобне в случае перспективы) для фигур, которые лелгат в п.лоскостях, параллельных

плоскости чертежа, и только для них. Этим обстоятельством пользуются при выборе плоскости чертежа, к-рый находится в нашем распоряжении в каждой конкретной задаче, а именно выбирают ее параллельною той из граней фигуры, размеры к-рой мы хотим получить истинными, неискаженными. Истинные размеры других граней исследуются методом совмещения их с плоскостью,парал-. лельною плоскости чертежа. Важным частным случаем нараллельн. проекции является т. и. военная перспектива , т. е. параллельная проекция под углом в 45° (а = 45°) к плоскости чертежа, выбранной горизонтально. В этой проекции основания фигур, как параллельные плоскости чертежа, изобразятся без искажения. Кроме того не исказлтся длины высот (фиг. 6): а = 45°; Д=90°;

А^В sin 45°

А'В' ~ sin 135° ~ Часто употребляется таклсе пара.ллельная проекция на вертикальную плоскость под

углом 30°, 45° и 60° (фш. 7). Косая параллельная проекция благодаря возможности выбора угла а и n.TjocKocTn проекции дает чертежи, хотя и худшие, чем перспектива, но все-таки достаточно наглядные. Если отказаться от последнего требования, то простейшей по своим законам и наиболее щль способленной для решения метрич. задач является прямая параллельная, или ортогональная, проекция.

3. Ортогональная проекци я- частный случай параллельной, под уг.лом а = 90° к плоскости чертежа, к-рую как правило выбираем либо вертикальной либо горизонтальной . Длина проекции особенно просто выражается через длину проектируемого отрезка: А'В' =АВ cos р, где /?-уго.л между прямой и плоскостью чертежа. Все точки, лежащие на одном перпендикуляре к плоскости чертенса, имеют одну и ту же проекцию. Определить однозначно по данной проекции форму и размеры фигуры яв.ляется невозможным. Поэтому либо д. б. даны по крайней мере две проекции фигуры, .либо чертеж в ортогональной ироекции должен содержать отметки о высотах каждой вершины по отношению к п.лоскости чертежа. Если плоскость Т-горизонтальна, то высоты над нею считают положительными, а под нею-отрицате.льньпип; если Т-вертикальна, то высоты точек, лежащих перед нею, считают положительными, за нею-отрицательными. Т. о. в каждой вершине проекции прямолинейной фигуры до.лжно стоять некоторое положительное или отрицательное число. Высоты остальных точек находим, сое-

диняя вершины прямыми. Если фигура не прямолинейная, то нужно знать высоту каждой точки. Принципом отметок (топографич. метод) пользуются при черчении карт. Чтобы изобразить рельеф местности, точки, лежащие на одной и той же высоте, соединякл*

0

Фиг^ 8.

Фиг. 9.

.ЛПНИЯЛП1 (т. паз. горизонтали, и.ли .л пн и и у р о в и я), к-рые затем отмечают чис-.лами (фиг. 8). Однако для многих целей значительно удобнее принципа отметок является проекция на две различные плоскости.

4. Ортогональная проекция на две плоскости изобретена создателем Н. г., франц. геометром Монжем (Monge) в 1798 г. За плоскости проекции берем горизонтальную плоскость и вертикальную, выбор к-рой каждый раз диктуется условиями задачи. При чертежах заданий получается т. о. п.лан и фасад здания. Вместо двух отдельных проекций фигуры Монж предложи.л изображать обе проекции в одной и той же п.лоскости след. обр. Вертикальную плоскость вращают вокруг оси проекции (лп-пии пересечения горизонтальной и вертп-ка.льной п.лоскостей) назад до совмещения ее с горизонтальной (фиг. 9). Задняя часть горизонтальной плоскости будет совмещена таким обр. с верхней частью вертикальной, а передняя с ее нижней частью. Точка изображается на двойной плоскости двтмя проекциями, лежащими на одном нериендикуляре к оси проекции а' и а (фиг. 10); при этом расстояние горизонта.льной проекции а' от оси проекции равно высоте точки по отно-п

шению к вертикальной плоскости, расстояние вертикальной проекции а -высоте точки над горизонтальной шлоскостью. В зависимости от того, как расположены проекции точки, над осью или под осью проекции, можно судить, в каком из четырех квадрантов, на которые разбивает наша пара плоскостей пространство, лелотт данная точка (фиг. 10). Д.ля оиределения по.ложения прямой достаточно знать проекции двух ее точек. Соединяя одноименные проекции этих точек пря-лгыми, мы по.лучаем проекции прямой, к-рые вполне определяют ее положение в пространстве. Соответственные проекции двтс параллельных прямых пара.л.ле.льны. Чтобы опре-

делить, пересекаются ли две прямые, мы долл-сны рассмотреть точки пересечения их одноименных проекций. Если эти точки пересечения лежат па одном перпендикуляре к оси проекций, то прямые пересекаются, в противном случае-нет. Плоскость изображается обычно либо проекциями некоторого лежащего на ней тр-ка или мп-ка (в частности параллелограма) либо прощсциями двух лежащих на ней пересекающихся или параллельных прямых. При этом на плоскости особенно ва-

\У жную роль играют

[), 2 семейства линий:

линии параллельные горизонтатьной плоскости, или ЛППИ11 в ы сот, и линии па-ра.ллельные вертикальной плоскости, гпгогда называемые

- .л и пиями ф р о н-

Фиг. 11. та. Линии высот во-

обще пересекаются с линплми фронта; для плоскостей, парал-.ле.льных оси проекции, оба семейства совпадают. Пара линий по одной из каждого семейства определяет плоскость.

Задача пересечения прямой и плоскости. Д.ля нахождения точки пересечения прямой и плоскости (заданной проекциями парал.ле.лограма) проводим че-I )ез прямую вспомогательную плоскость, перпендикулярную к горизонталыюй п.лоскости проекции. Горизонтальная проекция вспомот зательной плоскости совпадает с горизонтальной проекцией А'В' нашей прямой (фиг. Л). Ищем проекции точек х, у пересечения вспомогательной плоскости с двумя из ребер паралле.лограма. Горизонтальные проекции ж', у' этих точек найдутся на пересечении А'В' с горизонтальной проекцией параллелограма, вертикальные проекции ж , у -на пересечении перпендикуляров к оси проекции их х', у' с вертикальными проекциями этих ребер. Соединяя ж су пунктирной vTHHHeE, мы на пересечении ее с вертикальной проекцией А В нашей прямой найдем вертикальную проекцию s искомой точки S пересечения прямой и плоскости. Д.ля нахождения горизонтальной проекции s достаточно провести перпендикуляр из s к оси Цроекции, до встречи его сАВ'. Ясно, что построение можно вести, использовав другую вспомогательную плоскость, перпендикулярную к вертикальной плоскости проекции. Результаты обоих построений должны Ьовпасть, на чем и основан снособ проверки.. Задача пересечения двух плоскостей сводится к предыдущей. Ищем точки пересечения одной из плоскостей с двумя прямыми другой плоскости и соединяем полученные точки прямой линией. Задача проведения перпендикуляра к данной плоскости. Ни перспектива, ни косая параллельная, ни даже ортогональная проекция не сохраняют величины углов, а следовательно и свойства перпендикулярности. Прямой угол изображается в ортогональной проекции как прямой тогда и только тогда, когда одна из его сторон парал.лельна п.лоскости проекции.

Если плоскость задана проекциями линий высот и линий фронта, то перпендикуляр к п.лоскости (а следовательно и к обеим этим линиям) будет иметь горизонтальную проекцию перпендикулярною к горизонтальной проекции линии высот и вертикальную проекцию перпендикулярною к вертикальной проекции линии фронта. Отсюда простое построение перпендику.ляра к плоскости (фиг. 12). То же построение в обратном порядке слулшт для проведения плоскости перпендикулярной к данной прямой. В этом построении и состоит главное преимущество ортогональной проекции перед любой косоугольной проекцией.

Переходя к задачам метрическим, мы встречаемся здесь прежде всего с опреде-.лением истинной величины отрезка. Если уго.л а наклона отрезка к п.лоскости проекции задан, то величину молуно вычислить по

ф-ле АВ = . Но обычно величина угла а

cos а

неизвестна, заданы .лишь проекции отрезка. Поэтому важно иметь геометрич. конструкцию, дающую истинную величину отрезка.

Задача определения истинной длины отрезка. Проекции отрезка АВ меньше истиппой величины его, кроме случая параллелизма отрезка и одной из плоскостей проекций. Чтобы привести отрезок в такое по.ложение параллелизма, его вращают вокруг нек-рой оси, к-рую выбирают парал-.лельною п.лоскости проекции. Осью вращения может служить например проходящая через В линия высот h той вспомогательной п.лоскости, которая проходит через АВ и перпендикулярна горизонтальной плоскости проекции. Горизонтальная проекция W линии h (фиг, 13) совпадает с горизонтальной проекцией А'В' нагнего отрезка, вертикаль-

Фиг. 12.

Фиг. 13.

нал проекции h параллельна оси проекции. Вспомогательную плоскость вращаем вокруг h до тех пор, пока она попадет в положение, параллельное горизонтальной плоскости. Горизонтальная проекция (А') точки J. в новом положении будет лежать, как-легко видеть, на перпендикуляре к В'А' в точке А', на расстоянии А'(А'), равном расстоянию от точки А до h . Пунктирная линия В'{А') дает истинную величину АВ.

5. Ортогональная аксономет-р и я-ортогональная проекция на три взаимно перпендикулярные плоскости. Точка, как-известно из метода координат (см,), вполне определяется такими тремя проекциями. Для изображения всех трех проекций на одной и той же п.лоскости чертежа проектируют их вместе с осями координат на эту пло-

НАЧЕС

скость косоугольно. По теореме Польке, любая тройка отрезков на плоскости ОХ, 0Y, 0Z таких, что не все четыре точки О, X, Y, Z лежат на одной прямой, есть нек-рая косоугольная проекция трех единичных (длины 1) отрезков осей прямоугольных координат в пространстве. Поэтому тройку отрезков, координатный триэдр, можем выбрать произвольно, под любыми уг.тами и .тюбой длины. После этого изображение фигуры производится так, как это делается в нна;и1тич. геометрии, т. е. по координатам точе1с. Выбор координатного триэдра дает

У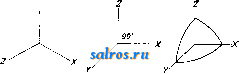

Фиг. 14.

нам относительную единицу масштаба на каждой из осей, так что и обратно-по данным проекциям молсем определить координаты точки. Выбор триэдра дает кроме того перпендикулярные направления на калодой пз координатных плоскостей, что представляет большие удобства при построении перпендикуляров . Аксонометрия дает при весьма простых средствах наглядные чертежи, поэтому нри всех рабочих чертежах именно 1ша и употреб.ляется. На фиг. 14 даны наиболее употребительные триэдры и аксоно-метрич. изобраншпие поверхности шарового сектора.

Круг и конические сечения. При перспективе любое конич. сечение может перейти в любое другое. В этом можно убедиться, помещая центр перспективы в вершину конуса (см. Конические сечения, фиг. 1). При параллельной проекции конич. сечения переходят в одноименные. Действительно, строя на данной кривой цилиндр (косой или прямой), всякую проекцию ее мы получим как сечение цилиндра нек-рой и.ло-<КОСТЬЮ, непараллельной образующим ци-.ппщра (фиг. 15-эллиитич. цилиндр). В частности параллельная проекция круга есть

Фиг. 15.

фиг. 16.

эллипс. Желая получить проекцию сферы (поверхности шара), мы только в сечениях, параллельных плоскости чертежа, можем изображать круги, в других сечениях-эллипсы (фиг. 16). При параллельной проекции сохраняется свойство сопряженности; в частности пара взаимно перпендикулярных диаметров круга переходит в пару сопряженных диаметров эллипса. Н. г. находит применение гл. обр. в техническом черчении.

Лит.: Пальшау А., Начала начертательной геометрии, 9 изд., Москва-Ленинград, 1927; Weber Н. u. Wellstein j., Энцнк.лопедия эле-

ментарной математики, 2 изд., т. 2, кн. 1, Одесса 1913; Salkowski Е., Gruudzuge d. darstellenden (Jeonietrie, Leipzig, 1928; Scheflers G., Grund-7uge der darstellenden Geometrie, 2 Auflage, B. 1-2, BerHn, 1922-27. Ю. Рожанская.

НАЧЕС, см. Ворсовальная машина. Ворсовые ткани и Ткани.

НАШАТЫРНЫЙ СПИРТ, см. Аммиак.

НЕВИЛЬ-ВИНТЕРА КИСЛОТА, а-нафто.т-4-сульфокислота, наиболее ваягная из суль-фокпслот а-нафтола. См. Промежуточные продукты синтеза красителей.

НЕГАДИН в радиотехнике, схема лампового генератора, работающего от двух-сеточиой .лампы, в к-рой колебательный контур включен в общий участок цепей кон-тро.льной сетки и сетки пространственного заряда. В Н. генерация осуществ.ляется при отсутствии какого-либо сиециа.льного устройства обратной связи; катушка колебательного контура является одновременно катушкой обратной связи. В этом заключается одно из преимуществ негадинной схемы. П. впервые предложен был голландцем Ну-маном, почему эта схема иногда называется также схемой Нумана.

Н. находит применение гл. обр. для целей регенеративного приема при двухсеточных .лампах. Телефон при этом включается в

Ц|Н|-Фиг. 1.

-1------

Фт. 2.

анодную цепь. Особенно рационально применение Н. при приеме от рамочной антенны, т. к. он, не требуя специальных устройств для обратной связи, значительно облегчает вопрос об осуществлении регенерации неносредственно в контурах рамочной антен- ны. Степень обратной связи в Н. регу.лирует-ся или изменением накала лампы или изменением при немощи переменного сопротивления напряжения на сетке пространственного заряда. Первый способ дает менее плавное наступление регенерации, чем второй; при этом он проще и в эксплоатационном отношении. Регенерация в Н. обычно резко наступает при малом напряжении накала, следовательно малом анодном токе, затем при дальнейшем повышении нака.ла она держится постоянной и резко обрывается при достижении определенного максимального накала. Для получения плавного наступления регенерации в цепи сетки пространственного заряда должна участвовать .лишь часть катушки колебательного контура (фиг. 1), и в анодную цеиь вк.лючается дроссель (см. схему фиг. 2). На фиг. 3 даны типичные для Н. кривые зависимости анодного тока (в шА), при которол! наступает регенерация, от числа действующих в цепи сетки пространственного заряда витков в % от их общего числа. Кривая / относится к случаю, когда в анодной цепи нет дросселя, кривая II-при включенном дроссе.ле, имеющем L= 0,6-10 см и Д=26,2 , и кривая III - для дросселя, имеющего L = 1,65 10 см и i?= 59 Все кри-

вью относятся к немецкой лампе RE-26. Дроссель в анодной цепи способствует также получению равномерной регенерации на широком диапазоне волн. Негадинная схема применяется и в сверхрегенеративном радиоприеме. В этом случае колебания вспомогательной частоты получаются от контура,

щ

Ю 30 50 10 90 WX Фиг. 3.

Фиг. 4.

настроенного на эту частоту и включенного последовательно с контуром принимаемой частоты также в обшем участке цепей контрольной сетки и сетки иространственного ларяда (см. фиг. 4). Н. находит также применение и в измерительной технике как устойчивый и удобный в работе генератор с одной катушкой.

Лит.: Mittelmann Е., Untersuchungen йЬег die Schwingschaltung, von Numans-Rosenstein, Jalir-buch d. drahtlosen Telegrapliie u. Telephonie , Berlin, 1926, B. 28, H. 6,- M i t t e 1 m a n n E., Weiterer Bei-trag zur Negadynsclialtung, ibid., 1927, B. 30, H. 5; W i g g e H., Rundfunkteclinlscbes Handbuch, B. 1-2, Berlin, 1925-27.

НЕГАТИВ, фотографическое изображение, отрицательное по отношению к снимаемому объекту в смысле распределения светотени: чем ярче освешены отдельные части объекта, тем темнее они выходят на Н. Это объясняется тем, что в большинстве способов фотографич. воспроизведения (примеры и исключения-см. Фотография) действие света, упавшего иа фотографич. материал, заключается в почернении последнего, зависяшем от яркости света. Н. не является конечной целью нри получении фотографич. изображения, которое должно передавать распределение светотени объекта в прямом, а не в обрашенпом виде. Каждый Н. является лишь промежуточной ступенью для получения не-ограниченного числа позитивных изображений с правильной передачей светотени. Позитив получается или путем о б р а ш е-н и я Н., или путем контактного п е ч а т а-п и я, или увеличения с П., или наконец фотографической съемкой П., если последний получен на непрозрачной подложке, напр. фотографической бумаге (см. Бумаги фотографические). Хороший Н. является поэтому необходимым, хотя и недостаточным условием получения хорошего фотографич. изображения, и оценка качеств и свойств Н. является серьезной задачей для каждого ф)Отографа-практика. От правильности этой оценки зависит возможность исправления недостатков П. путем его химической обработки (усиление, ослабление и т. д.), ретуши, подбора бумаги для позитива, способа печатания и т. д. Нормальным называется Н. с правильной передачей светотени объекта. Это значит, что участки объекта, иредстав-ляющиеся глазу наблюдателя одинаково яркими, должны вызвать на П. одинаковые почернения и что почернение иа негативе

должно быть пропорционально яркости объекта. Количественно яркость данного участка объекта определяется интенсивностью испускаемого или отражаемого им света, а почернение на Н.-непрозрачностью данного участка П., т. е. отношением количества падаюшего на него света Jq к пропушен-

ному свету J: непрозрачность 0= ~ Логарифм непрозрачности называется плотностью П.: D=lgO=lg - Для бромосеребряных эмульсий (см.) плотность пропорциональна количеству выделившегося (после проявления) серебра.

Если почернения на Н. нарастают медленнее, чем яркости объекта, то П. назьгеается мягким; если мягкость Н. выражена в такой степени, что природные контрасты сильно смягчены, и негатив является мало пригодным для получения с него позитива, то Н. называется вялы м. Если, наоборот, контрасты освещения объекта передаются слегка преувеличенно, П. .называется к о н-трастным, если сильно преувеличенно-лс е с т к и м. Эти отклонения от нормальной передачи светотени объекта м. б. исправлены в процессе проявления (см.) негатива, поэтому весьма валено, чтобы фотограф уме.л определять характер Н. в темной комнате при слабом свете красного или зеленого фонаря; это умение приобретается длительным опытом. Значительно труднее исправить недостатки светопередачи по выходе из темной комнаты, т. е. по окончании фиксирования (см.). Тогда можно подвергнуть мягкие и вялые негативы усилению, контрастные и жесткие П.-ос л а б л е н и ю. Если весь И. является очень прозрачным, то он называется тонким; если, наоборот, все изображение очень темно (выделилось слишком много металлич. серебра), то П. называется плотным. Тонкие П. также м. б. исправлены усилением, а плотные- ослаблением, но способы химич. обработки здесь иные, чем для исправления ненравиль-ной передачи контрастов освещения. Часто Н. бывает затянут б. и.ли м. плотной вуалью (см.), серой или цветной, к-рая д. б. уда.лена ослаблением и.ли другими способами химич. обработки. Нормальным считается Н. с правильной передачей светотени, лишенный вуа.ли, с достаточной, но не чрезмерной плотностью в светах (темных местах П., соответствующих светлым участкам объекта) и хорошей передачей деталей в тенях (светлых местах Н.).

В целях сохранения оригинального ГЕ, представляющегося особенно ценным или редким, нриготов.ляется его фотографич. копия, т. и. д у б л и к а т П., получаемый обыкновенно при помощи диапозитива (см.). К получению дубликата Н. приходится прибегать в том случае, если первоначальный Н. с редкого или неповторимого сюжета настолько неудачен, что не допускает непосредственного копирования. С него получают диапозитив, а с последнего-дубликат П., и на нем приступают к процессам усиления или ослабления, к-рые могли бы испортить ценный П. Соответственным подбг -ром сортов эму.льсий и способа прояв.ления

можно добиться дубликата Н. с совершенно иной градацией (см. Фотография, Сенситометрия) и т. о. исправить недостатки Н.

Лит.: Фотография и аэрофотография, под ред. Д, Сольского, пер. с нем., Москва, 1926; Э н г л и ш Е., Основы фотографии, М.-Л., 1927; G О 1 ci b е г g Е., Der Aufbau d. photographischen Bildes, Halle a/S., 1925; E d er J. M., Handbuch d. Photographie, T. 2 und 3, Halle a/S., 1903; Hauberrisser G., Wie erlangt man brillante Negative und scheine Negative, 21/25 Aufl., Lpz., 1925; M e u t e, L 6 h m a n u. N a-u с к. Das Negativverfahren, Handbuch der Photo--graphie, hrsg. v. W. Vogel, B. 2, T. 2, Berlin, 1926; 5cheffer, Die Grundlage der Photographie, Ber-Ип, 1917. A. Рабинович.

НЕГАТРОН, иредложенная Скотт-Та]гартом (заявка 1917 года) схема со специальной четырехэлектродной электронной лампой (см. Лампа электронная). Эта негатронная лампа в отличие от обычного триода обладает двумя анодами (фиг. 1): главным и отклоняю-ш;им А 2, причем последний обычно ббльших размеров, чем Ах. С такой лампой осуществляется падающая характеристика тока ia на Л1 относительно напряжения Vg на сетное G (фиг. 2) благодаря тому, что при подхо-

Vg=eO вольт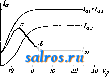

Фнг. 1.

Фиг. 2.

.дящем подборе геометрии, размеров и взаимного расположения сетки и обоих анодов ток lai увеличивается за счет тока /д^. Такая падающая характеристика аЬ (фиг. 2) обусловливает наличие отрицательного сопротивления (см.) < О (отсюда название Н.),

к-рое, как и в вольтовой дуге (см.)или динатроне (см.), способствует возникновению колебаний в колебательном контуре LC (фиг. 1). В этой схеме сетке G сообщается необходимое (мгновенное) напряжение от колебательного контура через конденсатор Ci, причем увеличение напряжения на А^ увеличивает Vg и тем уменьшает li (благодаря увеличению /да)- Утечка через большое сопротивление R обеспечивает, как обычно, поддержание нужного среднего напряжения на сетке, фиксируя тем самым выгодную рабочую точку на характеристике. Д и (7i м. б. в их действии заменены особой батареей, включаемой вместо Сх отрицательным цолюсом к аноду Ах и положительным к сетке G. Рабочая точка и ток нака.ла выбираются так, чтобы полный ток испускания Ji + Iz равнялся току насыщения и распределялся между Ах и J.2 примерно поровну. Технического успеха Н. не имел.

Лит.: S с о t t-T а g g а г t Т., Radio Review*, N. Y., 1921, V. 2, p. 61; Jahrb. d. drahtl. Telegraphie und Telephonic*, ВегИп, 1922, В. 19, p. 148; Taschen-buch d. drahtlosen Telegraphie u. Telephonic, hrsg. v. P. Banneitz, Berlin, 1927; H a b a n n E., Jahrbuch der dKahtl. Telegraphie u. Telephonies, Berlin, 1924, B. 24, H. 5/6; Au. П. 166260/17. Б. Введенский.

НЕЗАТУХАЮЩИЕ КОЛЕБАНИЯ, см. Колебания электрические. НЕИЗМЕНЯЕМОСТЬ ГЕОМЕТРИЧЕСКАЯ,

неизменяемость системы, свойство стержневой системы сохранять свою те-

т. э. т. XIV.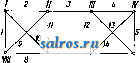

оретическую схему и взаимное расположение отдельных частей в пределах упругих деформаций, вызываемых нагрузками. Стержневые системы с жесткими узлами неизменяемы по существу конструкции своих узлЬв, например жесткая рама (см.); стерж-ш 7 Ml в V невые системы с шарнирн.соедине- НИЯЛ1И узлов, на-

пример фермы (см.), требуют особого определения своей неизменяемости. Всякую систему молшо рассматривать как состоящую из ряда стержней и неизменяемых дисков (см. Система). По условию статической определимости число полных пгарииров S в системе и число п стержней или дисков должно удовлетворять условию п = 2S - 3 (см. Система). Если число стержней ?г < 2*5-3, то

система заведомо а Ij

Фиг. 2.

изменяема. Но и условие п = 25-3 и п > 25* - 3 (система статически неопределима) не гарантируют неизменяемости системы; например показанная на фиг. 1 система, в которой >S = 8 и п = 14, т. е. 14 > 2-8-3, по своему образованию является изменяемой. Простейшими образованиями системы являются соединение двух дисков шарниром и стерншем (фиг. 2а). или, что то Hie, ирисое-

а б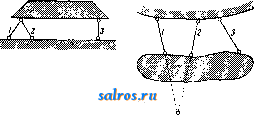

динение узла двумя стержнями (фиг, 26), и соединение двух дисков тремя стерлшями, не пересекающимися в одной точке (фиг. 3 а и б). Последующее развитие системы делается путем присоединения к исходной неизменяемой системе новых дисков, узлов и систем одни.м из указанных выше способов; напр. на фиг. 4 показана комбинированная

Фиг. 4,

система, неизменяемость к-рой можно проследить следующим образом по ее образованию. Фермы 1-2-5-S и S-5-2-1 как образованные из тр-ков представляют собой неизменяемые диски;к ним присоединены узлы б, 7, 8 двумя стерлшями каждый: узел 6* стержнями 2-б и 5-6, узел 7-стержнями б-7 и 4-7 ИТ. д., чем образуются

жесткие диски I и II; оба эти диска соединены между собой стержнем 8-8 и шарниром S, что приводит к неизменяемой системе в целом. Аналогично неизменяемость прикрепления системы к земле требует, чтобы система была присоединена к земле не менее как тремя связями (стержнями), не нересекающимися в одной точке (наличие шарнира в присоединении рассматривается как две связи). По сушеству этого закрепления система и земля ДО.ЧЖНЫ рассматриваться как двадиска.

Указанные условия образования простых систем позволяют проверять неизменяемость системы или указанным путем просмотра ее геометрич. образования из исходной системы (диска) или обратным путем, т. е. приведением заданной системы к исходной; последнее достигается путедх последовате.ть-ного устранения из системы узлов с двумя сходящимися в них стержнями, что в силу из-

Фиг

Фиг. 6.

ложенпото не нарушает неизменяемости остающейся части системы. Например проверка Н. г. системы, показанной на фиг. 5, м. б. сде.дана устранением узла е со стержнями ed и ef, затем узла / со стержнями fd и fg, затем узла d со стержнями dm и de, что приводит к диску сдаЬ, явно неизменяемому, как образованному из двух тр-ков и прикрепленному к земле Е тремя стержнями 1,2,3, не пересекающимися в одной точке. Неизменяемость системы, показанной на фиг. 6, определяется путем устранения шарнира II с двумя дисками 11-1 и II-III, затем, после устранения шарнира VI с двумя дисками VI-VII и VI-V, приводим к системе, образованной из двух дисьсов III-IV и V-IV, соединенных шарниром IV и стержнем аЬ (земля с неподвижными шарнирами а и Ь). Такая простая поверка Н. г. систем возможна только в тех случаях, если сама система построена простым геометрич. образова- / нием без введения заменяющих стержней и других условий (см. Система), что приводит к отсутствию в таких системах узлов либо шарниров с двумя стержнями или дисками (фиг. 7, 8, 9 и др.).

В таких системах поверку неизменяемости следует производить, пользуясь условиями кинематики. По одному из них относительное смещение трех дисков возможно только в том случае, если три относительных мгновенных полюса этих дисков лежат на од-Hoii прямой (см. Кинематический метод). По ЭТОМУ условию система, показанная на

Фиг. 7.

фиг. 7, будет изменяема, т. к. относительные мгновенные полюсы I-II, II-III, I-III ее-стерлшей 1,11 я III лежат на одной прямой. Система, изображенная на фиг. 8, будет изменяема, так как мгновенные полюсы DE,. BE и BD, относяши- fBo

еся к трем дискам: /*

Е-земля, D-стер- !

жень и В-ферма, /;! лелсат на одной пря- / мой DE-BD; но до- / статочно только из- /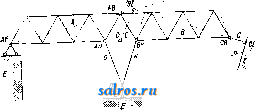

Фиг. 8.

менить направление опорного стержня С, что вызывает смещение полюса BE с прямой DE-BD в точку В'Е', и система станет неизменяемой.

Исследование неизменяемости путем определения мгновенных полюсов нередко приводит к очень сложным построениям, почему целесообразнее пользоваться другим условием кинематики-построением плана скоростей (см. Кинематический метод). При определении этим способом внутренней неизменяемости системы из нее выделяют один из стерлшей или дисков, действие которого на остальную систему заменяется силами X (фиг. 9). С устранением стержня или диска система получает возможность смещения узлов, что позволяет построить для нее план скоростей, обозначенный на фиг. 9 цифрами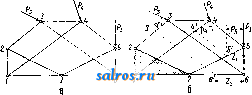

Фиг. 9.

со значками . Для построения плана, диск 1-2-7 (фиг. 96) принят неподвижным и относительно его определены изображающие точки плана (см. Кинематический метод) по исходной скорости 3-3. Если при построении плана скоростей не получитсй^ фигура, подобная фигуре исходной системы (фиг. 9), то система неизменяема. При получении подобной фигуры выражение воз-молшой работы приводится к виду:

что указывает на невозможность установить равновесие, т. е. указывает на изменяемость системы. На фиг. 10 путем построения плана скоростей определена неизменяемость системы относите.чьно ее опорных закреплений. Для этого в системе устранена опорная связь А5, и для оставшейся части системы: