• Что такое фактурная штукатурка
• Выбираем сухие строительные смеси
• Преимущества напряженного железобетона
• Что влияет на выбор кровельного материала
• В чем преимущество пробковых полов

Н. представляет собой разность статич. Н. и потери Н. до данной точки водопровода. Напорная линия изображает динамнч. Н. в данной точке водовода. В силовых трубопроводах, где Н. вообще очень велик, динамич. Н. при установившемся релсиме течения, так лее как и в обычном водопроводе, ниже статического вследствие потерь, к-рые определяют собой кпд водопровода. Нри запирании трубопровода с протекающей в нем жидкостью происходит вследствие гидрав-лич. удара следующее явление: динамич. Н. быстро повышается и молеет достигнуть значительной величины, превышающей статический Н. Это явление вообще опасно для труб и при быстром закрытии затворов может повлечь за собой разрыв труб вблизи аадвижки и порчу водовода. Для устранения этого опасного явления предписывается мед.ченное закрывание затворов в течение нескольких минут (см. Гидравлика). В водопроводном деле при подводе воды к источникам потребления, как наир. к пожарным гидрантам или водоразборным кранам, необходимо иметь некоторый избыток Н. у гидранта или крана для расходования этого Н. при пользовании источником потребления, например для создания пожарной струи. Этот избыток Н. в данной точке сети носит название свободного Н. Свободный Н. для каждой точки водопроводной сети д. б. не менее онределеиной величины.

Лит.: Е с ь м а н И. Г., Гидравлика, 3 изд., Тифлис, 1930; Б р и л и н г с. Р., Пособие для проектир. и расчета водопроводных линий и городских сетей, 2 изд., Москва, 1930; Павловский Н. Н., Гидравлика, Ленинград, 1930; Б an к i О., Eprgie-Um-wandlungen In Flussigkeiten, В. 1, В 1921; см. tslk-же Гидравлика. i,B- Брипинг.

НАПОРНЫЕ БАНИ, искусственные сооружения, вместилища, устраиваемые для хранения жидкостей и располагаемые на высоте, достаточной для питания раздаточной сети труб под естественным напором этих жидкостей. В водопроводном деле Н. б. служат, с одной стороны, для регулирования неравномерности между притоком воды и расходом ее в водопроводной системе и, с другой,-для создания напора в сети во время питания последней от бака. Первое достигается достаточной емкостью бака, второе- расположением бака на достаточной высоте. В общем Н. б. ничем не отличаются от водонапорных резервуаров (см.). с. Брилинг.

НАПРАВЛЕННОЕ РАДИО осуществляется нри помощи направленных антенн (см. Волновал антенна, Гониометр, Замкнутая антенна. Лучевая антенна); используется для направленной передачи и направленного приема радиосигналов. По терминологии, принятой 9 Всесоюзным электротехническим съездом (ВЭС), направленная антенна - антенна, обладающая свойством излучения или приема радиоволн вдоль некоторых направлений в большей стенени по сравнению с другими. Практически направленность антенн рассматривается иреиму-щественно в горизонтальной плоскости (т, е. изучается неодинаковое по различным ази-MjTaM от места раснололсения антенны излучение или прием). Однако теоретически, а в последнее время и практически (для коротких волн), Н. р. представляет не мень-

Т. Э. т. XIV.

шее значение и в вертикальной плоскости. Направленность антенн обычно характеризуется диаграммами направлепиости (или, иначе-полярными диаграммами): для горизонтальной направленности-это кривая, которая соединяет концы радиусов-векторов в различных азимутах, представляющих значения напряженности (см.) электрич. или магнитного поля излучаемой или принимаемой электромагнитной волны (или величины, им пропорциональные). Практически направленный радиоприем реализуется на всем диапазоне частот; направленное излучение применяется преимущественно только на коротких, промежуточных и реже - средних волнах (разделение диапазона частот на категории-см. Несущая волна).

Направленный радиоприем. В зависимости от частоты воспринимаемых колебаний цели применения направленных антенн таковы: 1) на длинных волнах направленные антенны в радиосвязи применяются гл. обр. для борьбы с атмосферными разрядами (см.) и с явлениями эхо у антиподов, а также с мешающим действием других передатчиков; 2) на средних волнах-гл. обр. для уменьшения помех от блилеайших станций и отчасти для уменьшения действия на прием атмосферных разрядов; 3) на промежуточных, коротких и ультракоротких волнах - в целях уменьшения замирания (см.) сигналов и для устранения эхо . Кроме того сложные системы направленных радиоприемных антенн имеют назначение воспринимать большее количество э.лектромаг-нптиой энергии волны корреспондента. Наконец на всем дианазоие частот только при помощи Н. р. при приеме возможно осуществить пеленгацию (см. Пеленгатор), т. е. определить направление поступающих электромагнитных волн. Направленный прием, как более часто применяющийся на практике, в отношении диаграммы направленности может быть классифицирован согласно помещаемой ниже таблице.

Направленное излучение. Основной целью направленного излучения в радиосвязи является концентрация энергии электромагнитной волны в онределенном, наперед заданном направлении (или направлениях), с целью: увеличения сил и ноля на месте приема (у корреспондента) и уменьшения помех другим приемникам. Наиравлен-ное излучение практически применяется в следующих формах: 1) для радиосвязи- только на коротких волнах (см.); 2) для радионавигации: а) в форме радиомаяков (см.), б) в виде самоориентирующих радиостанций (вращающиеся рамки, контурный самоориентир-см. Радиомаяк и Пеленгатор). Оба последних применения используют область средних (реже ультракоротких) волн. Сравнение этих форм использования, еще неустановившегося пока характера,-см. Радиомаяк. Диаграммы направленности при направленном излучении: 1) при коротких волнах- комбинационные характеристики (см. Лучевая антенна), 2) при средних-две окружности или же кардиоида (другие формы встречаются реже).

Лит.: Куксенко П. Н., Направленный радиоприем, М., 1930; Б а ж е н о в в. И., Направляемый

Классификация диаграмм направленности для различиых антенн.

радиоприем, Радиотехник , Н.-Новгород, 1919-21, 8-15; Keen R., Wireless Direction Finding and Directional Reception, L., 1927; W a 11 6 г L., Directive Wireless Telegraphy, L., 1921; M e s n у R., Usage des cadres et radiogoniometrie. P., 1925.-0 направленном радиоизлучении: Ргос. of the Inst, of Radio Engin. , N. Y., 1928.-О направленном радиоприеме: Jahrb.d. drahtl. Telegr. u. Teleph. , В., ab 1928.

НАПРЯЖЕНИЕ электрическое или магнитное, работа электрич. или магнитных сил при переносе единицы положительного заряда (электрич. или магнитного) вдоль данного пути. Таким образом Н. есть линейный интеграл вектора uanpsuncenuocmu (см.) поля:

и = J н dr.

Н. зависит не только от положения начальной и конечной точки, но и от самого пути. Так например, показания вольтметра, вообще говоря, зависят от расположения соединительных проводов. Необходимым и достаточным условием, чтобы это Н. не зависело от формы пути, является отсутствие завихрений у вектора наиряженности: rot лг=0.

Другими словами, линейный интеграл вектора напряженности поля по любой замкнутой линии, Н. обхода в поле, при этом условии должен равняться нулю:

MdrO.

В этом случае Н. вдоль данной линии зависит только от положения начальной и конечной точек данной линии и м. б. выражено как разность значений скалярной функции, называемой потенциалом (см.) этих точек. Т. о. Н. может быть выражено в виде разности потенциалов только в безвихревом ноле.

Электрическое Н.-линейный интеграл вектора напряженности электрического поля. Международной единицей электри^-ческого Н. является один вольт. В настоящее время для промышленных испытаний построены лаборатории, где регулярно получается Н. до 2 ООО ООО V; с другой стороны, например в тонких физических исследованиях приходится встречать Н., измеряемые в микровольтах. В технике весьма неудобно иметь дело с Н., зависящим от пути, соединяющего данные точки. Поэтому в большинстве случаев электрическое Н. стараются изображать в виде разности потенциалов. Так например, при изучении явлений переменного тока, когда вектор напряженности поля обладает завихрениями, сплошь и рядом приходится иметь дело с электрич. П., зависящим от пути. В этом случае обычно в цепи электрич. тока рассматривают отдельно П. на зажимах и вводят понятие индуктированной эдс для того, чтобы изображать вихревое электрич. поле в виде потенциального (см. Индукции закон).

За последнее время, особенно в герм, литературе, перестают говорить об индуктированной эдс и вместо этого применяют термин индуктированное электрическое Н. Электрич. Н. измеряется при помощи вольтметров или электрометров, а на линиях высокого Н. также ири помощи клайдоиографов (см. Осциллограф).

Магнитное Н., или магнитодвижу-пщя сила,-линейный интеграл вектора наи-1)яженности магнитного ноля. Международной единицей магнитного напряжения является один ампер или ампер-виток. Магнитное Н. молсет быть выралкено в виде разности магнитных потенциалов в той части ноля, где отсутствуют завихрения вектора напряженности магнитного поля, т. е. там,где отсутствуют электрич. токи. Магнитное Н. измеряется баллистич. методом при помощи пояса Роговского. Постоянное магнитное П. не оказывает заметного действия на человеческий организм. я, Шпильрейн.

НАПРЯЖЕНИЕ в механике, см. Напряженное состояние.

НАПРЯЖЕННОЕ СОСТОЯНИЕ, такое состояние тела, ири к-ром деформация его под действием уравновещениых внещних сИл прекратилась и все частицы тела пришли в равновесие. Если в теле, находящемся в таком состоянии, провести мысленно разрез, то обе части его доллшы находиться в равновесии, что возможно только нри условии, что по поверхности разреза будут действовать какие-то внутренние си.пы, равнодействующая к-рых будет уравновеигивать действие внешних сил, прилол1:ениых к калодой части тела. Эти внутренние силы называют внутренними силами упругости и соответственно II. с. тела часто-с о с т о я-нием упругого равновесия. В общем случае внутренние силы распределяются по поверхности сечения конечных размеров неравномерно, но если мы выделим вокруг точки А на поверхности сечения v очень малую площадку Дсо, то в пределах такой плонщдки можно допустить, что силы распределены равномерно. Деля на площадь этой площадки передаваемую через нее часть общей равнодействующей внутренних сил R, получим среднее значение напряжения для площадки Дсо. Уменьшая эту площадку до нуля и притом так, чтобы контуры площадки заключали в себе точку А, мы для

в пределе получим и а и р я лс е н и е в

точке А:

cr=lim() = , (1)

К-рое т. о. для данного сечения v при неравномерном распределении напрялшпий определяет интенсивность внутренних сил упругости в точке А.

Величина равнодействующей R определяется из условия равновесия ее с внешии-АП1 силами, ирилол-сенными к рассматриваемой части тела. За направление напряже-]шя <т принимается наиравление равнодействующей, относящейся к данной точке; т. к. паправление это вообще неизвестно, то при изучении Н. с. изучают слагающие папря-жеиия: п-нормальное к поверхности площадки и t-касательное к ней. Нормальные

напряжения вызывают растяжение или сжатие материала в точке, а касательные-сдвиг или срезывание. В общем случае напряжение в точке характеризуется слагающими по трем осям координат, для чего вводятся следующие условные обозначения. Ыапрял-:е-ние, относящееся к площадке, перпендикулярной к оси х-ов и параллельное самой оси, обозначается двумя одинаковыми индексами %a;a;; очевидно, ЧТО ЭТО напряжение, нормальное к площадке. Напряжения, относящиеся к той же площадке, по параллельные другим осям, обозначаются также двумя значками, причем первый определяет площадку, к к-рой относится напряжение, а второй - направление напряжения: 1., t и т. и. Эти напряжения очевидно являются касательными к площадке, нормальной к оси х-ов (фиг. 1). При опреде.тении направления этих напряжений принимают нормальные напрялеения растягивающими, т. е. вы-

OC--dx 0B=d2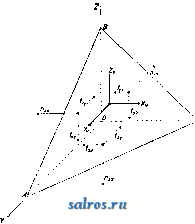

-С X

Фиг, 1.

ходящими из сечения; направления же касательных напряжений принимают по соображению с направлением нормального на-нрялеения; если последнее направлено в сторону положительного направления оси, то направление касательных напряжений принимается ио положительному направлению двух других осей; если же направление нормального напряжения принято по отрицательному направлению оси, то и наиравление касательных наирялеений принимается по отрицательным направлениям соответствую-Щ1Ех осей (фиг. 1).

Через любую точку тела можно провести бесчислеппое множество различно направленных площадок, но напряжение по любой из этих площадок м. б. найдено, если известны напряжения по трем взаимно перпендикулярным площадкам, проходящим через ту же точку, что вытекает из условия равновесия тетраэдра О АБС, к-рый можно представить себе вырезанным из тела в рассматриваемой точке О плоскостью v (ABC) и тремя плоскостями по направлению координатных осей, на к-рых плоскость v отсекает бесконечно малые грани dx, dy и dz, стремящиеся к ну.тю, что позво.тяет считать напряжения во всех четырех плоскостях тетраэдра отнесенными к точке О тела. Если обозначить п.тощадь грани АБС через со, то пло-

щади остальных граней тетраэдра определятся величинами

ft> cos {х, v), Q> cos {у, v), щ cos (z, v). Из условия проекции на каждую из осей после экращения на получаем: X,= ncos(a;,u)+fj,cos (y,vW cosC,)) Y=nyyCOs(y,v)-\-txycos {x,v)+ty co3(z,v) \.(2) Z cos {z,v)+ty cos (y,v)+tcos(x,v)) Таким образом слагающие напряжения по

плоскости V определяются девятью слагающими напряжений по координатным плоскостям тетраэдра. Из рассмотрения прямоу-гольн. параллелепипеда (фиг. 2), который вырезан из -x тела у той же точки, следует, что существует такая взаимность по равенству касательных напряжений между собой:

Действительно, из условия моментов всех сил, приложенных к парал.пелепипеду, относительно осей, проходящих через ц. т. его, для оси параллельной оси ж-ов имеем:

t dxdz- + [t + lyjdy)dxdz-{--t,y dydx . - [t,y + dz) dxdy. f = 0.

Пренебрегая бесконечно малыми высшего (4-го) порядка, получим:

tys dxdzdy - dxdzdy = О,

Фиг. 2.

ijs - гу

Аналогично может быть доказано, что

Эта взаимность между касательными напряжениями приводит к тому, что для определения слагающ1сх напрялсений в любой плоскости надо знать шесть элементов составляющих напряжений в трех координатных плоскостях.

Проекция напряжения в плоскости v на нормаль к этой плоскости определится как сумма проекций составляющих

= cos (V, ж) -Ь F cos (v,y)-i-

+ Zcosiv,z), (4)

или, подставив значение XYn Z и сделав приведение, получим:

-f njcos (v,z) + 2tyCos{,v, x)cos(v, y) 4-+2tjcos{v,y)cos{v, z) 4-+ 2tj.gCOS(v,x)cos(v, z). (5)

Если площадка v поворачивается вокруг точки О и если в соответствии с ее поворотом откладывать по нормали к площадке отрезки е= liVny, то координаты концов этого отрезка будут:

x = Q cos(гз, ж); у = qco${v, у);

г = 9 cos(v, 0). (6)

Подставив значения хгосинусов в выражение (5) напряжения п^; получим:

nx-\-nyyy+n z+ .

+ 2ty ху+ 2ty,yz + жг = 1, (7)

т. е. уравнение второго порядка. Изменяя направление координатных осей, можно выбрать такое направление их, что коэф-ты при членах с произведенисхм координат будут равны 0. Для таких осей слагающие касательные напряжения будут равны нулю, и останутся только нормальные напряжения. Плоскости, к к-рым относятся эти оси, носят названия главных плоскостей сечения, а относящиеся к ним нормальные напряжения-г данными нормальными напряжениями Wjg и W33. Величины этих нормальных напряжений определяются корнями кубического ур-ия:

- и -Ь (%-, -h пуу -Ь И^г) п^-(пхх пуу + пуу

+ пзи^ха - Чг -цу- tlx) + (п^х уу +

+ .tj-y txz уг ~ хх цг ~ уу овг ~ **аг Чх)-0. (8)

Оно получается из ур-ия (2) подстановкой в него вместо ве.чичин Х^, Г^, значений их. к-рые выражены через главные нанрялсе-ния п:

Хр = тесо8 (ь,х); r =ncos (v,y); = ncos (v,z) и исключением из полученньгх этим путем трех ур-ий косинусов углов, связанных между собой условием

cos* (г , ж) -Ьcos (v, у) + cos (v,z)= 1. (9) Из выражений (6) и (7) непосредственно видно, что сумма нормальных напряжений независимо от направления координатных осей есть величина постоянная:

1хх + пуу + =Щ+Щ+па=- Const.

Если отложить отрезок по направлению нормали к плоскости v от начала координат главных плоскостей, то координаты вершины отрезка будут:

ж = = щcos(v, ж); у^п^у= щ cos(v, у);

z = 71 = щ cos (v,zy,

но так как косинусы углов связаны условием (9), то

след. при вращении площадки полное нор-лгальное напряжение к ней при различных положениях ее определяется отрезками, вершины к-рых очерчивают поверхность эллипсоида, называемого эллипсоидом напряжений. Когда одно из главных напряжений обращается в нуль, то эллипсоид обращается в эллипс, и наирял^ения для всех полол^ений площадки будут лежать в одной плоскости; такое состояние тела называется НЛО с к и м н а п р я ж е н и ы м с о-стоянием (плоская задача). Если два главных напряжения обращаются в нуль, то получится линейное напряженное состояние. Большинство технич. задач приводится к плоскостному и линейному Н. с, которые представляются более простыми для решения, чем пространственные, и рассматриваются в курсах сопротивления материалов. Вопросы о пространственном напряженном состоянии рассматр -ваются в курсах теории упругости.

При плоскостном Н. с. тетраэдр, показанный на фиг. 1, приводится к треугольн. призме (фиг. 3) с бесконечно малыми сторонами dx и dy и длиной по оси Z, равной единице. В этом случае напряжения

nz = izx=izy=- Если же обозиалить угол наклона площадки V к оси ж-ов через а, то напряжение щ, нормальное к

этой площадке, определится следующим вы-ра>кением:

=ПухВ1па -f Щу cos а = = Пд. sin а + Пу c0s2 а -\- ty sin 2а, (10)

и напряжение касательное к ней, определится выражением:

h = cos а - Щу sin а =

= I (Па; ~Пу) sin 2а-i-ty COS 2а. (11)

Наибольшие значения нормального и касательного напряжений определяются из условий:

da da

По первому из этих условий будем иметь: 2%cosaiSinai-2wsinaiCosai -f 2a;yCos2ai= О, откуда следует, что площадка с наибольшим нормальным напряжением наклонена к оси х-ов под углом

(12)

Выразив величины cos а и sin а^в функции угла 2ai, из (10) получим:

= (Wa; + Пу) - 2 (п^-Пу) COS 2aj -f- /arj, sin 2ai. (13)

Подставив в него значение cos 2аi и sin 2ai из (12), получим выралеения главных напряжений, максимального-и минимального-щ в таком виде:

x=(w, + n)-f (Пх-Пу) + 41у)

П2=1{п^-\-Пу)-1у^(п^-пуу + иЬу-, (14)

оба напряжения те и взаимно перпендикулярны. Из сложения их вытекает, что

Щ + Щ==Па. + Пу = Const. Из вьц)ажепия (11) касательного напряжения tg видно, что для главных плоскостей течения {= О. Наибольшее значение касательного напряжения определяется из условия = О, т. е.

(Па; - cos 2а2 - 2f sin = О, которое удовлетворяется при условии

tg2a,= < -V

ИЗ чего следует, что п.лощади сечения с наибольшим и наименьшим значениями каса-7ельногб напряжения направлены под углом 02 = 1 + 45° и 02 = 0 + 135° к координатным плоскостям или под углом 45° и 135° к главным плоскостям сечения. Величина наиболь-щего ti и наименьшего tz касательного напря-

жения определится после подстановки значения tg 2а2 в выражение (11):

= \УЬг,-ПуУ-{-Щу; h = (16)

Величины напряжений по различным плоскостям сечений, проходящих через точку, м. б. определены графически при помощи круга Мора, На фиг. 4 построен круг Мора на главных напряжениях и (в данном частном случае значения щ и щ взяты разных знаков, а именно: -положительное, а щ - отрицательное). Разность этих напряжений [пх - п.] образует диаметр круга. Если взять какую-либо точку С круга и опустить из нее перпендикуляр на диаметр, то из чертежа нетрудно видеть, что

OjD= 2 (Щ + (Wi-na)cos 2а = Пу,

CD= 2 С*!-*а) sin 2a=ty,

т. е. отрезок 0D по диаметру круга, как абсцисса точки С, определяет величину нормального напряжения Пу в плоскости С1, наклоненной под углом а к главной оси (13),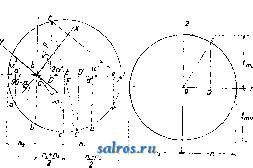

Фиг. 4.

Фиг. 5.

и отрезок cd определяет величину касательного напряжения tyx в той же плоскости (11). Напряжения и ty в плоскости перпендикулярной определяются отрезками 0D и dc. Из чертежа видно, что истинное положение и величина напряжений в этих площадках определяются отрезками

р = и р' = Уп[+1Еу.

На фиг. 5 показан круг Мора для случая чистого сдвига, когда

На фиг. 6 сделано построение эллипса на-прял^ений на полуосях 01 = ni и 02=П2 и кривых (роза), характеризующих развитие нормальных и касательных напряжений по направлению любых плоскостей. Для построения этих кривых проводим на круге Мора ряд плоскостей сечении 1-а, 1- 1-е и такие же плоскости проводим через центр эллипса. Откладывая по направлению перпендикуляра к каждой из этих плоскостей отрезки Оа, Ob, Ое, получаем по ним кривые 2 а' Ь' Осd ei, характеризующие изменение величин наибольших нормальных наирял^ений. Откладывая в самих плоскостях отрезки Оа , Ob ,Ое , получим кривую Оа Ь с d е О (на фигуре 6-.пунктирная), определяющую величины касательных напряжений в разлнчт

ных плоскостях. Указанным построением такие кривые могут сыть получены для ка-к-дой четверти. Проведя например плоскость под углом а к главной оси 1-1, получим в пересечении ее с пунктирной кривой точку Ci, определяющую величину касательного напряжения OCi=tya;, проведя к той же плоскости перпендикуляр, получим в пересечении его со сплощной кривой точку D, определяющую величину нормального напряжения ОП =Пу. Отрезком ОС = р, вершина которого лежит на эллипсе напряжений,

Фиг. 6.

определяются величина и направление напряжения р в рассматриваемой плоскости сечения (точки эллипса напряжений, соответствующие плоскостям а, Ь,...е ошечепы буквами tti, bi, Cj). В общем же случае Н. с. какой-либо точки тела, определяемого напряжения.ми rii > > по трем главным плоскостям, зависимость между напряжениями в любых плоскостях определяется тремя кругами (фиг .7): для плоскости сечения, параллельной плоскости 1 -2, -кругом J.B, для плоскости сечения, параллельной плоскости i-3,-кругом J.С и для пло-

- - п.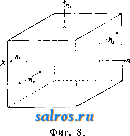

Фиг. 7.

скости, параллельной 2 - 3, - кругом ВС. Для плоскостей, пересекающих все три координатных оси, напряжения в них изображаются координатами точек, лежащих в заштрихованной площади.

Выведенные выше величины наибольших суммарных напрял^ений вырал^ены в функции слагающих напрял^ений, определяемых по равнодействующими моментам,вызываемым в сечении действием внешних сил. Но по закону Гука всякое напряжение является линейной ф-ией от деформации (см.). В телах изотропных, имеющих одинаковые упругие свойства во всех направлениях, эта ли-

(18)

(20)

нейная зависимость упрощается (см. Деформация, ф-лы 9 и 10), что позволяет величины наибольших напрялсений по направлению главных осей, обозначенные условно через [и], выразить следующими ф-лами (фиг. 8): [щ] =Eei = ni~r] (щ + щ) 1щ] = Ее2 = щ-п (щ + Пз) [W3] =Ее = щ-г] (щ -f щ)

Эти напряжения в главных плоскостях, выраженные через суммарную деформацию, носят название приведенных г л а в-ных напряжений; в них г]-коэфициент Пуассона. При илоскостнод! действии сил 3=0, потому приведенные напряжения определяются выражениями:

[п1] = Щ~г]п2 и [п2] = п2-г}П^, (19)

к-рые после подстановки в них величин и 2 по ф-лам (14) приводятся к виду: Ы = i (1 -г1)(п^+Пу) +

+ + V)Vin-nyf+4ily, [Щ] = I- (1 - J7) (n-f Пу) -

~ ИИ- П)У(Пх-ПуУ+4Щ.

Величины касательных напряжений определяются по углам сдвига е^у, еу, е^ (см. Деформация, ф-ла 9):

ху~ Ge-y, ty- GCyg. txz~Gexz, (21) где G-модуль упругости при сдвиге.

Входящие в выражения наибольших нормальных и касательных напрял^ений величины напряжений Пхх, Пуу, п^, ty, ts, ty в координатных плоскостях определяются из условий равновесия тела при рассечении его по направлениям этих плоскостей. Для их определения сложное действие внешних сил на тело расчленяют на простые: действие продольной силы (растяжение и сжатие) , действие поперечной силы (сдвиг и срезывание), поперечный изгиб и кручение (см. Изгиб, Кручение). При действии продольной силы N, направленной вдоль оси бруса и приложенной в центре тяжести сечения его, напряжения в сечении, нормальном

к оси бруса, будут tyo, Пх=±=щ,

из чего следует, что нормальное напряжение в этом сечении является главным и 2=0. В плоскостях, нак.т10ненных под любым углом а к оси, напряжения будут определяться выражениями (формулы 10 и 11):

W =WiCOs2a = cos2a; f =J-sin2a.

Наибольшее касательное напряжение имеет место в сечениях, наклоненных под углом

а = 45° к оси бруса, когда t = ni. При действии поперечной силы Q, нанравленной перпендикулярно к оси бруса, деформация бруса всегда сопровождается не только сдвигом сечения одно относительно другого, но и изгибом. В отдельных случаях практики (срезывание в заклепках, во врубках и т. п.) принимают, что касательное напряжение в сечении, нормальном оси, распределяется равномерно по сечению и определяется величиной txy= ~, причем в этом сечении

а;= **з/= о, что соответствуст случаю чистого сдвига (ф-ла 17). Наибольшие и наименьшие нормальные напряжения имеют место в пло^

8700

скостях, наклонных под углами ±45° коси; величина их (ф-ла 14): Пу=-щ^ ш

При кручении, возникающем под влиянием момента М^, плоскость к-рого нормальна к оси бруса, в сечениях бруса, нормальных к оси, развиваются только касательные напряжения, к-рые для брусьев круглого сечения определяются величинами (см. Кручение):

ЧТО соответствует случаю чистого сдвига (ф-ла 17) (7о - полярный момент инерции площади поперешого сечения). Наибольнше нормальные напряжения имеют величину (ф-ла 14);

и относятся к сечению, наклоненному под углом 45° к оси бруса (ф-.ча 15).

Напряжение при чистом изгибе, вызываемое действием сил, лежащих в одной из пло- скостей, совпадающих с направлением глав- ных осей поперечного сечения бруса (фиг. 9), опреде.тяется выражением (см. Изгиб):

М~ My rs

;= j~y или = -j Z И Пу=0,

в к-рых Jj, и ly-моменты инерции сечения, а, у я Z-координаты рассматриваемой точки. Очевидно, что наибольшие напряжения имеют место в крайних точках сечения

Mg м,

или

в к-рых и Wy-моменты сопротивления сечения. В большинстве случаев практики изгиб сопровождается действием поперечной силы, и тогда напряжения в отдельных точках сечения определяются величинами:

в к-рых Sji y-статич. момент частрт сечения от уровня рассматриваемой точки О до контура сечения (фиг. 9), Ъу-ширина сечения на уровне точки. Одновременное действие изгибающего момента и поперечной силы является одним из наиболее распространенных случаев комбинированного действия -сил. Величина наибольших нормальных и касательных напряжений, определяемых по формулам (14) и (16), будет меняться в зависимости от положения точки в сечении. Для точек, наибо.чее удаленных от оси сечения, напрялсеиия будут:

щ = М. п, = 0; 1 = 0;

для этих точек сечение, нормальное к оси бруса, является главным сечением; и т. к. для него 2=0, то эллипс напряжепий в этих точках обращается в прямую линию (фиг. 10, 1-1 в крайней верхней точке сечения и 2-2 в нижней). Для точек, расположенных на оси бруса,

Щ = Щ = О, tf = - ,г„ = 9;

для этих точек в сечении, нормальном к оси, имеет место чистый сдвиг; эллипс папряже-ЩИ.Я в этих точках превращается в круг.

Для всех остальных точек сечения главные напряжения определяются величинами (14):

и наибольшие касательные величиной (16):

причем нормальное напряжение будет направлено под углом (13):

l.by.M~y~ МЪуу

На фиг. 10 показано нриближенное очертание и нанрав.ление осей эллипса напряжений в этих точках.

При сложном действии внешних сил и моментов, вызывающих каждое в отдельности нормальные напряжения, величина сум-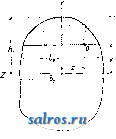

Фиг. 9.

марного нормального напряжения определяется на основании закона о независимости действия сил простым алгебраич. сложением по величине и знаку. Так напр., при внецентренном действии продольной силы, приложенной к точке с координатами а в. Ь, что сопровождается действием в сечении бруса продольной силы JV и моментов Мх = = Na и My=Nb, нормальное напряжение для любой точки сечения с координатами х и у определяется выражением:

п

где и Qy-соответственные радиусы инерции, из чего следует, что в общем случае действия силы и МО- , 2 ментов нормальное наирял^ение распространяется по сечению по з а к о-ну плоскости. При одновременном действии на брус круглого сечения изгибающего и закручивающего моментов, что сопровождается развитием в сечениях бруса нормальных к оси напряжений

Фиг. 10.

х-~гУ,

QSh-if

. м

величины наибольшего и наименьшего нормальных напряжепий будут иметь место в точках, наиболее удаленных от нейтрального слоя (фиг. 11), и определяются из следующих выражений (14):

Наибольшее касательное напряжение в той же точке будет (16)

Наибольшее же касательное напряжение в крайних точках нейтрального слоя определяется из суммирования касательных на-

Фиг. 11.

пряжений (фиг. 11), имеюших в этих точках одинаковое направление как при изгибе, так и при скручивании (16):

2rh Iz

В качестве условия прочности при рассмотрении комбинированного действия кручения и изгиба чаще пользуются ф-лой приведенных главных напряжений (20), по к-рой наибольшее нормальное приведенное напряжение определяется величиной:

при rj = 0,3 это выражение принимает вид: Ы = - (0,35Мз + 0,65 УЖ+Щр),

выражение, известное под названием ф-лы Сен-Венана.

Вопрос изучения Н. с. тела имеет своей целью определение необходимых размеров тела по условиям прочного сопротивления материала самого тела. Условием прочного сопротивления всякого тела, входящего в состав машины или сооружения, является сохранение им первоначальной своей формы, т. е. отсутствие в теле остаточных линейных и угловых деформаций; отсюда следует, что напряжения в частях тела д. б. таковы, чтобы наличие их в теле не сопровождалось появлением остаточных деформаций. В связи с этим выбор размеров каждого тела Ш1И каждой детали маии1ны ограничивается величиной допускаемого па-пряжения. Величина допускаемого нормального напряжения щ выбирается как некоторая доля от временного сопротивления R материала или его предела упругости,

т. е. По = R, где /с-коэфициент запаса

прочности, величина которого изменяется сообразно Q однородностью упругих свойств материала и работой машины или

соорулсения. Самый расчет прочности делается по одной из формул напряжений в. соответствии с тремя теориями прочности (см. Прочность). Если расчет делается по первой теории прочности, т. е. по величине наибольшего напряжения, что справедливо для случая линейного действия сил на тело, то используется форму.ла (14) главных напряжений, и напряжение i д. б. щ. Когда расчет прочности де.лается из условия, что линейная деформация пе должна превосходить известного преде.ла, то в случае пространственного действия сил используется формула (18), по которой

[Щ] = Щ -Г]{Щ + Пз) Мо.

При плоскостном действии сил определение напряжения делается по ф-лам (19) или (20), по к-рым

[Wj] = 1 - щ.

Если расчет производится по третьей теории прочности из условия, что в теле не д. б. остаточных угловых деформаций, то допускаемое напряжение на сдвиг 4 определяется из выражения касательного напряжения через главные (ф-ла 11 при а = 45°)

Расчетное напряжение определяется но ф-.ле (16) из условия tg. 0,5 щ.

Изучение Н. с. при сложном действии сил не всегда разрешимо при существующем развитии теории упругости и сопротивления материалов. Существенную помощь в этом изучении при плоскостном действии сил оказывает оптический метод (см. Деформация), основанный на том, что запаздыванием лучей, пропускаемых через напряженную пластинку, определяется разность главных напряжений, т. е. величина наибольших касательных напряжений 21=Пх - п^. При пропуске через пластинку белого света последний в силу явления хроматич. поляризации разлагается на ряд цветов (кольца Ньютона), которые оттеняют распределение напряжений по пластинке; так, одноцветность показывает, что разность {п^-п^ одна и та же; это дает возможность проследить развитие в теле т. н. траекторий напряжений (см. Деформация, вкл. лист). Места, остающиеся на пластинке обесцвеченными, показывают, что в них отсутствуют сдвиги, т. е. < = О, а это соответствует равенству главных напряжений. При на.личиИ' эталона, подвергающегося одновременно растяжению определенными силами и в соответствии с этим изменяющего свою окраску, представ.ляется возможным определить разность напряжений ( 1 - г^) по хроматич масштабу (см. Деформация). Наконец, измеряя при помощи точнейших приборов (в сотых долях /л) изменение Ад толщины пластинки в изучаемой точке, можно определить сумму главных напряжений из условия:

Е А(5

где Е-модуль упругости материала пластинки, а г]-коэфициент Пуассона для нее. Таким образом при помощи оптического метода выявляются: направление главных напряжений и величины (Wi-Wa) и (п^+п^),. чем они вполне определяются.

49999999999999

9999

Лит.: Митинский Н., Строительная механика, СПБ. 1914; Тимошенко С, Теория упругости, ч. 1, СПБ, 19 14; Зайцев А., Оптич. метод изучения нанряжениГЬ Л., 1927; Love А., А Treatise он the Mathematical Theory of Elasticity, Cambridge, 1928; F 0 p p 1 A., Vorlosungen uber technisclie Mechanik, 4 Aufl., B. 5, В.-Lpz., 1922; CokcrE., FOppl A. u. Fop pi L., Drang u. Zwang, B. 1. 2 Aufl., Mch.B., 1924, B. 2, Mch.-В., 1920; C о к e r E., The nttermination by Photo-Elastic Methods of the Distribution of Stress, Trans. of the Inst, of Naval Archit.N Ij., 1911. И. Прокофьев.

НАПРЯЖЕННОСТЬ (сила) ноля, вектор , характеризующий электрич. или магнитное состояние данной части пространства. Н. электрическая определяется также как сила, действующая на единицу положительного электрич. заряда. В международных единицах Н. измеряется в V/cjh. Максимальное возможное значение Н. электрического ноля определяется диэлектрич. крепостью среды. Воздух при нормальных условиях вьщерживает около 28 кУ/см. При дальнейщем повышении Н. наступает пробой. В вакууме при крайнем разрежении может существовать Н. в несколько миллионов Y/cM. При наличии электрич. поля в про-водшшах в них появляется электрич. ток, причем плотность этого тока пропорциональна Н.поля. Этим объясняется опасность сильных электрич. полей для человека, т. к. возникающий электрич. ток в теле человека уже при силе в 0,1 А может оказаться смертель-яьш. Существует ряд различных способов для измерения П. электрического поля, но по большей части Н. поля определяется на основании измерения потенциала в поле. До сих пор терминология в отношении Н. электрич. поля еще не установилась окончательно. Нередко Н. поля называют и а-пряжением поля, или градиентом. Однако это наименование неправильно,так как под напряжением понимают линейный интеграл вектора напряженности электрич. поля, а градиентом можно называть только безвихревой вектор, тогда как вектор Н. электрич. поля часто не имеет потенциала.

На. пряженность магнитного поля, или сила магнитного ноля, - это вектор, характеризующий магнитное состояние среды. Формально он м. б. определен как сила, действующая на единицу положительного магнитного заряда . Вектор Н. магнитного поля связан с электрич. током. Напряжение обхода (линейный интеграл вектора наиряженности магнитного поля) вдоль замкнутого контура равно полной силе тока, протекающей через поверхность, окаймленную этим контуром

где Н. ноля измеряется в А/сж,а сила тока- в амперах. На пленарном заседании Международного электротехнического комитета (IEC) в Осло 9 июля 1930 г. было предложено для абсолютной электромагнитной единицы CGS напряженности магнитного поля название эрстед (Oersted). я. Шлильрейн.

Н. поля в радиотехнике. Н. электрического поля электромагнитной волны в радиотехнике-основная величина, характеризующая как закон расирострацения электромагнитной энергии (см. Волны электромагнитные), так и практич. расчеты радиосвязи

между определенньБми пунктами, дальность действия радиовещательных например станций и т. д. Т. к. в радиотехнике пользуются всегда очень слабыми П., то последние измеряются в i>.Y/m, значительно реже в mV/ж. Соотношения между различными системами мер:

а) для Н. электрич. поля Е:

1CGSM= 3-10 10 CGSE = 10-8V/cjw=lp-V/At;

б) для Н. магнитно с поля Н:

1 CGSM = З-ЮЮ CGSE = 1 гаусс = 0,79577 AW[гм; как всегда: Е = с-Н, где с-скорость света, если Е и Н выражены в системе CGSM; вообще Н. электрич. поля выражается в системе CGSE тем же числом, каким Н . магнитного поля-в системе CGSM. В практике пользуются почти исключительно II. электрич. поля.

Н. электрич. ПОЛЯ волны для случая длинных и средних волн (см. Несущая волна), когда допустимо предполол^ение, что электрическое поле волны перпендикулярно к поверхности земли в месте приема, где имеется определепная приемная антенна с вертикальным снинением и действующей высотой h, (см. Антенна), с достаточной для практики точностью характеризует напря-лсение Е' в антенне (см. Излучение и прием): E=Eho . Во всех прочих случаях, в частности при промежуточных и коротких волнах, где имеется достаточно выраженная горизонтальная поляризация электрического поля волны (см. Волны короткие), необходимо оперировать с вертикальной и горизонтальной составляющими Н. того н^е поля или- что нагляднее-с величиной вертикальной составляющей (так же как и в предыдущем случае) и затем отношением между вертикальной и горизонтальной составляющими Н. того же .электрич. поля.

Теоретически наибольшая мощность, полученная и поля приемной антенной, зависит только от И. и длины волны Л: а) для приема без обратной связи (см. Ламповый приемник): Ртах--. б) то же при приемнике с

ч. Е2А2

обратной связью: Ртах=т7 практически вследст-

160л'

вне неосуществляемости равенства активного сопротивления антенны и сопротивления излучения (Bi<JR> P<Pmax достигая единиц-десятков % от Ртах-Нахождение величины Н. электрич. поля радиоволны паданном расстоянии от излучающей системы является конечной практич. целью законов распространения электромагнитных волн, и эта задача пока еще не решена полностью; для Н. поля (амплитуды) вблизи передатчика (область относительно сильного для радиотехников поля) действительна идеальная формула радиопередачи, по которой

E = 3V20- -р, а

где Ps-мощность, излученная по полусфере радиусом d. Для области слабого поля некоторое приближение к практике дают полуэкспериментальные формулы (см. Волны э.яе-ктромагнитные). В виду недостаточной удовлетворительности существующих способов определения излучающей способности радиостанций (первичная моиность, мощность в антенне, момент тока антенны, мощность, подводимая к анодам последнего лампового каскада - вольтамперный способ). Ин-том радиоишкенеров в Пью Порке (IRE) предложено осенью 1929 г. характеризовать в частности радиовещательные станции вели-чгной Н. электрич. поля волны последних, измеренной в 8 равноудаленных (по кругу) точках, радиусом в 5 миль (8 kjm) от пере-,

датчика; среднее из восьми измерений напряжений на расстоянии 5 миль (8 км) от передатчика и должно характеризовать (радиовещательную) станцию.

Норм Н., между народно установленных, пока еще не существует. Однако для радиосвязи имеются рекомендации предварительной Вашингтонской конференции (1921 г.), по которым требуются следующие Н. электрического поля:

1) Радиотелеграфный слуховой прием: А) Н -затух:\гош;ие колебания:

а) возможный............. б: = 10 (xV/jn

б) уверенный............. £ = 50

Б) Затухающие колебания..... Е = 250

2) Радиотелефонный прием...... £ = 150

О нормах для радиотелеграфного автоматического приема см. Еыстродействиющие радиопередача и радиоприем и Атмосферные помехи. Для радиовещания большинство авторов дает следующие нормы из опыта: 1) наибольшая, определяющая наименьшее расстояние радиовещательной станции от окраины населенного центра Н. (в среднем) должна быть в 100 ООО И; при очень сильных местных помехах (в индустриальных центрах, в тропич. широтах) этот предел Н. может колебаться от 100 ООО до 1000 ООО [j-YIm []; 2) для т. н. площади А (в к-рой прием свободен от помех на 99% даже в случае расположения приемника в промышленном центре; иногда местные грозы и трамваи могут все л^е помешать) Н. доллсна быть больше 10 ООО [лУ/м; 3) для т. наз. площади В (в к-рой прием обычно свободен от помех, в деревенских или пригородных местностях; помехи появляются при установке приемника вблизи трамвайных проводов; атмосферные разряды вызывают перерыв в слушании

S S Москве

Врет ?чояса

г з 1 i 6 t S S ю II :s а tt 15 16 /ГУв i9 т'г'/УгЪг !

В среднем 5% общего времени передачи) Н. доллна быть в пределах примерно от 5 ООО доЮООО [iY/m; 4) длят. н. площади С (в к-рой получается прием, слегка страдающий от помех, но вполне доступный для слушателей в деревенских и полудеревенских местностях; атмосферные разряды вызывают перерыв в слушании в среднем 20% общего времени слушания, иреимущественно летом) Н. должна быть в пределах от 2 500 до 5 000 y-YJM Р]. Эккерслей тоже считает, что прием на кристаллический детектор (см.) при антенне 9 м гысотой, состоящей из 45 м провода, и хорошем заземлении возможен только на участках А и В .

Измерение Н. электрич. поля производится для слабых полей компараторами <см.), а в области сильных полей-рамкой

или опытной антенной, сила тока или напряжение в к-рых измеряется при помощи соответствующих термоамперметров или вольтметров [, На фиг. приводится для иллюстрации серия кривых Н. электрич. поля в Москве от радиостанции Туккертон (штат Нью-Джерсей, США, А = 16700 л*, расстояние от Москвы 7 600 км), измеренных лабораторией радиоприема Всесоюзного элек-тротехнич. ин-та аудиокомпаратором конструкции В. И. Баженова и А. И. Данилевского.

Лит.:) Reports of I. R.E.Committee on Broadcasting, Ргос. of the Inst, of Radio Eng. , N. Y., 1930, V. 18, I; 2) E с к e r s 1 ey P. P., Service Area of Broadcast Stations, ibid., 7; ) Б a ж e н о в B. И., Измерение излучения, ТиТбЦ , 1928, т. 9, 2 (,47) ш 4 (49); *)Б аженовВ.И. иСвистовН.К., Методы измерения напряженности электромагнитного поля и аудиокомпарирование, Вестниктеоретич. иэксперим. электротехники , М., 1928, т. 1, S; Б а ж е н о в В. Основы теории радиоприема, вып. 1, Москва, 1930; Б) Goldsmith А. N., Ргос. of the Inst, of Radio Eng. , N. Y., 1926, V. 14, 5.

НАРЕЗ KA винтовая, винтообразные выступы постоянных сечения и шага, расположенные на поверхности цилиндрич. или же слабо конических стержней (винтов) или отверстий (гаек). За исключением винтов, являющихся частью червячной передачи (т. паз. червяк, или бесконечный винт), винт всегда работает в соответствующей гайке, и поэтому вопрос о Н. сводится к определению тех условий, когда винт и гайка в совокупности наилучшим образом выполняют предъявляемые к ним требования. Подав-.ляюшее большинство винтов применяется в качестве скреплений; к Н. их предъявляют след. требования: 1) обязательное и надельное самоторможение; 2) прочность нарезки на изгиб и срезывание, не меньшая прочности самого тела винта на растяжение; 3) легкость изготовления Н. обычными применяемыми в машиностроении способами (преимущественно при посредстве метчиков, плашек и сродных им инструментов, реже на токарном станке); 4) возмолшо малое ослабление тела вийта как непосредственным уменьшением рабочего сечения его, так и путем создания острых входящих углов и резких переходов сечения, уменьшающих прочность винта; 5) возможность легкого кои-тро.лирования размеров. Этим условиям удовлетворяет всего лучше треуго.льная Н. с углом подъема 6°, с углом при вершине сечения Н., выбранным т. о., чтобы обеспечить выполнение 2-го и 4-го условий, с за-круг.лением на дне Н. достаточно большого радиуса и с прямолинейным очертанием верхней*части сечения нарезки (фиг. 1, А). К Н. винтов, передающих движение, предъявляют следующие требования: 1) возможно большой кпд, достигаемый путем увеличения угла подъема винтовой линии и уменьшения давления на опорные поверхности Н., 2) достаточная прочность Н. и ее жесткость во избежание появления нежелательных деформаций Н., 3) возможно малое ослабление прочности стержня винта; 4) возможно бо.лее равномерный и незначительный износ; 5) в нек-рых случаях возможность передачи усилий в обе стороны, иногда же лишь в одну; 6) легкая возможность точного изготовления. Следует установить различие между винтами, передающими гл. обр.