 |
 |
 |
 |
1 ... 27 28 29 30 31 32 33 ... 49 рий, NaaSiOs,-р астворимое стекло (в растворах называется также жидким стеклом), получаемое действием NajCOg или NaOH на SiOj. Все растворимые соли НаЗЮз легко гидролизуются (растворы показывают щелочную реакцию) и разлагаются не только сильными кислотами, но и угольной кислотой. Силикаты щелочноземельных и тяжелых металлов почти все нерастворимы и, будучи сплавленными в различных комбинациях, образуют стекло (см. Силикаты, Стекло). Кроме SiOg допускают также существование окиси кремния, SiO. Продукт такого состава получается восстановлением SiOa в электрической печи (в определенных условиях) и иод названием монокс (Мо-пох) употребляется в масляных красках и как абразионный материал. В чистом виде однако SiO не получена, и возможно, что монокс представляет собою смесь Si О*-Ь Si. Лит.: иПт. Enz., В. 10, 1922; Handb. d. anorg. Chemie, hrsg. v. R. Abegg, B. 3, Abt. 2, Lpz., 1909; B , B. 62, 1929. Б. Орионт. КРЕМОНА-МАКСВЕЛЛА ДИАГРАММА, см. Графическое определение усилий. КРЕН, наклонение судна около продольной оси, проходящей через центр тяжести площади грузовой ватерлинии. К, измеряется в градусах креномером (см.). Судно накре-нивается на один из бортов на угол (р при перемещении имеющегося на нем груза весом р (в т) в поперечн. направлении параллельно грузовой ватерлинии на I ж; угол (р находят из ф-лы (см. Остойчивость судов): где Q-поперечный метацентрическ. радиус, D-тоннаж судна в т, а-возвышение ц. т. судна над центром величины, т. е.над ц. т. погруженного объема. Для расчета небольших углов крена пользуются заранее вычисленной величиной момента, изменяющего крен на 1°. Судно кренится ташке при повороте, качке, бортовом залпе, на ходу под парусами; наибольшей величины крен достигает при аварии и затоплении отсеков. Значительный К. ухудшает мореходные качества судна и вызывает опасность опрокидывания. Большой постоянный крен выравнивается затоплением специальных отсеков (противокренных) или целых отделений судна. Р. тншбвйн. Лит.: см. Цифферепт. КРЕНОМЕР, прибор ДЛЯ определения угла наклонения судна около продольной оси (см. Крен). Статические приборы (отвес, уровень, визир, квадрант) при качке непригодны, так как дают в этом случае неверные показания и не позволяют поверить отсчет. Простейший К.--короткий маятник, заключенный в застекленную металлическую коробку со шкалой, показывающей углы крена в градусах. Динамич.К.-фотовизирные,маятниковые, жироскопические. Простейший креномер без записи-уровень со специальным устройством для замедления движений пузырька воздуха []. Линиодиаграф Хьюса [2] фотографич. аппарат (см. фиг.) с двумя объективами 1 и 2, оси которых (под углом 90°) устанавливаются перпендикулярно и параллельно борту; камера снабжена переборками 3; пленка 4, передвигаемая часовым механизмом, закрыта пла-  стинкой с узким вертикальным прорезом 5. Фотографируя видимый горизонт, получают полоски с пограничной (море-небо) черточкой, к-рые, сливаясь, дают кривую амплитуды размахов; для измерения на пленке наносится масштаб длины и времени; угол крена ср будет: tg(p=a:f, где а - амплитуды на пленке, / - фокусное расстояние. Прибор регистри рует одновременно бортовую и килевую качку; его недостатки-громоздкость, кратковременность наблюдений, зависимость от погоды. Прибор Бертепа имеет два маятника: 1) тяжелый обод, наса-л^енный эксцентрично на ось, с большим периодом и 2) сплюснутый конус с малым периодом и воздушным демпфером. Отличие периодов маятников от периодов корабля и волн позволяет при помощи отметчиков наносить на бумагу отклонения от вертикали (первым) и нормали к волне (вторым) Р]. Прибор Комментра имеет только маятник второго тина [*], прибор В. Ф р а уд а-только первого Недостаток этих приборов-склонность к резонансу, к-рый однако легко исключается из диаграммы. Жироскопич. приборы наиболее удобны, имеют тяжелый жироскоп, подвешенный горизонтально на кардане с самопишущим устройством. Прибор Фрама [ ] пригоден для продолжительных наблюдений; прибор Петравик и К (Вена) действует недолго, но отмечает килевую и бортовую качку. Активный жироскоп С п е р р и [] сходен с предыдущими. Влияние резонанса невелико. Лит.: ) Schiffbau-Kalender, Berlin, 1925, p. 589; ) Jahrbuch d. Schilfbautechnischen Gesellschaft , Berlin, 1910, p. 707; ) Крылова. H., Теория кренометра, Записки по теории корабля, стр. 178, СПБ, 1900; *) Comment z, Krangungs-Messer, eWerft, Reederei, Hafen , В., 1924, 22 Okt., p. 520; ) F г о u-d e W., Description of an Instrument for Automatical-Iv Recording the Rolling of Ships, Trans. of the Inst, of Naval Archit. , L., 1873; Jahrb. d. Schiff-bautechn.Gesc]lschaft ,B., 1911,p. 341; ) J о h о w s, Hilfsbuch fiir d. Schiffbau, 5 АнП., В., 1928, p. 433; ) Transactions of the Society of Naval Engineers*, New York, 1915. P. Тншбвйн. КРЕОЗОТ, продукт перегонки тяяселого масла, получающегося из смолы букового дерева (см. Дерево, сухая перегонка). По составу креозот представляет собою смесь свободных фенолов и метиловых эфи-ров двуатомных фенолов, кипящую в пределах 200-220°.Креозот-бесцветная или слабожелтая, сильно преломляющая свет жидкость, жгучего вкуса, с характерным пригорелым острым запахом, при 20° сиропообразная, но не застывающая; уд.в.1)дб1,075. При растворении в 120-150 частях воды при 15° К. дает мутный раствор, в кипящей воде-прозрачный; со спиртом, эфиром, бензолом, нефтяным бензином, сероуглеродом и уксусной кислотой смешивается в любых отношениях. В алкогольном растворе 1 :4 с хлорным железом К. сначала дает муть, затем голубое окрашивание, быстро переходящее в серо-зеленое и далее в грязно-коричневое, с выделением такого же цвета хлопьев (реакция на гваякол). Бромная во- да с водным раствором К. выделяет красно-бурый осадок. К. растворим в слабых растворах щелочей. На воздухе он горит сильно коптящим пламенем. К. обладает высокими иротивогнилостными и противобродиль-ными свойствами (дым, получающийся при горении дерева, своей консервирующей способностью обязан присутствию К.); он свертывает белки и раздражающе действует на кожу и слизистые оболочки. В состав К. входят: гваякол, СвН4(НО)ЧСНзО)2 (50-60%), креозол, СвНз(СНз)ЧСНзО)ЧНО)4, тг-крезол, СбН4(СНз)ЧНО)*, флорол, С,Я,(С,и,У(иОГ', ксиленолы, СвНз(СНз)2(НО), и пирогаллол-диметиловый эфир, CsHsiCUaO) >\и0У; далее-метилпирогаллолдиметиловый эфир, СвН2(СНз)(СНзО)2(НО),ипропилпирогаллол-диметиловый эфир, СвН2(СзН7)(СНзО)2(НО). Для получения К. смолу букового дерева, содержащую его до 5%, подвергают перегонке и фракцию, кипящую при 150-250°, суд. весом > 1 (т. н. тяжелое масло) обрабатывают едким натром для извлечения фенолов и к-т. Осветленный раствор разлагают серной кислотой, снова обрабатывают едким натром с последующим разложением серной кислотой, повторяя эту операцию до тех пор, пока не получат продукта, нацело растворяющегося в едком натре и дающего совершенно прозрачный раствор. По разложении прозрачного щелочного раствора серной кислотой всплывший на поверхность маслянистый слой сырого К. отделяют, промывают слабым раствором едкого натра, осторожно перегоняют и отбирают фракцию, кипящую при 200-220°. В настоящее время предложено много других методов выделения К. из сырого тяжелого масла. Для удаления к-т и выделения фенолов применяется например обработка магнезией, или л-се сырое масло-непосредственно или после разделения на фракции, кипящие нри различных t°,-обрабатывают конц. соляной к-той под давлением. Чтобы получить совершенно чистый К., имеющий удельн. вес D,5 = 1,08 и растворяющийся 6ie3 остатка в слабых гцелочах, приходится многократно обрабатывать сырой К. слабыми растворами едкого натра, продувать щелочной раствор паром (для освобождения от суспендированных маслянистых частичек) и по выделении К. к-той многократно перегонять его в медном кубе с термометром, причем первые перегонки обычно ведут с применением медного холодильника, последняя же дистилляция производится с серебряным холодильником. Трудность получения креозота в чистом виде зависит от присутствия в нем, помимо фенстов и их производных, некоторых веществ (главным образом углеводородов), не реагирующих со щелочами, но в присутствии фенолов растворяющихся в них, чем и обусловлена необходимость повторных обработок щелочами и кислотой. К. применяется в медицине и санитарии как дезинфекционное средство. Он является также исходным веществом для получения ряда патентованньгх лечебных средств; сюда относятся продукты конденсации креозота с к-тами: фосфорной, валериановой, масляной, камфорной и дубильной; помимо того применяются таклсе соединения креозота с уксуснокислой ртутью и продукты уплотнения его с формальдегидом. В технике гораздо большее значение, чем древесный К., имеет К., получаемый из каменноугольного дегтя,-так наз. креозотовое масло. Среди жрщких продуктов перегонки каменноугольного дегтя креозотовое масло относится к наиболее высоко-кипящим фракциям (при t° от 150 до 400°). Обычно при получении креозотового масла отбирают фракции, к-рые кипят в пределах 220-300°, причем допускается не более 10% продуктов, кипящих ниже 235°. Креозотовое масло имеет уд. вес Di5= 1,03-1,10; содержит нафталина не более 5% (немецкие сорта) или 10% (русские) и от 8 до 10% высших фенолов и нафтолов, растворяющихся в едком натре. Высшие фенолы, вплоть до тетра- и пентаметилфонолов, являются наиболее ценной составной частью креозотового масла; кроме того в нем присутствуют азотистые основания ряда пиридина и хинолина, а таюке и гетероциклические азотистые продукты, как карбазол и инден. Креозотовое масло в технике считается лучшим из антисептических средств, в особенности для предохранения дерева от гниения. Пропитанные им сосновые шпалы вы-дерлсивают от 20 до 30 лет слулбы, тогда как без такой обработки они приходят в негодность через 7 лет; пропитанные им телеграфные столбы держатся до 50 лет. В настоящее время годовое потребление креозо-топого масла превысило 3 500 т. На бензольны :с заводах креозотовым маслом пользуются в качестве поглотительного масла для орошения скрубберов и улавливания легких углеводородов; его применяют таклсе для извлечения уксусной кислоты из лсидких продуктов сухой перегонки дерева. Употребляемые для этих целей дистиллаты подвергаются более тщательн. очистке, чем шпалопропиточное креозотовое масло: они д. б. освобождены от нафталина, антрацена и других твердых составных частей и должны оставаться жидкими при низких t°. При сухой перегонке дерева креозотовое масло применяют в качестве катализатора, предварительно обрабатывая им древесную стружку, что ведет к увеличению выходов метилового спирта; особенно сильное катализирующее действие достигается при ведении сухой перегонки под давлением. Наконец креозотовое масло находит применение в качестве топлива для котельных и для двигателей внутреннего сгорания; как жидкое горючее оно уступает мазуту, обладая меньшей теплотворной способностью. Лит.: Пантелеев В. П., Сухая перегонка дерева, М., 1920; Козловский П., Сухая перегонка дерева, М., 1906; Фокин Л. Ф., Обзор химическ. промышленности в России. Каменноугольная смола, ч. 2, вып. 1, П., 1922; В и gg е Ст., Industrie d. Holzdestillationsprodukte, Technische Fortschrlfts-berichte, hrsg. v. B. Rasso-w, B. 15, Dresden-Leipzig, 1927; Ullm. Enz., B. 7; Meyers Lexikon, 7 Auflage, B. 7, Lpz., 1927; Chemische Technologic d. Neuzeit, herausgegeben v. O. Dammer, B. 5, Stuttgart, 1925; Hagers Handbuch d. Pharmazeutischen Praxis, B. 2, Berlin, 1929. B. Kapacei. КРИВОШИП, часть кривошипного механизма (см.), являющегося в свою очередь частным случаем четырехзвенного шарнирного механизма. Практическое вьгаолиепие кривошипа-см. Коленчатые вали. КРИВОШИПНЫЙ МЕХАНИЗМ, частный случай четырехзвенного шарнирного механизма, или шарнирного четырехугольника/ Четырехзвенный шарнирный механизм представляет собой шарнирный четырехугольник OiABO (фиг. 1). Не-подвижньв! может быть любое из четырех его звеньев, причем в зависимости от соотношений длин звеньев могут представиться следующие частные случаи: 1) два звена  s7 7  Фиг. 2. могут описывать полные окружности-дву-кривошииный механизм (фиг. 1); 2) только одно звено может описывать полную окружность, а третье (коромысло) описывает лишь дугу окружности-кривошипно-коромыс.то-вый механизм (фиг. 2); 3) ни одно звено не описывает полной окрулшости-двукоромы-словый механизм (фиг. 3). Если обозначить длину самого короткого звена через г, средних по длине-R и I и самого длинного буквой L, то, согласно теореме Грасгофа, если r + L<R-\-l, т. е. если сумма длин самого короткого и самого длинного звеньев меньше, пендели сум' ма длин двух средних звеньев, то механизм д в у к р и в о ш и пн ы й, когда неподвижно самое короткое звено, и к р и-вошипно-коро-м ы с л о в ы й, когда неподвижно звено, см еловое с самым коротким. Если r+L> R+1, то механизм двукоромы еловый. Если г=RkL=l, причем равные звенья не смежны, то шарнирный четырехугольник превращается в шарнирный параллелограм, часто применяющийся (в паровозах) для передачи вращения параллельным валам (фиг. 4). Если кривошипы все время параллельны друг другу (спарный механизм), то передаточное число равно 1; шатун АВ тогда часто называют спарником. Если равные кривошипы О^А и Оа-В не параллельны друг другу, то вращение их происходит в обратные стороны, и механизм называется шарнирным антипараллелограмом, или антипараллельными кривошипами (фиг. 5); передача двюкепия в  Фиг. .3.  Фиг. 4. Фиг. 5. этом механизме происходит с переменным отношением скоростей, изменяющимся по такому же закону, как в тождественных эллиптич. зубчатых колесах, оси вращения которых совпадают с фокусами начальных  Фиг. 6. ЭЛ.71ИПС0В. Если же равные по д.лине звенья смежны, то получаем механизм шарнирного равнобочника (фиг. 6); если в нем неподвиншо одно из коротких звеньев, то короткий кривошип может делать два оборота, , в то время как длинный i j.; кривошип делает один Т оборот; если неподвиж- но длинное звено, то короткий кривошип также может описать два оборота, в то время как коромысло сделает одно полное качание. Крайние положения В'о и В„ шарнира В коромысла называются его мертвыми точками; для нахождения мертвых точек засекаем (фиг. 2 и 3) из Орадиусами OiA+AB и АВ - О^А, а из 0 радиусами О^В+АВ и АВ- О^Вдуги до пересечения с соответственными траекториями. Отсутствие точек пересечения показывает, что данное звено не имеет мертвых точек; па фиг. 2 и 3 мертвые точки обозначены соответственными буквами с индексом 0. В частном случае, когда центр 0 криво-шиппо-коромыслового механизма (фиг, 2) удален в бесконечность, точка В получает прямолинейное поступательное движение; заменив коромысло О^В кинематически эквивалентной парой скольжения, получим К, м. На фиг, 7 представлена схема центрального К, м., со- ,.-9Zj стоящего из кри- ; вошипа 1 (ОА=г), \  Фиг. 7. шатуна 2 (АВ=1), ползуна 3 и стойки или неподвижного звена 4. Механизм назван центральным, так как прямая линия ВХ, по которой двюкется геометрическая ось шарнира В, своим продолжением проходит через точку о, В противоположном случае будем иметь нецентральный К, м, В машиностроении применяются также многие преобразования этого механизма, составляющего главную часть поршневых двигателей и насосов. Если например увеличивать радиус цапфы А или уменьшать радиус кривошипа OA настолько, что радиус цапфы станет больше суммы радиусов кривошипа и шейки коренного вала О, то получим механизм эксцентрика. Если вместо ОХ стойкой сделать звено АВ, то получится механизм старой пароходной машины с качающимся цилиндром. Если сделать неподвижным звено OA, то получится механизм воздухоплавательного двигателя Гном с вращающимися цилиндрами и т. п, Кинематич. исследование механизма фиг.7 м.б, вынолнено аналитически и графически. Если обозначить отношение длин кривошипа и шатуна через А = г: I и искать расстояние OiB=x точки В от среднего ее положения 0, воспользовавшись разложением квадратного корня по бинол1у Ньютона, то [/л , ЗЛ , , \ , /Я , Я , О^-(4 + 1Г + Г024 +-) + (4 + Гб + + + ...)cos2-g + gl+...)cos 4?.+ + (5°, Н----) cos Q<p- ... Величина х выралсается бесконечным рядом Фурье по четным косинусоидам, причем амплитуды представляют собою быстро сходящиеся алгебраические ряды от дробной величины Д; обыкновенно As 0,2, поэтому во многих случаях допустимо пользоваться сокращенным рядом. В самом грубом прибли-жешш x = rcosq}, т. е. пстожение ползуна и поришя определяется проекцией цапфы кривошипа А. Более точно х=г COS 93 - (1 - COS 2<р). Для (р = 0, ж=+г; для (р^180°, х=-г, т. е. ход ползуна и поршня S = 2r; для 9? = 90°, ж= - - J т. е. на взмахе поршень не находится в среднем положении. . Графически иололсения ползуна легко находятся засечками; иногда пользуются биполярной диаграммой проф. Ф. А. Брикса. При вычерчивании в большом масштабе рекомендуется следуюхцее построение (фиг. 8): проводим из центра О окружность радиуса г и размечаем ее Точками i, 5 и т. д.; через центр Опрово- У vl-~---- -ДИМ дугу 0Y окружности, радиус к-рой равен I и центр которой расположен на ОХ; горизонтальные ..... , Д....... расстояния точек 1, 2 и т. д. до этой дуги равны х; откладывая i ОС=х по ОХ, раз- Фиг. 8. мечаем пути ползуна. Если нужно кроме того знать положение линии АВ шатуна, то строим при точке А угол ВАС = ХСА (точка С изображает положение ползуна, которое соответствует углу поворота кривошипа ХОА). Если кривошип вращается равномерно, делая п оо/мин., то (p = (at (где ш= . -угловая скорость кривошипа). Производная от х по времени определит тогда мгновенную скорость ползуна + ...)sin4a) -g + ...)sin6a)f-f...]. В самом грубом приближении г! =-гсо sintof, во втором приближении со sin -Ь i sin 2mi. Для графического построения мгновенной скорости ползуна (фиг. 7) продоллсаем АВ до пересечения с линией OZ LOX в точке тогда ОУ Х> = Г(Х>- -  ~ \16 ~ 64 Т. е. отрезок OF изображает скорость ползуна в том масштабе, в каком отрезок OA изображает скорость пальца кривошипа гсо. На фиг. 8 указано то же построение в большем масштабе. Для определения ускорения j ползуна проводим 1Ш точки V линию VE параллельно ОХ до пересечения с продолжением 0J.;n3 Е - линию EF параллельно 0Z до пересечения с АВ пли его продолл^:ением и из F- линию FI перпендику.1ярно АВ до пересечения с ОХ. Отрезок 01 изображает ускорение ползуна в том лее масштабе, в каком отрезок OA изобралсает tojt-. Аналитически ускорение находим как производную скорости по времени dT -to--cos cof-(Я+ + -~ -f j cos2(uf+ + (f 4+---)cos4a, -(-f...)cos6fo +--]. К. м., как и всякий четырехзвенный, имеет 6 мгновенных центров, из к-рых 4 представляют собой сами шарршры: Z = 0; = = А\ Zag/?; 2з4леж;ит в бесконечности в направлении, перпендикулярном к ОХ; пос-троепие мгновенного центра показано на фиг. 7; Zi3 = F. Если задана сила Р, действующая на поршень по линии его двилеения, то легко построить эквивалентную касательную силу К, приложенную в А перпендикулярно к OA: К=Р Для построения (фиг. 7) откладывают АМ~ =Р, проводят MN параллельно 0Z и получают MN=K. Силы инерции К. м. обыкновенно находят приблилгенно по весу звеньев, двилеущихся прямолинейно - поступательно (поршня, штока, ползуна), причем для обоб-ш:ения результата и сложения с давлениями пара относят вес к 1 см шлощади поршня; кроме того к найденному выше весу прибавляют егце 0,3 - 0,45 веса шатуна, разделенного также на площадь поршня в см; умножая полученный вес q кг/см на мгновенное ускорение поршня j и изменяя направление на обратное, получают си.чу инерции возвратно движущихся частей Ъ = а кг!см , где fir=9,81, если j в м/ск. Существует несколько методов точного построения силы инерции шатуна; нек-рые из них описаны в приведенной ниже литературе (см. таклсе Динамика поршневых двигателей). Лит.: 3 е р II о в Д. С., П1)икладнап механика, Л., 1925; С м н р н о в Л. П., Кинематика механи.з-мов и машин, М.-Л., 1926; Б р и к с Ф. А., Эксцентриковое парораспределение с учетом конечной д.лп-пы шатуна и эксцентриковых тяг, Москва, 1928; Рерих К. о., теория регулирования машин, ч. 1, Маховое ко.пссо и периодическая неравномерность вращения матпин, П., 1916. К. Рерих. КРИВЫЕ. Для и.зучения свойств кривых математика пользуется методом координат. Задание К. равносильно заданию уравнения, связывающего прямоугольные координаты точек К. Уравнению кривых (в декартовых координатах) можно придать различные формы: у = f(x) или F{x, у) = О или же ж = 99(f), у = y}[t) (см. Дифференциальная геометрия), причем оследняя форма является в теоретических исследованиях и теоретической ме- ханике предпочтительной, так как она устанавливает равноправность координат х я у. В некоторых случаях вместо уравнения К. в декартовых координатах выгоднее бывает рассматривать ее уравнение в криволинейных координатах, чаще всего в полярной системе (см. Координаты). Здесь ур-ие К. дается в виде связи между радиусом-вектором q и полярным углом (О : Q = f((o) или Ф(о, со) = 0. Но к.тассификация кривых проводится по их ур-иям в декартовых координатах. Если левая часть ур-ия F(x, у) = 0 есть целая рациональная ф-ия X и у или м. б. приведена к такому виду, то соответствующая кривая называется алгебраической и порядком кривой называется степень этой целой рациональной функции. Если же функция F(x, у) содержит в себе знаки трансцендентных операций, то кривая F(x, у) О называется трансцендентной. Первый вопрос при изучении кривых-вопрос об установлении ее формы. При этом большую пользу приносит знание расположения ее замечательных точек и положение асимптот. К замечательным точкам относятся точки перегиба, точки прекращения, точки с вертикальными и горизонтальными касательными и особые точки. Главнейший вид особых точек К.-к ратные точки, в которых К. пересекает сама себя. Простейший пример кратной точки - двойная точка. Координаты двойной точки определяются как общие решения трех ур-ий: F(x, 2/) = О, дх ду Если эти три ур-ия имеют общее решение ж', у', то точка с координатами х', у' и будет особой точкой; две касательные в двойной точке определяются из ур-ия: У = У' в зависимости от знака двучлена \дхду) 9x2 эти касательные действительны и различны при ЛуО (фиг. 1), мнимы при Л <0 (фиг. 2) или действительны и совпадают при zl=0 (фиг. 3). в первом случае особая точка есть узел, во втором - изолированная точка и в третьем-точка возврата. Если в точке (ж', у') обращаются в нуль все частные производные от F до порядка к-1 включительно, то имеем /с -к ратную точку. В этой точке пересекаются к ветвей К., и касательные к ним даются ур-ием: ,(1-ж')Ч- Точки перегиба находят из ур-ия = / (ж) = 0, если уравнение К. имеет вид: y=f(x). Для К., заданной ур-ием (ж, у)0, точки пе- региба определяются совместным решением следующих двух уравнений: F(x и)~0 (Y-l-(.4-Y-О т Координаты точки, в которой касательная параллельна оси ОХ, определяются из уравнений: F = 0, = 0; точки с касательными, параллельными оси 0Y,находятся из уравне- НИИ F = 0, = 0. Большую услугу оказывает далее знание полож:ения асимптот (см. Асимптотическое приближение). Приложим эти общие сообраладния к исследованию некоторых К. Рассмотрим д е-картов лист (фиг. 4): (ж, у) = жз + у^- Заху = 0. Эта кривая-алгебраическая 3-го порядка. Уравнения = Зж-Зй2/ = 0, If = 32/-Заж = 0, F = жз -{- ?/з - Заху = О имеют общее решение: ж=0, у = 0. Найдем затем: V = о у = о поэтому zl = 9ft>0, следовательно декартов лист имеет в начале координат узел. Касательные к ветвям узла можно найти из уравнения (2), принимая во внимание (4); получим: = О, т. е. оси координат будут являться касательными к кривой в узле. Правила для определения асимптот алгебраических кривых указывают, что декартов лист имеет одну асимптоту и ее ур-ие: ж+ + а=0. Этого исследования достаточно, чтобы установить вид К. Применим те же рассмотрения к конхоиде. Конхоидой называется геометрич. место точек, для которых часть MP радиуса-вектора ОР, заключенная между точками М и Р, равняется данной величине I, причем точка М прхшадлежит постоянной прямой А А' (фиг. 5). Отсюда ур-ие конхоиды: Ен(у- ау- (ж2 -Ь у') - Ihf = 0. (5) Прямая АА имеет ур-ие у = а. Т. о. конхоида-алгебраич. К. 4-го порядка. Найдем ее особые точки; совместное решение уравнений (1) показьшает, что начало координат-двойная точка кривой. Она будет узлом (фиг. 5), ести А = 4а^ (Р - а2) > О, при А <0 она будет изолированной точкой (фиг. 6), при J =0-точкою возврата (фиг. 7). Уравнение (2) здесь примет следующий вид: V W-a Решая ур-ие F=0 относительно ж, найдем: -Г (у-а)2 следовательно при t/=a, ж=оо и прямая 2/=а будет асимптотой конхоиды. Уравнение (5) содержит лишь четные степени ж, а потому конхоида симметрична относительно оси 0Y.  А<0 Фиг, 2.     Фиг. 5. Фиг. 8. Фиг. 10. Фиг. II.  Фиг. 3. Фиг. 4.
Фиг. 6. фиг. 7. 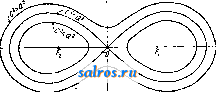   Фиг. 15. Фиг. 13.

Фиг. 16. Фиг. 17. Все эти свойства конхоиды позволяют установить ее внешний вид. Конхоида была введена греческим геометром Никомедом для решения задачи о трисекции угла. Овалы Кассини введены астрономом Кассини для решения одной механической задачи (частного случая задачи о трех телах). Характеристическое свойство этих К.: произведение расстояний произвольной точки кривой до двух данных точек, фокусов Fi и jPg* есть величрша постоянная с^. Обозначим расстояние мелсду фокусами через 2а и поместим их на оси ОХ симметрично относительно точки О. Тогда уравнение овала Кассини будет: F З(ж2 + у^У - 2а^ (ж2 у^) - 4 (.4 = О, (6) Это уравнение показывает, что овал Кассини симметричен и относительно оси ОХ и относительно оси 0Y. Легко видеть, что овал Кассини не имеет ветвей, уходящих в бесконечность, и т. к. его уравнение avTre6pan-ческое, то он является замкнутой К. Ур-ия не имеют при сфа общих решений, т. е. овал Кассини не имеет особых точек. При с^=а^ эти уравнения имеют общее решение ж=0, у=0; начало координат будет узлом; К. имеет характерный вид восьмерки. Эта кривая известна под именем лемнискаты Б е р и у л л и. Ее ур-ие в полярных координатах: g2 = 2a2 cos2(p. Если рассмотрим всю совокупность кривых Кассини для изменяющегося сто установим, что при с^>а^ овал Кассини представляет одну замкнутую кривую; при уменьшении с этот замкнутый овал, переходя через лемнискату, распадается на две отдельные замкнутые К. (фиг. 8). Рассмотрение трансцендентных К. начнем с весьма известной кривой-циклоиды. Циклоидой наз. К., описываемая произвольной точкою Р круга при его качении (без скольжения) по прямой ОХ. Пусть радиус круга будет R, а расстояние рассматриваемой точки до центра круга С будет Ь. Тогда уравнение циклоиды будет: x=R(p - b&in(p, у = R - b cos (р. Если b = R, то мы имеем нормальную циклоиду; она представляет собою бесконечное число арок, соединенных между собою в точках ж = 2я fc(/e = 0. ± 1, + 2,...); эти точки-точки возврата циклоиды (фиг. 9). При Ь> R имеем удлиненную циклоиду; она обладает бесконечным числом уз.тов (фиг. 10). При Ь <R, получаем укороченную циклоиду; она не обладает особыми точками (фиг. 11). Непосредственным обобщением циклоиды являются гипоциклоиды и эпициклоиды: кривые, описываемые точкою Р одного круга при его качении но другому кругу. Если радиус первой окрулшости назовем через г, а радиус второй, опорной, окружности через R и покатим первую окружность по внешней стороне второй, то будем иметь следующее уравнение эпициклоиды (фиг. 12): При качении по внутренней стороне получаем гипоциклоиду (фиг. 13): х = (R-r) cos q} -\-h cos ((ру, y=(R-r) sin9? - Л sin y;. x-= (R + r) cos<p- h cos {(ру, у = (R + r) sin 9? - h sin (- ?) Здесь через h обозначено расстояние рассматриваемой точки до центра катящегося круга. Форма гипо- и эпициклоид существенно зависит от арифметического характера отношения -; ири - рациональном кривая представляется замкнутой; кроме того в этом случае наши кривые алгебраические. При иррациональном у кривая обладает тем замечательным свойством, что, какова бы ни была точка М внутри кольца ж2 + 7f - = о, x + y-(R± rf = О и как бы ни был мал радиус нек-pdro круга у с центром в точке М, всегда найдется бесконечное множество точек гиноциклои-ды (эпициклоиды), лежащих внутри этого круга у. Рассмотрим некоторые частные случаи. 1) jR = 2r и h-произвольно. Урш (7) дают эллипс. На этом свойстве основано устройство нек-рых эллипсографов. 2) R=r. Ур-ия (7) дают после исключения <р, замены координат x=x-\-h и перехода к полярным координатам: Q = 2(r - h cos oi); эта К. носит название улитки Паскаля (фиг. 14 а, 14 6). При h=r имеем кардиоиду (фиг. 15): е = 2г (1 - сов со). 3) R = 4r и /t = r. Уравнения (7) дают астроиду (см.) (фиг. 16): Задача о гипоциклоидах и эпицик.11оидах мол№т быть обобщена на две произвольные кривые Г и Г' рассмотрением пути произ-вольн. точки кривой Г, катящейся по кривой Г'. Составление ур-ий соответствующей К., при произвольных Г я Г', осложняется необходимостью знать выражения длин дуг К. Рассмотрим теперь цепную линию: = (е -Ье ); 2/ = она представляет собою фигуру равновесия тян^елой гибкой и перастяжимой нити. Если в какой-нибудь ее точке М провести нормаль до пересечения 6 осью ОХ, то отрезок MN будет равен радиусу кривизны цепной линии в точке М (фиг, 17). Если далее из точки Р опустить на касательную МТ перпендикуляр Рт, то отрезок Mm будет равен длине S дуги цепной линии от точки А до точки М. Геометрич, место у точек т представляет собою эвольвенту цепной линии. Можно доказать, что тР сохраняет постоянное значение для всех точек М цепной линии. Кривая у есть трактриса. Длина S цепной линии от А до М имеет следующее выражение: s = (ef-e ); 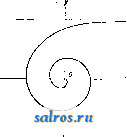 Фиг. 18. отсюда уравнение трактрисы будет: Xi = а COS 0 + а In tg . У1= а sin в. Трактриса имеет в точке А точку возврата и ось ОХ своей асимптотой. К семейству трансцендентных К. принадлежат и спирали. Под спиралями понимаются обычно К., делающие бесконечное число оборотов около какой-нибудь точки. Простейшим примером служит архимедова спираль (см.): Более слолсные примеры дают г и и о р-б о л и ч е с к а я спираль (фиг. 18): г = - , и л о I а р и ф м и ч е с к а я спираль: г= е . Гиперболическая спираль обладает следуюпщми свойствами: оиа имеет асимптоту /= /с, к которой приближается при (р^О,я имеет далее точку (0,0) в качество асимптотической точки. Характерным свойством ло-гарифмич. спира.ти является ее неизменяемость при преобразовании подобия с центром в точке О. К разряду спиралей относятся и к р ив ы е Ф р о н о л я, встречаемые в теории диф-фракцни (см. Диффращия): о о Хотя входяище сюда квадратуры взять и невозмол-аю, но можно тем не менее составить представление о форме К. При s -Ь оо К. делает бесконечное число оборотов около ТОЧКИ (-- , -,-J, а прп - оо она делает бесконечное число завитков около точки / аУ л. а|лг\ \~ 2~ 2 / Тригонометрические К.-см. Тригонометрические функции. Лит.: г у р с а Э., Курс математического анализа, т. 1, м., 1911; j: г о р о в Д. Ф., Дифференциальная геометрия, м.-П., 1924; Loria С, Spuziclk! algebraLschc und transzendente ebene Kurven. 2 Aufl., Bd. 1, 2, Lpz.-в., 1910-1911; W i e 1 e i t n e r H.. Tlieorie d. ebcncn algebraischrn Kurven bohcrer Ord-nung, Berlin, 1905; Hilton H., Blano Algebraic Curves, Oxford, 1920. Л. Сретенский. КРИОЛИТ, фтористый натрий-алюминий, AlFg 3 NaF, минерал моноклинной сипго-нии. Кристаллы редки и по б. ч. мелки. Излом раковистый, хрупок, тв. 2,5-3, удельн. вес 2,95-3; цвет снежнобелый, реже-красноватый, буроватый, далее черный, но б. ч. бесцветен, водянопрозрачен. Блеск стеклянный, жирноватый, на плоскостях спайности перламутровый. Плавится весьма легко (975° по Мольденгауеру). Растворяется в серной кислоте с выделением HF. Встречается весьма редко. Обыкновенно залегает сплошными массами, а таклсе в крупнозернистых агрегатах, вместе с железным и медным колчеданами, свинцовым блеском, железным шпатом и квар7:1вм. Наибольшее промышленное значение имеет месторолсдение Ivigtut на западном побережьи Гренландии, у фиорда Arsuk. Здесь К. залегает в виде жилы (ок. 180 в длину и 30-55 м в ширину) в гранитном массиве, лежащем в гранито-гнейсе. Запасы К. здесь значительные.Точных данных о запасах нет. В СССР на Урале (близ Миаса) было встречено небольшое гнездо К. в жиле альбито-вого гранита; в Америке (Колорадо, около Pilces -Peak) имеется месторождение криолита непромышленного характера. К. применяется в качестве плавня при электролитич. получепии алюминия; окись алюминия легко растворяется в расплавленной двойной фтористой соли алюминия и натрия (К.-AlgFg- 6 NaF). Кроме того К. применяется в стекольной промышленности для получения молочного стекла и в производстве эмали для железных и фаянсовых изделий. Небольшое количество идет в качестве плавил при литье меди и в нек-рых других производствах. Заменителем К. в керамической промышленности является кре-мнефтористый натрий. В последнее время природный К. повсе^ местно заменяется искусственным К., к-рый приготовляется (на алюминиевых заводах) действием плавиковой к-ты на чистую окись алюминия и соду; в свою очередь плавиковая к-та получается действием серной к-ты на чистый фтористый кальций. Реакция образования двойной соли фтористого алюминия и фтористого натрия (искусственного криолита) представляется ур-ием: AI2O3 + 3Na2C03 + 12HF = AlaFe 6 NaF-b3C02+6H20. Применением искусственного К. в очень чистом виде достигается получение чистого алюминия. На опытном з-де Ин-та прикладной минералогии выработан способ искусственного получения криолита. В основе этого способа лежат следующие реакции: в 10- 15%-ной плавиковой к-те растворяется необходимое количество AlgO., (г.тинозем) для получения кислой соли AlFg-SHF, которая вместе с содой превращается в К.: 12 HF + AI2O3 = 2 (AIF3 3 HF) + ЗН2О; 2(AlF3-3lIF)+3Na2C03=2(AlF3-3NaF)-b3C02-l-3H20. Осалсдение К. производится в чанах, выложенных свинцом; содержание воды в свеже-осажденном К. доводится при посредстве фильтр-прессов до 30-40%, после чего К. окончате.тьно просушивается в обогреваемой при помощи топки вращающейся печи (сушильный барабан). Вывоз, ввоз и средние цены на п р ир о д н ы й к р и о л и т.
Растворитель Торговля естественным К. сосредоточена в руках датских концессионеров (месторол-дение Ivigtut принадлежит Дании). Вывоз и средние цены на природный К. указаны в таблице, помещенной выше. Цены на сырой К. держались в среднем ок. 50,35 долл. за т. Цена чистого К. около 100 долл. за т. Потребность СССР в К. удовлетворялась лишь ввозом. Лит.: К у р д 10 м о в А. П., К вопросам создания в России алюминиевого производства, Труды Ин-таприкл. минер, и металлургии , М., 1923, вып. 6; Федоровский Н. М., Минералы в промышленности и с. х-ве, 2 пзд., Ленинград, 1927; В а 1 d а н f, t}ber d. Kryolithvorkommen in frronland, Ztschr. fiir prakt. ri(!ologie , Halle a/S., 1910; Dammer B. und T i e t z e O., Die nutzbaren Mineralien, Kryolith, mit Ausnahmc d. Erze, Kalisalze, Kohlen und d. Petroleums, В. 1, Stg., 1928; Davis H. W., Fluorspar a. Cryolite in 1926, Min. Res. of the U. S. Geolog. Survey , Wsh., 1927; Gordon S., Mining Cryolite in Greenland, <.Eng. and Min. Journ. , New York, 1926, Febr., p. 5; Grunwald J., Chem. Technologie d. Emailrohmaterialien, В., 1922; L ad о о R., Non-metallic Minerals, p. 176, N. Y., 1925. H. Федоровский. КРИОСКОПИЯ, учение об определении мол. в. растворенных веществ по понижению ими точки замерзания чистого растворителя. Вместе с эбуллиоскопией (см.)-определением мол. в. по повышению точки кипения- К. является наиболее употребительным и точным методом определения мол. в. веществ в растворенном состоянии. Понижение точки замерзания t раствора сравнительно с точкой замерзания to чистого растворителя-д е п р е с-с и я At = tf,- t, вызывается тем, что давление р пара раствора понижено по сравнению с давлением Ро пара чистого растворителя (Ар = Ро - Р > 0), т. к. в точке замерзания давления пара раствора и вымерзающе- -го чистого растворителя д. б. одинаковыми. Термодинамически можно показать, что депрессия At, как и понижение давления пара Ар, для слабых растворов пропорциональна концентрации с в г-молекулах на 1 ООО г растворителя: At = ко - с (1) (1-й закон К.); при с=1, At = ko; поэтому ко называется молекулярной депрессией; ко зависит только от свойств взятого растворителя. 2-й закон К. определяет величину ко. Qo 1000 ~ с [R - газовая постоянная (=l>98aojiblW) То-абсолютная темп-ра замерзания чистого растворите-тя, Qo--его скрытая теплота плавления в cal/a]. Свойства часто применяемых в криоскопии растворителей сопоставлены ниже в таблице. Зная депрессию At для данного раствора, легко вычислить относительное понижение давления пара: Др Qo At Ро Измеряя Д^, легко определить мол. в. М вещества в растворе; если в 1 ООО г растворителя растворено G г вещества, то с = и из (1) находим: Найденный так. обр. из нескольких определений At (при разных навесках G) мол. в. вещества часто не соответствует вычисленному из химич. ф-лы, т. к. вещество в растворе иногда находится либо в виде ассоциированных молекул (см. Ассоциация, Жидкости) либо диссоциировано на ионы, иногда сольвати-рованные (см. Ионы, Сольватация) или комплексные. Таким образом криоскопич. методом можно также пользоваться для определения молекулярного состояния вещества в растворе, степени его ассоциации или диссоциации. При этом = п (если w>l) называется коэфициентом ассоциа-Криоскопические свойства растворителе it. Вода, Н2О .... Бензол,СвНв (спец. очищишый, без тиофена) .... Нитробензол, CeHsNOa .... Уксусная кислота (ледяная), СНз СООН . Фенол, CeHjOH . Нафталин, CioHg Камфора, CioHieO 0=--I к11п. 5,5 б 17 41 80,1 180 79,67 30,4 22,6 46,4 29,1 35,6 5,12 7,5 3,9 7,3 6,9 40 80,3 Скрытая теплота кип., cal Молек. повыш. точки кипения, 0,516 2,65 Легко вычисляется и осмотическое давление (см.) разбавленного раствора Р: То 0 = То Р = 1 ООО .1т ц И и; если же w< 1, то г = - = - называется коэфициентом диссоциации; для электролитов, молекула которых образует V ионов, г=1 -f(v-1)а, где а-степень диссоциации. В пределе, при полной диссоциации а->1, i-*v; для бинарных электролитов г->2. Когда в растворе содержится не одно, а несколько растворенных веществ, концентрация которых в отдельности точно неизвестна, криоскопич. измерения применяются для определения суммарной (так наз. осмотической) концентрации раствора, вычисляемой по формуле с = ; сиобусловли- вает осмотич, давление раствора (P=RT с для слабых растворов). Так, К. применяется при физикохимическ. анализе сложных растворов, например мочи, минеральных вод. Измерение депрессии в концентрирован, растворах позволяет определить в них термодинамическую активность а растворенного вещества; если эту величину подставить вместо концентрации с во все термодинамические уравнения для слабых растворов, получим уравнения, справедливые и для растворов более концентрированных (исправленная концентрация). Для вычисления а концентрацию с умножают на коэфициент активности /, определи- 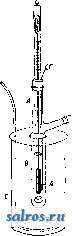 емый из величины депрессии; - = а = /-с; о f=, при а^с, /1. Методика измерений. Для нахождения At обычно применяют прибор Бек-мана (см. фиг.): во внутренний сосуд А, окруженный воздушной оболочкой В, на.яивают раствор или чистьп ! растворитель, а во внешний С помешают холодильную смесь (i° смеси д. б. на несколько градусов нилее темп-ры замерзания раствора). После переох-таждения основного раствора на 0,5-1° через боковую трубочку вносят при перемешивании затравку - кри-сталлик чистого растворителя, получаемый тут же в трубочке, погрулсенной в холодильн. смесь. Этим вызывается замерзание. Темн-ра замерзания измеряется обычно термометром Бекмана (см. Бекмана термо-Memjj). При этом измеряется до 0,001° (см. Термометрия). Для устранения ошибки от вымерзания части растворителя и повышения концентрации с во время опыта, в случае водных растворов, берут большие объемы растворителя (до 300 см), помешал их в смеси с мелкими кусочками льда в сосуд Дьюара. После установления по термометру Бекмана точки замерзания чистой воды в сосуд вливают из пипетки такой объем раствора, чтобы t° понизилась на 0,1- 0,2°. После нескольких отсчетов из раствора берут пробу для анализа, а затем прибавляют еше порцию раствора для второго ряда измерений. Камфора, по Расту, является удобным растворителем для криоскопических измерений (t j, 180°), так как дает большую молекулярную депрессию /го=40°=; поэтому в случае камфоры молено пользоваться обыкновенными термометрами, с делениями на 0,1-0,2°. Лит.: Вознесенский С. А. и Ребин-д е р П. А., Руководство к лабораторным работам по физической химии, М.-Л., 1928; А г п d t К., Phys.-chem. Messtechnik, 2 Aufl., Stg., 1923; R a s t, B , 1922, B. 55, p. 1051; Je 111 nek K., Lehrbuch d. phys. Chemie, B. 1-2, Stg., 1914-1915; Handbuch d. Arbeitsmethoden in d. anorgan. Chemie, hrsg. yon A. Stabler, B. 1-4, В.-Lpz., 1913-1925; H о u b e n J., Methoden der organischen Chemie, B. 1-4, Leipzig, 1923-1925. П. Ребиндер. КРИПТОСТЕГИЯ, каучук из мадагаскар-ской лианы Cryptosteffia grandiflora или С. madagascariensis (называется также 1отЫ-по ), среднего сорта, мягкий, при растягивании становится серо-белого цвета. Содержание млечного сока в растении незначительно, едва 2%. М. Лурье. КРИСТАДИН, кристаллический генератор и усилитель, основанный на явлении генерирования детектором незатухающих колебаний, подобно вольтовой дуге или электронной лампе, если обычный детекторный контакт G включить в колебательный контур LC (фиг. 1) и подвести к нему постоянный ток от батареи В через нек-рое балластное сопротивление i?. Период этих колебаний очень близок к собственному периоду кон-  Фиг. 1. тура. В качестве генерирующего контакта G м. б. применены негсоторые из обычных детекторных контактов (см. Детектор). Наилучшие результаты получаются с контактом минерала цинкита ZnO с примесями Мп и Fe (-Ь) и стальной проволочки (-); диаметр последней около 0,2 мм. Для улучшения действия криста.тлы цинкита предварительно обрабатываются в мощной электрич. печи []. Подобно дуговому преобразователю крис-тадинный генератор возбуждает обыкновенно колебания второго рода (см. Колебания электрические). С К. можно получать колебания всевозможных частот (в сторону понижения), в зависимости от значений L VL С присоединенного колебательного контура. Наиболее высокая частота, полученная с К., 1,23-10 пер/ск. (А=24,3 л*) []. Для целей приема удобна схема фиг. 2- двухдетекторная схема, в которой функции усиления и детектирования отделены: LC- обычный детекторный приемник с галеновым детектором й; батарея В 12 V; сила тока поддерживается S4mA. Схема фиг. 2 работает по принципу регенерации (см. Приемники). Релшм регенерации может быть регулируем: 1) посредством изменения силы тока-изменением напряжения при помощи потенциометра Р; 2) посредством изменения нагрузки - изменением детекторной связи приемника (на фиг. 2 не показано). Контур Ь'С низкой, слышимой частоты счужит для отыскивания генерирующих точек; c-o.z5fj.f ОН Д. б. отключаем во время приема. Действие генерирующего контакта объясняется: 1)чисто-теплевыми процессами в контакте , *, 2) чисто электронными процессами: диссоциация атомов кристаллич. решетки (см. Кристалл) активного места контакта. Несомненно таклсе, что при низких частотах имеется заметное влияние тепловых процессов [-, в, Минерал цинкит, обладая чисто электронной проводимостью, имеет отрицательный <°-ный коэфициент сопротивления, в пределах 22-97° равный -0,007 [\ Лит.: 1) Е с с 1 е S W. Н., The Electrician*, 1910. p. 385; Р i с к а г d С. W., Radio News , 1925, v. 6, p. 1166; ) Лосев О.. ТиТбП , 1922, 1, стр. 375; РЫ1. Mag. , L., 1928, р. 1024; О приложении уравнения теории квант к явлению свечения детектора, ТиТбП , 1929, оЗ; Радиолюбительство и радиовещание , Москва - Ленинград, 1926, стр. 181-187; ) Петровский А. А Морской сборник , СПБ, 1911. 10; ) Остроумов г. А., ТиТбП , 1924, 24, стр. 204; ) S 1 X t U S К., Zeitschrift f. techn. Phys. , Lpz., 1928. S, p. 70; ) К a p n о в с к и й А., ТиТбП , 1927, 43, стр. 449-451; S е i d 1 F., Phys. Ztsehr. , Lpz., 1926, B. 27, p. 64, 816. КРИСТАЛЛ, твердое химически однородное тело, обладающее анизотропией (см.) и б. ч. закономерной внешней формой. К. характе- 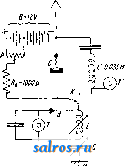 Фиг. 2. 1 ... 27 28 29 30 31 32 33 ... 49 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© 2007 SALROS.RU
ПромСтройМат |