• Что такое фактурная штукатурка
• Выбираем сухие строительные смеси
• Преимущества напряженного железобетона
• Что влияет на выбор кровельного материала
• В чем преимущество пробковых полов

чае будет: при положении груза равного 1 в правой части

1 2, = О, откуда D = +;

при положении груза =1 в левой части

-D8-1 I/ = О, откуда В =

где б-суммарное перемещение по направлению усилия D. Разница в знаках показы-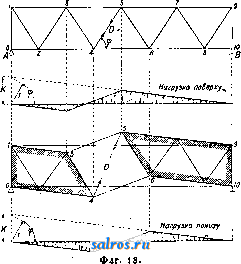

вает, что усилие раскоса имеет разные знаки в зависимости от положения нагрузки, как это и надо было ожидать (См. Ферми). Т. к. в данном случае точка моментов лежит в бесконечности, то относительное смещение обоих звеньев определяется отрезком к, величина же возможной деформации раскоса б = ft sin (р, что непосредственно видно по проекции полного перемещения к на направление раскоса.

В фермах со сложной решеткой, когда система превращается в механизм с целым рядом звеньев, целесообразно производить построение эпюры перемещений при помощи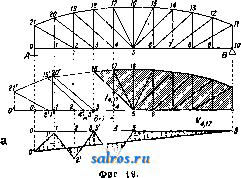

диаграммы или эпюры скоростей (см. Кине-матичесшй метод). В.а. фит. 19 показано построение диаграммы скоростей в двураскос-ной ферме при устранении из нее стержня стойки Vi,i а по ней эпюры возможных перемещений'для узлов нижнего пояса. При устранении стойки 4,17 узел 4 фермы получает возможность вертикального смеще-

ния с нек-рой скоростью 4-4, определяемой изображающей точкой 4 (см. Кинемог тический метод). По этой точке 4 строятся последовательно изображающие точки 3, 19, 20, 2, 1, 21 и О', определяющие скорости в узлах 3-3, 2-2, 1-1 и 0-0. Отложив эти отрезки в виде ординат от оси абсцисс, получим эпюру возможного смещения этих узлов относительно звена О-5, но т. к. опорный узел О не может иметь смещения, то эпюра д. б. исправлена поворотом всей фермы вокруг шарнира 10 так, чтобы в результате перемещение на опоре О было равно нулю; такой поворот всей системы характеризуется на эпюре вертикальных перемещений прямой 10-О'. Тогда величины действительных возможных перемещений всех узлов определятся разностью ординат этой прямой и ординат, полученных по диаграмме скоростей. Это непосредственно следует также из выражения возможной работы, к-рое изобразится так:

-Va,i7- Л-Луо-\-1-Ур==0,

Щ,1,-[-Луо + Ур],

но так как то

Переход от эпюры к Л. в. должен быть сделан из условия измерения ординат в^мас-штабе отрезка 4-4= 6=1.

Преимущество кинематическ. метода и в частности построения при помощи диаграммы скоростей заключается в том, что с помощью ее легко строить Л. в. для любого направления. Действительно все полученные по фиг. 19 отрезки скоростей были отложены нами по вертикальному направлению в полном виде, но они могли бьпъ отложены ио любому направлению в виде отрезков, равных проекции этих скоростей на новое направление.

Л. в. встатически неопределимых системах. Кинематическ. метод лежит также в основе построения Л. в. статически неопределимых систем; при построении Л. в. в этих системах устраняется лип-няя связь и изучаются перемещения грузовых точек системы, становящиеся возможными при устранении этой связи. При наличии в системе одной неизвестной X величина

ее определяется выражением Х=-р^ (см.

Статически неопределимые еит&иы), которое при действии на систему груза равного 1 приводится к виду

так как на основании теоремы о взаимности перемещений 6 = б .- В этом выражении числитель 6jj. представляет собой линейное перемещение по направлению груза равного 1, вызываемое единичным воздействием по направлению устраненной связи, а знаменатель представляет собой деформацию угловую или линейную по направлению самого неизвестного от того же единичного воздействия Х=1. Т. о. если будут известны

перемещения всех грузовых точек системы, вызываемые воздействием Х=1, т, е. будет найдена эпюра возможных перемещений, то при измерении ординат эпюры в Масштабе йаа.=1 получим Л. В. неизвестного. Построение эпюр перемещений целесообразнее делать графически при помощи упругих грузов, определяемых как угловые деформации: в сплошных системах из выражения

ds, а в сочлененных системах как угловые

деформации шарнирной цепи (см. Графиче-сш>е определен'ие перемещений). На фиг. 20 показано построение Л. в. в двупропетной балке с рассмотрением в ней, в качестве лишнего неизвестного, момента на средней опоре. Эпюра перемещений будет иметь вид двух кривых, показанных на чертеже; она представляет собой модель Л. в.; переход к Л. в. должен быть сделан путем установления масштаба 6д^=1.В данном случае деформация представляет собой угловую деформацию, определяемую тангенсом угла между касательными к обеим ветвям эпюры в точке приложения неизвестного момента. На фиг. 20 показано построение линии вли-17 яния в той же балке,

-*--2 но при условии рассмо-

f с трения в ней в каче-

1 стве лишнего неизвестного опорной реакции А. Эпюра перемещений, становящаяся возможной в системе при 1 устранении этой реак- ции, показана на том - же рисунке; она приводится к Л. в. этой реакции при измерении ее ординат в масштабе

ь

Фиг. 20.

Уо=1. На, фиг. 21 показано построение Л. в, для двухшарнирной арки, в которой за неизвестное принят распор Я. Эпюра перемещений, построенная по упругим грузам, определенным по угловым деформациям в шарнирной цепи, вызываемым воздействием £с(ЯХ=1, имеет вид кривой (фиг. 21, б). В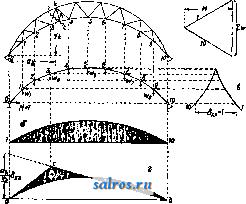

Фиг. 2i.

рассматриваемом случав определение масштабного множителя 5ая. = 1 д. б. сделано

или аналитич. расчетом по ф-ле 6=.

(см. Деформация) или графич. построецием эпюры перемепьений для горизонтального

направления, как это показано на той же фиг. 21, в. Построение Л. в. внутренних усилий статически .неопределимых систем после определения в ней Л. в. лишних неизвестных сводится к построению суммарных Л. в. по соответствующим ур-иям. Так напр., Л. в. поясного стержня той же арки, определяемая ур-ием вида

Щл-Улак-Ну, может быть построена как суммарная из ординат Л. в. реакции и ординат Л. в. распора Я, измененных помножением на постоянные множители. В целях упрощения перемножений ординат кривой Л. в. распора можно рекомендовать основывать построение на полученной кривой распора, вынеся множитель у^ за скобку; тогда

мз.4= f (f-Я). Отложив (фиг. 21. г) под левой опорой при построении Л. в. момента Vjaii вместо отрезка % отрезок щ в масштабе

Л. в. Я, т. е. б^., проводят прямую, определяющую правую прямую Л. в. момента 7%; левая прямая определится, как известно, точками а и с; общая суммарная Л. в. показанана той же фигуре штриховкой. Истинная величина ее ординат должна определиться помножением на два масштабных

множителя -т^ Этот прием удобоприме-

ним для всех статически неопределимых систем с одним неизвестным. При наличии в системе нескольких неизвестных вопрос с построением Л. в. осложняется, но в нем могут быть достигнуты упрощения специальными преобразованиями (см. Статически неопределимые системы). Для построения Л. в. в нек-рых общеупотребительных статически неопределимых системах существуют специальные таблицы: например для расчета неразрезных балок-таблицы Griot; для расчета сводов, заделанных пятами,-таблица Strassnera и др.

Л. в. деформаций.Потеоремеовза-имности перемещений всякое перемещение вида б„р=бр , из чего следует, что линейное перемещение <5,д, вызываемое единичным воздействием по направлению искомой деформации, по величине равно деформации бар, вызьшаемой действием груза равного 1, приложенного к грузовой точке системы, к которой относится перемещение бр. Отсюда следует, что линия прогибов, или эпюра перемещений, грузовой линии системы, возникающая от единичного воздействия, приложенного по направлению исследуемого пере-ремещения, является в то же время Л. в. этого перемещения. Построение эпюры перемещений м. б. сделано или аналитически по вычислениям ординат бра (см. Деформация) или графически при помощи упругих грузов (см. Графическое определение перемещений). Ординаты этих эпюр, измеренные в масштабе, соответствующем полюсному расстоянию равному 1, определяют собой Л. в. изучаемой деформации. В системах со сплош-, ными сечениями, где условия деформации в каждом сечении определяются выражением

вида W= ~ ds, построение эпюры перемещений, а следовательно Л. в., делается как ве-

ревочного мн-ка для фиктивного загружения системы эпюрой моментов при полюсном расстоянии равном 1 (фиг. 22). На фиг. 23 показано построение Л. в. деформации угла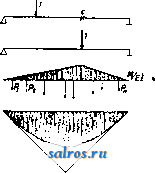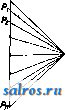

Фиг. 22.

а, образуемого раскосом и фермой. Приняв грузовую линию по верхним узлам фермы, вычисляют для нее фиктивные упругие грузы (угловые деформации в углах) от действия двух пар с моментами равными 1, приложенными к раскосу и элементу пояса для определения деформации угла. В рассматриваемом случае фиктивные грузы будут иметь место только в двух узлах:-TFи и-нРГц. Веревочный мн-к, построенный для них при полюсном расстоянии равном 1, имеет форму двух тр-ков и является Л. в. углового перемещения. Точное построение .Л. в. перемещений в фермах и в сочлененных системах связано с большими вычислениями величин упругих грузов. На практике Л. в. прогибов приходится пользоваться при испытании сооружений, в частности мостов, где.точность теоретическ. расчетов не соответствует точности измерительных приборов. В таких случаях вычисление ординат Л. в. прогибов можно делать по приближенным ф-лам инж. Качурина. Подсчеты показали, что расходимость вычислений по приближенным и точным ф-лам для простых решетчатых ферм с дополнителып>ши подвесками и- без них не

ТЬ 12 П Ю 9 в 7 S S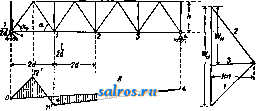

Фиг. 23.

превосходит 5%, тогда как расходимость между действительными и'теоретическими прогибами доходит до 10%.

Обобщенные Л. в.Подэтимназвали-ем известны Л. в.,характеризуюпще собой не влияние груза равного 1, как это имеет место в обычных Л. в., а целой системы грузов, имеющих разлотную величину и отстоящих друг от друга на определенных и неизменяемых расстояниях. Применение обобщенных Л. в. имеет большое значение для испытания мостов. Инж. И. М. Рабинович

предложил строить эти обобщенные линии влинния как веревочный многоугольник от специальной системы грузов. Например если требуется построить обобщенную Л. в. для среднего сечения балки от поезда по схеме, показанной на фиг. 24, то балку надо рассматривать под дей- ствием трех поездов, in обозначенных на том же чертеже цифрами

Иапрввл&ше движений

Фиг. 2

I, II и III. Все эти поезда получаются поворотом действительного поезда на 180°. Поезд 1 ставится своей передней осью над исследуемым сечением; грузы его положительны. Остальные два поезда-реактивные поезда-ставятся своими передними осями над опорами, все грузы их равны половине веса действительных и направлены в обратную сторону. Вся система грузов уравновешена и веревочный многоугольник ее будет замкнутый. Этот веревочный мн-к и представляет собой обобщенную Л. в. момента в рассматриваемом сечении. Прием этот м. б. использован для построения любой обобщенной Л. в., соответственно изменяются только число положительных и отрицательных поездов и коэфициенты их пропорциональности по отношению к действительному поезду. На фиг. 25

Масштаб ординат: 1а1=40к?/см*

Фиг. 26.

Фиг. 25.

показана построенная указанным способом обобщенная Л. в. усилия в раскосе балочной фермы пролетом 27,0 л* от паровоза серии Щ. Каждая ордината диаграммы соответствует тому положению паровоза, когда передняя ось его стоит над этой ординатой. ОеобьаЙ интерес обобщенных Л. в. заключается в том, что они могут быть построены'для динамического действия нагрузки (фиг. 26). Несомненно, что этот вид Л, в. должен получить большое развитие в деле испытания мостов.

Лит.: М ю л л е р-В р е с л а у Г., Графич. статика сооружений, т. 2, ч. 1, пер. с немецкого, 2 изд., СПБ, 1910; Патон Е. Ф. и Горбунов Б. Н.. Стальные мосты, т. 1, Киев, 1929; П а т о н Е. Ф., Таблицы для проектирования деревянных и стальных мостов, Каев, 1929; Прокофьев, Теория сооружения, ч. 1-2, М.. 1926-28; Тимошенко С. П., Курс статики сооружений, ч. 1, Л., 1926; Качурин В., Линии влияния для прогибов и перемещений сквозных ферм, Труды научно-технического к-та НКПС , М., 1927, вып. 60; Рабинович И., Кинематич. метод в строит, механике, М., 1928; его же, Нек-рые способы исследования диаграмм, получаемых при испытании мостов, Труды бюро мостов исслед. научно-техн.к-та НКПС , М., 1923,сб. 3; Грио Г.,Интерполяционные таблицы для быстрого построения инфлюен-тных линий моментов и поперечных сил, а также для равномерно распределенных нагрузок и сосредоточенного груза, пер. с нем., М., 1928; DoorentzR., Abreitungd.EinflussIinien, Strassburg, 1921;L a n d s-berg Tb, Das Verfahren d. Einflusslinien, 7 Aufl., в., 1920; Marcu s H., Die Einflusslinien mehrfach gestutzter RahmentrS.ger, В., 1915. И. Прокофье*.

ЛИНИИ ПЕРЕДАЧИ,устройство для транспорта э л ектрич. энергии из места производства в места потребления энергии. Л. п. мо-

гут быть воздушными или подземными, в последнем' случае передача энергии производится по подземным кабелям (см. Кабель высоковольтный), причем обычно передача электрич. энергии по подземным кабелям производится только на сравнительно небольшие расстояния. При более значительных расстояниях, порядка 100 ш и более, передача электрич. энергии производится всегда по воздушным Л. п. Последние состоят из голых проводов, поддерживаемых линейными изоляторами (см, Изо-лятдры электрические); последние укрепляются через известные промежутки на специальных мачтах-опорах, соединяющих между собой место генерации электрической энергии (генераторный конец Л. п.) с местом потребления энергии (приемный конец Л. п.). В настоящее время имеются уже осуществленные проекты Л. п., некоторым передается до 150 ООО kW по одной линии на расстоянии до нескольких сотен км. При передаче столь больших мощностей на такие большие расстояния, во избежание чрезмерных потерь в Л. п. или чрезмерных сечений проводов, необходимо вести передачу при весьма больших напряжениях, достигающих в настоящее время в уже работающих установках до 220 kV. В связи с большой протяженностью Л. п. и значительной величиной применяемых напряжений емкость линии начинает играть заметную роль в процессе передачи энергци, и картина явлений, происходящих в длинных Л. п., сильно отличается от явлений в коротких линиях.

Электрический расчет Л. п. Омич. сопротивление R провода Л. п. равно:

где I--длина провода в км, q-сечение провода в лш , Q-удельное сопротивление материала провода в Q MMJKM.

Значения удельных сопротивлений'раз-личных материалов приведены в табл. 1.

1.-*Значения с для материалов.

р азличных

При переменном токе сопротивление будет несколько больше, вследствие влияния скин-эффекта (см.). В этом случае сопротивление провода будет

Pnep.- noem.t (2)

где к-коэф. скин-эффекта. Для сплошных цилиндрич. проводов и тросов коэф. СКИНг эффекта равен

£:=1-Ь2,оз/-!*-з,з^-Ч...; (з;

d-диам. провода в см. Так как магнитная проницаемость ц ферромагнитных материалов зависит от индукции, то сопротивление биметаллич. проводов зависит от силы тока в них. Зависимость омич. сопротивления биметаллич. проводов (алюмйний-сталь) иллюстрируется данными табл. 2.

Табл. 2.-Омическое сопротивление биметаллических проводников.

Рабочая самоиндукция провода линии при применении транспозиции проводов равна

L = (0,461g + 0,05 -Ь 0,2 . 10-3Н/кл*, (4)

где г-радиус провода в см, D-расстояние между центрами проводов в см. При трехфазной линии с транспозицией проводов под D следует понимать среднее геометрич. рас-стояниб между проводами

где Di8,X>i8, JDga-соответственно расстояния между проводами 1-2, 1-3 и 2-3. Так как для воздушных линий г мало по, сравнению .0*1), то в этом случае ф-ла (4) примет вид:

L = (0,46 -}- 0,0б) -10-8 Н/км. (4а)

Индуктивное сопротивление линии

x=27tfl.lQ. (6)

Кажущееся сопротивление провода линии

Z = V+U Q. (7)

Рабочая емкость линии без учета влияния земли

0,0241 10-

¥jKM.

Рабочая емкость с учетом

0,0241 10-е

ВЛИЯНИЯ земли

¥JKM,

где Ь-среднее геометрическое высот проводов над землей и а-среднее геометрическое расстояний от проводов до их зеркальных изображений.

2\Г^- (10)

Реактивная проводимость провода линии В=2я/С1мо. (11)

Активная проводимость провода линии передачи fir складывается из потерь в изоляторах и потерь на корону.

Потери в изоляторах изменяются прямо пропорционально частоте, вьппе при деревянных штырях, чем при железных, выше при тумане или мелком дожде, чем в хорошую погоду или при сильном дожде или при обледенелых изоляторах. Результаты измерений потерь в штыревом изоляторе на рабочее напряжение ок. 60 kV даны в табл. 3.

Табл. 3.-П от ер и в штыревом изоляторе.

Омическое сопротивление одного элемента гирлянды подвесных изоляторов в сухом виде равно CXD, а при смоченной дождем верхней поверхности равно ~80 MQ. Потери на корону в проводе Л. п. равны

р = 4* (/+25)1 .10- Ш/км; (12)

Е-рабочее напряжение линии в kV, Eg- критич. коронное напряжение;

S = 48,9m 5rlg5 kV, (13)

где m-коэф., учитывающий состояние поверхности; для полированных проводов т = = 1; для сплошных неполированных проводов т= 0,93-0,98; для витых проводов т = 0,824-0,86; 8-плотность воздуха:

б=?\ (14)

-барометрическое давление в см ртугно-столба). Зависимость д от высоты над уровнем моря дана на кривой фиг. 1. Во время снежной бури потери на корону сильно увеличиваются и м. б. вычислены (Eff принимают равным 80% его значения при хорошей погоде). Во избежание боль- im 2000 зттом ших потерь на корону в

Высота над уровнем моря уСЛОВИЯХ бурИ НбОбхО-

димо стремиться к тому,

чтобы JE?o, вычисленное по ф-ле (13), было больше В рабочего напря= жения линии.

Характеристиками Л. п. называются кривые зависимости ряда величин от мощности Ра на приемном конце линии. Эти величины суть: Р^-мощность на генераторном конце Л. п.; и 1-силы тока на генераторном и приемном концах Л. п.; Е^и Ei-напряжения на генераторном и прйемно^! концах Л. п.; cos 97, и cos -коэф-ты мопщо-сти на концах Л. п.; г]-кпд Л. п.; 1, и РГ,- ток и мопщость синхронных компенсаторов. Ур-йя Л. п, имеют вид:

E,=E.,cbVJ + Y Wo f) Ji=l2ch/ + KS,8hv/o, (16)

где и

o=(R-f ?х) Q

Уо=(9-1В) MO.

Обычно при отсутствии потерь на корону можно принимать д = 0. По мере удаления от приемного конца Л. п., как это следует из ур-ий, (15) и (16), действующие значения си-

лы тока и напряжения будут в общем возрастать, причем возрастание будет итти не беспрерывно, а волнообразно, с длиной волны

т. о. в отдельных случаях при длинных Л. п. сила тока и напряжение на генераторном конце м. б вследствие влияния распределенной емкости Л. п. менее силы тока и напряжения на приемном конце. Фазный сдвиг между током и напряжением также меняется вдоль Л. п. и м. б. то отстающим, то опережающим. Так как сила тока, напряжение и фазный угол беспрерывно изменяются вдоль линии, то очевидно,что,вообще говоря,потери в линии будут больше джоулевых потерь, рассчитанных по силе тока приемного конца, и падение напряжения в Л. п. будет больше омич. падения напряжения. В тех случаях, когда электрич. и магнитная энергии в Л. п. полностью компенсируют друг друга, потери в Л. п. будут равны омическим потерям. Это условие удовлетворяется при нагрузке Р, значение которой дается следующим выражением:

где Е^-фазное напряжение на приемном конце Л. пг в V. Если длина линии передачи

Т. е. равна четверти длины волны, то условия компенсации электрической и магнитной энергии удовлетворяются при всех нагрузках. Ур-ия (15) и (16) имеют сложный вид и неудобны для расчетов, почему ими рекомендуется пользоваться только при расчете очень длинных Л. п. Для линий длтаой до 500 км можно с достаточной точностью заменить ур-ия (15) и (16) следующими ур-иями:

EtE,(l + )+zll,(l-f)=A + jB, (17)

Ii-h(l + -f)+yoE,(l + -f)-C+jD (18) или в более удобной для расчета форме: Ei=a{E-\- lojn cos (a-q>z)} -f-+ ja {E,Pt +1 sin (<T- q>,)]=A + jB, (19) Ix=yl2COs((p2-r)-E.ia + -h? {BjBa-yJa sin (9?2-t)\ = G + jD. (20)

В уравнениях (19) и (20) все величины (кроме El и Ii) представляют собою абсолютные значения, т. е. o= УИ + х^ и т. п.

При частоте f = 50 можно с достаточной точностью принять:

а = 1-0,193512-Ю-*, (21а)

=1-0,387 12-10-*, (22а)

у=1-0,581 12.10-*. (23а)

Л. п. оканчивается у трансформаторов, в которых сопротивление, самоиндукция и емкость уже не распределенные, как в линии а сосредоточенные. При необходимости определения напряжений и т. д. на стороне низкого напряжения необходимо учитывать влияние трансформаторов. Расчет можно произвести двумя ступенями, рассматривая сначала явление в линии и накладывая затем на них падение напряжения и т. д. в трансформаторах. Иногда удобно принимать постоянные трансформаторов не сосредоточенными, а распределенными и прибашлять их непосредственно к постоянным линии, чрго сводит расчет к одной операции без большого ущерба в точности, в особенности при коротких линиях-. Намагничивающий ток нормальных силовых трансформаторов изменяется в пределах 3-6% от тока полной нагрузки, потери в жзлезе 72-1% и потери в меди -174% от номинальной мощности трансформатора. Омическое падение напряжения IR составляет обычно - 1 % от номинального напряжения трансформатора. Реактивное падение напряжения /ж в % за-висиг от напряжения (см. Короткое замыкание). По вьппеприведенным данньм могут быть легко вычислены необходимые для расчета постоянные трансформаторов.

Для сравнительно коротких линий, не длиннее 65-80 км, и напряжений, не превосходящих 50-60 kV, влиянием емкости и утечки можно пренебречь, причем уравнения Л. п. примут вид:

E, = E, + Zoh, (27)

J, = J,. (28)

Нормально при передаче электрич. энергии по Л. п. напряжение у приемного конца должно поддерживаться постоянным при всех нагрузках. Это м. б. достигнуто например путем изменения напряжения генератора. Относительное изменение напряжения генератора в % от постоянного напряжения приемника при изменении нагрузки от холостого хода до полной называется регулированием линии:

ДВ = --100%. (29)

Величина АЕ зависит гл. обр. от реактивности линии. В целях удобства эксплоатации регулирование линии не должно превосходить 10-15% и максимум в исключительных случаях 22%. Регулирование линии м. б. вьгаислено по вышеприведенным-ур-иям Л. п.(15), (19) или (27), в зависимости от длины линии. С достаточной точностью регулирование линий может быть вычислено по следующей ф-ле:

Д£7= а

mzo cos (а-(р^) + т^ 100 %, (30)

2 J

где

. (31)

(/а-ТОК на приемном конце при полной на-

грузке). Т. к. при постоянном напряжении на приемном конце Л. п. напряжение на генераторном конце зависит от коэф-та мощности, то, если регулирование линии получается более допустимьк пределов, возможно поддерживать постоянные напряжения на обоих концах Л. п. путем искусственного изменения коэф-та мощности. Такое изменение коэфициента мощности м. б. выполнено при помощи синхронных компенсаторов, т. е. синхронных двигателей, дающих, как известно, при недовозбуждении отстающий, а при перевозбуждении опережающий ток. Двайт (Н. В. Dwight) показал, что для поддержания постоянства напряжения на приемном конце линии при постоянном напря--жении^на генераторном конце необходимо, чтобы конец вектора тока J а скользил по кругу, координаты центра к-рого и радиус зависят от постоянных линии и напряжения. Координаты центра круга синхронных компенсаторов и радиус кругам.б.с достаточной точностью вычислены по следующим ф-лам:

-cos(9.4.f-To), -*sin (<p + i-T ),

где

(32) (33) (34)

(35) (36)

Для линий не длиннее 200-300 км можно с достаточной точностью пользоваться вместо ф-л (32) и (33) ф-лами

(37) (38)

Окружность круга синхронным компенсаторов Эллипс тока

Ток синхронных компенсаторов, а следовательно и их реактивная мощность, могут быть определены путем построения диаграммы (фиг. 2). При холостом ходе синхронные компенсаторы посылают в линию отстающий ток, который с увеличением нагрузки постепенно уменьшается, доходит до нуля и при полной нагрузке становится опережающим. При увеличении напряжения J?iOTCTa-ющий ток синхронных компенсаторов увеличивается, а опере^ жающий уменьшается.

Наивипгоднейшим является такое напряжение генераторного конца Е^, при котором максимальный опережающий и отстающий токи равны, т. к. очевидно, что мощность синхронных компенсаторов при этом получается минимальной. Однако в виду неустойчивости работы сильно недовозбужденных синхронных двигателей на практике обычно выбирается Е^ т. обр., чтобы максимум отстающего тока равнялся 60-75% максимума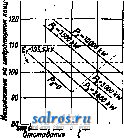

шшвооо >пережвиив

Фиг. 3.

опережающего тока (тока синхронных компенсаторов при полной нагрузке). Выбор напряжения Ei м. б. сделан на диаграмме фиг. 2 путем подбора величины г, удовлетворяющей вышеуказанным условиям. Тогда напряжение Е^ находится по ф-ле (34).

Другой способ определения мощности синхронных компенсаторов заключается в следующем. Строятся кривые зависимости генераторного .напряжения от коэф-та мощности приемника при различных нагрузках. Для данной постоянной величины Е^ и cos 9?а коэф-т мощности на приемном конце зависит от мощности синхронных компенсаторов,

jy -которая для удобства

J50\ Г I I I и откладьшается на оси абсцисс. Построенные т. о. зависимости (фиг. 3) практически представляют собою прямые линии, за исключением очень больших перегрузок и малых коэф-тов мощности cos 9?g. В виду этого для построения зависимости достаточно для каждой нагрузки вычислить две точки, соответствующие следующим условиям: 1) мощность синхронных компенсаторов Wg= О и 2) коэф-т мощности приемного конца равен 1. Пересечение зеркального изображения кривой для холостого хода относительно оси Wg= О с кривой полной нагрузки дает точку, определяющую мощность синхронных компенсаторов и напряжение генераторного конца при условии равенства отстающей и опережающей мощностей компенсаторов. При неравенстве отстающей и опережающей мощностей необходимо только соответственно изменить ось, относительно которой строится зеркальное изображение кривой холостого хода. Пересечения кривых для других нагрузок с прямой линией, соответствующей полученному указанным способом напряжению Е^, дают точки, определяющие мощность синхронных компенсаторов при этих нагрузках. Суммируя найденное значение тока синхронного компенсатора с током нагрузки (геометрически), получаем полный ток на приемном конце Л. п. Зная полный ток приемного конца, характеристики Л. п. можно вьгаислить по приведенным вьппе ур-иям, напр. (19) и (20). Потери в синхронных компенсаторах равны 3-4% от их реактивной мощности.

Перенапряжения в Л. п. и выбор изоляции. Перенапряжения в Л. п. могут быть разбиты на следующие группы: 1) перенапряжения внутреннего характера вследствие процессов включения и вьпслючения; 2) перенапряжения вследствие заземляюпщх дуг; 3) перенапряжения атмосферного характера. Перенапряжения при включении и выключении разомкнутой линии обычно не превосходят 70-100% от номинального напряжения Л. п. В отдельных случаях были зарегистрированы перенапряжения, в 6 раз превышающие номинальное фазное напряжение Л. п. Наиболее неблаго-

приятные условия получаются при оперативности на стороне высокого напряжения. Выключение и включение нагрузки вызывают обьгано очень небольшие перенапряжения. При выключении коротко-замкнутой линии

запасенная магнитная энергия --перехо-дит в электростатическую энергию т. е.

т.о. возникающие при этом перенапряжения будут тем больше, чем меньше емкость С и чем больше ток короткого замьпсания J.

Вьшлючение короткого замьжания наиболее опасно при оперативности на стороне низкого напряжения. Судя по произведенным наблюдениям на работающих америк. линиях, перенапряжения при вьшлючении коротких замьжаний не превосходят 5 - 6-кратной величины от нормального фазного напряжения Л. п. Такие перенапряжения для современной изоляции Л. п. и аппаратов нормально не представляют опасности. Перенапряжения вследствие заземляющих дуг, возникающие при генерировании дугой вы-сокочастотньЕЕ колебаний, наиболее опасны на системах с изолированной нейтралью. Ниже приведены теоретические максимальные напряжения, могущие быть полученными при различных условиях и вычисленные Клемом (I. Е. Clem).

Кратность перенапря-

УСЛОВИЯ расчета

нию л. п.

Без учета затухания...... 7,5

С учетом затухания...... 6,7

С учетом затухания и емкости

между проводами........ 5,5

При заземлении нейтрати через сопротивление не больше критического ............ 2,5

При наглухо заземленной нейтрали.............. 1,0

Критич. сопротивление в нейтрали, при котором перенапряжение вследствие заземляющих дуг не превосходит 2,5-кратной величины от фазного напряжения Л. п., может быть вычислено по следующей ф-ле, выведенной Кларком (Е. Clark):

- П./ШМ, (39)

где Е-линейное напряжение в kV; х-реактивность системы до места аварии в % от мощности Р^; Jg-зарядный ток в заземляющей дуге; к-отношение отстающей составляющей-тока короткого замыкания к 1. Для быстрого гашения дуги проф. Петерсеном было предложено заземлять нейтраль трансформаторов через реактивную катушку, подобранную т. обр., чтобы скомпенсировать емкостный ток в заземляющей дуге. Тем не менее в условиях дождя, при наличии заметной активной составляющей тока заземления, катушка Петерсена не может вызвать гашения дуги и даже, наоборот, может сама явиться источником значительных перенапряжений. Наилучшим способом борьбы с заземляющими дугами является все же заземление нейтрали или наглухо или через со-

противление, не превосходящее-критической величины (ф-ла Кларка).

Наиболее опасными для изоляции Л. п. и оконечных подстанций являются перенапряжения атмосферного характера. Атмосферные перенапряжения носят всегда характер импульсов или быстро затухающих колебаний очень высокой частоты.

Возникновение перенапряжений атмосферного характера м. б. представлено след. обр. Когда над проводом Л. п. находится заряженное грозовое облако, то на проводе индухстируется связанный аряд противоположного знака, плотность в которого в точке X будет

где С-емкость провода на единицу ;ины, fc-высота провода над землей, д-градиент земного потенциала. При мгновенном разряде заряда облака заряд на проводе Л. п. освобождается, причем потенциал провода будет

Так как в действительности облако не может разрядиться мгновенно и разряд длится конечный промежуток времени, то действительная амплитуда перенапряжения, возникающего на проводе Л., п. при разряде грозового облака, будет

V=agh, (40)

где коэф. \ TS. зависит от скорости и закона разряда облака и распределения связанного заряда вдоль провода Л. п. После освобождения заряда последний начинает двигаться в две противоположные стороны, образуя две блуждающих волны, амплитуда напряжения к-рых будет

Fi = of/h, (40а)

причем коэф. а'0,5. В табл. 4 приведены значения коэф-тов а и а' в предположении равномерного распределения связанного заряда вдоль Провода Л. п.

Табл. 4.-3 н а ч о н и я а и а'.

Градиент потенциала земли может при сильных грозах достигать значений до 330 кУ/л .

(Для уменьшения амплитуды атмосферных перенапряжений применяется защита линий при помощи заземленных тросов, протянутых над проводами Л. п. Отношение амплитуды перенапряжения при защите Л. п. заземляющими тросами к амплитуде перенапряжения без тросов называется к о э ф и ц и-ентомзащиты. Значения коэфициента защиты при различных расположениях проводов и тросов даны в табл. 5. Из рассмотрения табл. 5 очевидно преимущество горизонтального расположения проводов,так как

в этрм случае мы кроме понижения высоты подвеса провода улучшаем также и защитное действие троса. При двух заземленных тросах и горизонтальном расположении проводов коэф. защиты м. б. принят равным О, 37. Табл. 5.-К о э ф и ц и е н т ы защиты.

Выбор изоляции л. п. делается обычно по существующим нормам, т. е. выбирается такой изолятор или число элементов гирлянды изоляторов, разрядное напряжение которого удовлетворяет условиям норм.Однакотаккак нормируется разрядное напряжение при промышленной частоте, а наиболее опасные перенапряжения носят всегда характер импульсов, то выбор изоляции по нормам не всегда обеспечивает бесперебойную работу линии передачи. Для полного обеспечения линии от перекрытия изоляторов изоляцию линии выбирают, исходя из импульсного разрядного напряжения и высоты подвески провода над землей.

Зависимость величины разрядного напряжения от числа элементов в гирлянде шарнирных изоляторов {0 элемента-254 мм и расстояние между элементами-146 мм) при импульсе и при промышленной частоте дана в графической форме на фиг. 4. При расчете амплитуды атмосферных перенапряжений градиент земного потенциала в большинстве случаев достаточно принимать равным 250 kV/j№ и только в местностях с усиленной грозовой деятельностью увеличивать эту цифру до 330 kV/л*.

Очень сильная изоляция Л. п. может создать благоприятные условия для попадания волн с большой амплитудой на подстанцию. Во

избежание этого ближайшие к подстанции участки Л. п. следует делать с ослабленной изоляцией и с усиленной защитой тросами. Длину ослабленного участка выбирают исходя из того, чтобы волна перенапряжения,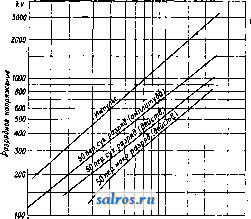

2 4 6 10

Яиш изоляторов в гирлянде

Фиг. 4.

20 30 40

возникшая за пределами этого участка, успела достаточно затухнуть до попадания на подстанцию. Затухание волны вдоль линии м. б. вычислено по ф-ле (эмпирической):

где во-начальн. амплитуда волны в kV; i- расстояние до места возникновения волны в кл*. Максимальное возможное значение для любой линии будет импульсное разрядное напряжение изоляторов. При выборе подвесных изоляторов необходимо иметь в виду, что распределение потенциала вдоль гирлянды происходит неравномерно вслед--ствие ВЛИЯШ1Я емкостей арматуры изолятора относитед1Ьно земли и провода Л. п.

Выбор расстояния между проводами. Выбор расстояния между проводами Л. п. должен быть произведен т. о., чтобы при максимальном возможном сближении проводов разрядное напряжение между ними при плотности воздуха 6=0,9 (условия бури) бьшо не менее полуторного рабочего напряжения Л. п. Разрядное напря-жение по отношению к нейтрали м. б. вычи--слено по ф-ле Пика:

Ешв^дтаПт^ Удейств., (42)

причем при больших расстояниях у > 30 д^, = 21,2 <5 m (l +~ kV/em, (43)

при <30

д^,21,2дт (l + ) кУ/сл*. (44)

Сближение проводов может произойти или вследствие их раскачивания ветром, или ©следствие неодинаковой нагрузки вертикально расположенных проводов, или всл'ед-чгтвие раскачивания проводов электродина-мич. взаимодействием токов короткого замыкания. При горизонтальном расположении максимальн. сближение проводов будет при

т. 9. т. XII.

ИХ асинхронном раскачивании. При расчете качания проводов под действием ветра достаточно принимать расхождение фаз качания на 90°. При вертикальном расположении проводов наиболее оПасным является сброс гололеда на одном пролете нижнего провода. Анализ вопроса показывает, что в этом случае сближение проводов практически не зависит от пролета Л. п.

При приблизительных расчетах можно определить расстояние между проводами при горизонтальном расположении их по формуле, предложенной инж. А. А. Глазуновым:

D=(A--hBE)cM, (45)

где i-длина пролета в м, е-линейное напряжение в началелинии вкУ.При jE7<40kV:

4 = 1,4, Б = 1; при .Е7>40 kV:

4=0,75. В = 2,2. Вертикальное расстояние между проводами Л. п. может быть определено по формуле инж. А. М. Залесского:

= (120 4- 0,155 S ) см. (46) Расстояние между проводами и частями опор м. б. определено по ф-лепроф. А, А. Смурова:

d = (15,7 4- 5,75 Уе) см, (47)

причем в случае подвесных изоляторов принимается отклонение гирлянд на 45 .

Ф-лы (45), (46) и (47) не учитывают отАло-нения проводов электродинамич. силами при коротком замьшании. В этом случае максимальное горизонтальное отклонение провода м. б. вычислено из ур-ия:

0,29/оу 1п^±=2 890-2-0,092, (48)

где -максимальное горизонтальное отклонение провода в см, fa-начальная стрела провеса провода в см, а-начальное Напряжение в материале провода в кг/см, к- отношение веса провода с гололедом к весу голого провода, t-время в ск., необходимое для достижения максимального отклонения. На основании произведенных Петерсоном и Мак Крекеном опытов можно принимать в среднем t = 0,3-1,2 ск. Ур-ие (48) легче всего решать путем подбора.

Устойчивость работы Л. п. Каждая данная Л. п. имеет нек-рую предельную мощность, которую можно передать по Л. п. При переходе через этот предел устойчивость работы нарушается и происходит выпадение из синхронизма. Устойчивость работы тем меньше, чем больше кажущееся сопротивление между генератором и мотором. На больших высоковольтных Л. п. зарядный ток понижает необходимое возбуждение машины и может таким образол! привести к уменьшению устойчивости работы. Поэтому максимальная мощность, которая может быть передана по Л. п. при увеличении числа цепей, сначала увеличивается, а потом снова падает (фиг. 5).

2 3 4 5-6 7 8 3 Ю11 Число линии

Фиг. 5.

Необходимо различать устойчивость работы Л. п. при установившемся и при устанавливающемся режиме работы. Устойчивость работы при установившемся режиме работы сильно эависит от системы регулирования напряжения и от типа возбудителя. При замене Л. п. по Кенелли эквивалентной п линией максимальная мощность, которая м. б. передана по Л. п. при установившемся режиме работы, м. б. вычислена по ф-ле, предложенной Никле (С. А. Nickle):

(f)V(.l.f)(4-)

(49)

где E-линеДное напряжение передачи, х\- эквивалентная реактивность генератора, х'- эквивалентная реактивность мотора, х-эквивалентная реактивность линии. В виду наличия многих влияющих и неучитываемых факторов точный расчет максимальной мощ- ности возможно произвести лишь в простейших случаях. Расчет устойчивости работы Л. п. при устанавливающемся режиме работы представляет собою чрезвычайно сложную задачу и обычно не может быть произведен. Испытания работающих систем показали, что предел устойчивости работы Л. п. при устанавливающемся режиме работы со-,ставляет от 30 до 60% от Р^ах при установившемся режиме.

Механический расчет Л. п. Расчет проводов имеет целью определить тяжения и провесы проводов при различных условиях для решения задач по выбору расположения проводов, трасировке линий, монтажу и т. п. Провес проводов определяется по ф-ле:

/=Й->> (50)

где д-нагрузка провода в %г]м, I-пролет в ж, о-напряжение в материале провода в кг/л^лг, q-сечение провода в мм. Если обозначить

р = ~ кг/м-мм, (51)

то по заданньш начальньв! условиям (cr , рд и о) напряжение в материале провода при любых условиях может быть определено из уравнения:

1 ртЕ £ Р?)Е а2 24 1 ~

-aE(t-io)~, (52)

где Е-модуль упругости материала проводов, а-температурный коэф. линейного расширения материала проводов, t-темц-ра в °С, д-изменение пролета, причем знак - соответствует уменьшению пролета, а + увеличению. Механические свойства многопроволочных проводов по нормам ЦЭС приведены в табл. 6.

Максимальное напряжение в материале провода при пролете больше критического имеет место при t =5° и нагрузке гололедом и ветром, а при пролетах меньше критического при t = tin- Критич. пролет Определяется по следующей формуле:

hp. = TVHtin-t,) м. (53)

.Знак О соответствует условиям гололеда. Максимальный провес проводов может иметь

Т а б л. 6.-М е x а н и ч е с к и е свойства многопроволочных проводов.

место ИЛИ при 1 = 1{есля Ь^хУкр) или при нагрузке гололедом и < = -5° {tmax<iKp)-Критич. t° м. б. рассчитана по ф-ле;

(54>

По нормам ЦЭС следует принимать толщину гололеда 1 см при уД. весе льда=0,9 и.давле-ние ветра на провода р^ = 24 кг/м^, относя давление ветра к проекциям провода. При раскачивании проводов ветром максимальный угол качания имеет место при i = - 5° и нагрузке гололедом толщиной

8 = У00036 fq-0,2b - 0,5 d, (55) где d-диам. провода в см. Если по ф-ле (55) й > 1 cjvt, то в расчет следует вводить б = 1 сж.

Нагрузки, действующие-на опоры Л. п., определяются по нормам ЦЭС в соответствии с вьппеизложенным. Наиболее тяжелым случаем является односторонний обрыв части проводов (обрыв двух проводов из трех). При определении приложенных в этом случае к опоре сил тяжений проводов при расчете про-межуточньЕх; опор с подвесными изоляторами необходимо считаться с уменьшением тя жения проводов вследствие отклонения гирлянд. Уменьшение тяжения проводов в этом случае будет тем незначительнее, чем больше пролетов имеется между анкерными опорами^ Т.к. опоры имеют нормально некоторую гиб^ кость, то необходимо учитывать также и отклонение вершины опоры, также уменьшаю-ш;ее натяжение проводов. Расчет уменьшения натяжений вследствие отклойения гирлянд и верхушек опор производят проще всего путем подбора, задаваясь условиями на анкерной опоре и проверяя по ним условия на последней опоре у оборванного пролета. При наличии заземленного троса необходимо считаться с тем, что часть нагрузок берет на себя трос. После определения действующих на опору нагрузок расчет опор производится нормальными методами строительной механики..

Экономический расчет Л. п. Задача снабжения электрич. энергией промышленных центров может быть разрешена или постройкой электрич. станции на месте нагрузки и транспортом топлива для питания такой станции или же непосредственным транспортом электрич. энергии через Л. п. При экономич. обосновании целесообразности постройки Л. п. могут встретиться два основных случая. При передаче энергии от тепловой электрич.станции необходимо сравнить стоимость транспорта электрич; энергии по Л. п. со стоимостью транспорта топлива. При передаче электрич. энергии с гидроэлектрич. станции необходимо сравнивать стоимость энергии от