• Что такое фактурная штукатурка
• Выбираем сухие строительные смеси
• Преимущества напряженного железобетона
• Что влияет на выбор кровельного материала
• В чем преимущество пробковых полов

Фиг. 3.

приводгошй в колебательное движение кривошипом и шатуном; Л. этого типа пригодны лишь для работ, не требующих высокой степени точности; 3) Л. с движущейся поступательно рамкой (фиг. 3); этот тип станков получил в последи, время значительное распространение в металлообрабатывающей промышленности для выработки сквозных отверстий в штампах и матрицах, причем время обработки сокращается на 6 О-75 % сравнительно с употреблявшимся прежде методом высверливания ряда отверстий и последующей опиловки вручную. Станок состоит из рамки А, движущейся по двум цилиндрическим направляющим и приводимой в движение кривошип-но-шатунньш механизмом, скрытьш в цоколе машины. Нажатие (jбpaбaтывaeмoгo предмета на пилку производится при помощи особого груза Б, натягивающего две цепи В, прикрепленные к рамке, в к-рую зажимают обрабатьшаемый предмет; благодаря этому нажатие производится всегда с одинаковой оптимальной силой и на долю рабочего приходится лишь направление обрабатьгеаемого предмета.

Пилки для ручных Л. имеют длину от 125 до 130 лш, для машинных-от 130 доЗООлш II изготовляются различной нумерации, по величине зубцов. Пилки для обработки дерева и металла делают из стали различногр качества, причем с чисто внешней стороны они различаются тем, что пилки для дерева отпущены до соломенно-желтого цвета, а для металла-до синего. До войны 1914- 1918 гг. все производство пилок для Л. было сосредоточено в Шварцвальде, где их производили кустарным способом, выпиливая зубцы вручную напильником в особом станочке, куда пропускалась непосредственно с бобины расплющенная предварительно проволока соответственного размера. Проволока употребляется английская, изготовляемая специально для этой цели, причем она получается обычно круглого сечения и прокатьюается в прямоугольное или слегка суженное кзади сечение на ручных вальцовых станках. В последнее время ручная работа вытесняется довольно примитивными машинами, к-рые изготовляются самими заводчиками и кустарями в Шварцвальде по собственньш чертежам. Хотя во время войны 1914 г. многие государства поставили у себя производство пилок для Л.,но до сих пор как в количественном, так и в качественном отношении доминирующее значение принадлежит полукустарному шварцвальдскому производству, л. Павпушков.

ЛОВУШКА, ловительное приспособление, прибор для улавливания: посторонних предметов тяжелее воды (камне-ловушки и песколовители), примесей, пла-вагопщх в воде или соке, напр. соломы,.бот-

вы и мезги (соломоловители), и жидких или твердых частиц, уносимых паровым или газовым потоком (соколовушки, маслоотделители и лаверы).

Л., применяемые в сахарной промышленности. Камнеловушки устанавливаются по пути движения свеклы на гидравлич. транспортерах леред свекломойками и после них; иногда конструктивно они представляют одно целое со свекломойкой. По своей конструкции они делятся на автоматические и механические. Типичным представителем первого вида является Л. системы Баранова, устанавливаемая в конце гидравлич. транспортеров и представляющая собою железный карман с наклонным дном. В нижнюю часть Л. под напором поступает вода. Действие Л. таково: свекла струей воды подбрасывается вверх, а камни собираются в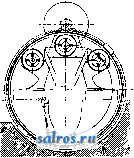

Фиг. 1.

кармане, скатьшаясь по наклонному дну„ откуда периодически удаляются при открывании шибера. Из механич. камнеловителей надо указать камнеловушку системы Эйк (Еуск), мойку системы Рауде и еевидоизмене-1ШЯ. Обе эти камнеловушки также устанавливаются на жолобе гидравлич. транспортера. Л. системы Эйк представляет собою решетчатый барабан, к-рый установлен вдоль транспортера (фиг. 1). Против барабана в дне транспортера имеется продолговатая щель, прикрываемая качающимся клапаном, регулирующим ширину щели. Балласт, камни, железные предметы и прочие тяжелые-загрязнения падают внутрь барабана, ковшами которого поднимаются и сбрасываются в лоток. Для устранения провалов свеклы в щель транспортера под напором поступает-вода, поднимающая свеклу вверх. Л. типа мойки Рауде состоит из железного цилиндра, с конич. дном, оканчивающимся шибером. Внутри цилиндра имеется вертикальный вал с насаженными на него лопастями, назначение которых перемешивать свеклу и направлять ее снизу вверх. Вал делает до 20 об/м. (в зависимости от диам. цилиндра). Камни попадаюпщеся в свекле, собираются в конич. -части Л.,откуда они удаляются через шибер.

Песколовители применяются для очистки известкового молока от камней и песка и для очистки соков,обработанных известью, от песка, попадающего в сок вместе с известковым молоком. Простейшим типозг песколовители является цилиндрич. дырчатое сито. Из песколовителей более совершенного типа необходимо отметить песколови-

тель, основанный на принципе отстаивания (сист.Русселя ,фиг.2) .представляющий собою полуцилиндрич. корыто, разделенное вертикальными перегородками на несколько отделений. Вдоль корыта вращается вал с прикрепленными к нему скребками, которые одной своей стороной скользят по дну корыта, а другой-по вертикальной стенке, образуя

Фиг. 2.

подобие ковшей, которыми осаждающиеся на дно корыта песок и мелкие камешки передаются из одного отделения песколови-теля в другое. Из последнего отделения камешки и песок удаляются при помощи шнека; неочищенное известковое молоко подается навстречу движению камней и песка.

С о л о м о л о в и т е ли служат для очистки свеклы от легких плавающих примесей- соломы,ботвы и пр.-и устанавливаются как перед свекломойкой, так равно и после нее. Обьганый тип соломоловителя - железные или деревянные грабли, установленные поперек гидравлического транспортера. По мере накопления примеси грабли очищаются вручную. Примером. механически очищающегося соломоловителя может служить Л. типа Шмитца, в которой уловленная зубьями грабель солома и ботва поднимаются и сбрасываются в ящик. Для полной очистки свеклы от соломы применяется соломолови-тель сист. Неселовского, представляющий собою подвижную наклонную плоскость (фиг. 3). Свекла скатьтается навстречу движению наклонной плоскости, а солома и зелень задерживаются проволочными гвоздями, насаженными в планки плоскос1ги, и удаляются с нижней части прибора струей воды.

Для освобождения диффузионного сока от JT?леченных частиц и волокон свеклы наиболее совершенным является самоочищающийся мезголовитель типа ПильгардТа, состоящий из вращающегося на валу ситчатого цилиндра, соединенного снизу с отводящей трубой и закрытого сверху. Ситчатый цилиндр окружен сосудом Б,кк-рому снизу примыкает воронкообразный придаток с отводящей трубой Г (фиг. 4). Внутри сосуда Б имеется ситоочиститель. Неочищенный сок поступает В; сосуд через отверстие А и проходит через турбинку В. которая насажена на вал сита.

Соколовушки устанавливаются на выпарных аппаратах для улавливания жидких частиц сока, уносимых паровым потоком. Л. построены на принципе уменьшения скорости движения, а также живой силы парового потока, несущего во взвешенном состояний жидкие частицы;, для этого паро-

Фит. 3.

вой поток направляют через обширно© замкнутое пространство, перегороженное одной-или несколькими дырчатыми переборками, о к-рые ударяется паровой поток и при по- тере скорости выделяет жидкие частицы. Того же эффекта достигают, заставляя паровой поток проходить между переборками, меняющими его направление. Примером Л., основанной на первом принципе, служит весьма распространенная горизонтальная Л. сист. Годека; примером Л. второго типа может служить вертикальная Л. и сепаратор, устанавливаемый на аппарате Кестнера.

Для удаления масла из отработавшего пара паровых машин, поступающего на обогревание различных приборов, применяются маслоотделители(см.),в которых паровой поток направляется в обширное замкнутое пространство, заполненное многочисленными переборками ,располо-женными вертикально и параллельно одна относительно другой.

Для очищения газового потока от пыли и

Фиг. 4.

Фиг. 5.

одновременно охлаждения газа применяется л а в е р (фиг. 5), состоящий из цилиндра, перегороженного поперек тарелками; тарелки перекрыты колпаками, на к-рые поступает сверхувода. Газ, всасьшаемый насосом, идет против воды, охлаждается и одновременно очшцается ею.

Л. в целлюлозном и бумажном производствах служат для улавливания из производственных сточных вод ценных млтериалов- волокна и наполняющих бумагу веществ (каолин, барит и т. п.). Содержание улавливаемых веществ в сточных водах выражается 0,05-0,08% и зависит главн. обр. от степени размола волокон массы в бумажном производстве и от характера варки целлюлозы- в целлюлозном. Количество стачных вод для среднего сорта бумаги колеблется в пре-дел&,х 60---100 л** на 1 т. Приведенная характеристика сточных вод определяет конструкцию Л. Это-или 1) большие отстойные резервуары различной формы, в которых

происходит разделение твердых вeп^ecтв и воды по уд. весу, или 2) фильтры с частьши сетками и сукнами большой фильтрующей способности.

; Фиг. 6.

Необходимыми условиями удовлетворительной работы Л. первого типа являются: достаточно большой объем резервуаров, непрерывная работа системы и отсутствие в поступающей сточной воде токов, мешающих осаждению частиц. Дорогостоящее со-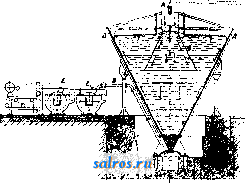

фит. 7.

оружение этих Л. оправдьшается дешевизной и простотой их эксплоатации. Примером этого типа Л. является скребковая Л. системы Фойт-Шмидта (Voith-Schraidt) с камерой объемом 900-1 200 л*, в к-рой отстоявшийся осадок непрерывно удаляется со дна камеры закрепленными на бесконечных цепях скребками в особый приемник, откуда масса насосом а (фиг. 6) возвращается обратно в производство. Сточные воды собираются в приемник, б ц наклонною поперечною перегородкою в направляются в нижнюю часть Л где и оставляют взвшпенные в воде частицы. Отстоявшаяся чистая вода через отверстия, 3 в, боковых стенках резервуара по-в ббкрвой, канал д и из него насосом

е удаляется в наружную сточную канаву, ф-ки или частично обратно в производство, заменяя нек-рое количество потребной для него свежей воды. Для фабрик с небольшим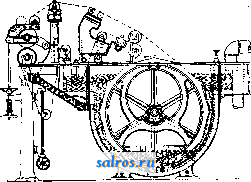

Фиг. 8.

расходом воды такие Л. неприменимы. Расчет Л.: на каждый ж' сточных вод в мину-* ту необходимо иметь 150 л* объема такой Л. Более^удобными отстойными аппаратами.

Чистая вода / Вапот

Ф

Фиг. 9.

работающими по ому же принципу, являются воронкообразные Л. (системы Франкач Фюльнера Шмидта, Кроцпа и др.). На фиг. ?

показана Л. сист. Фюльнера. Сточная вода поступает по трубе А и обратно поставленной воронке Б в верхЕсюю треть Л. Взвешенные частицы собираются в ее нижней части и под давлением выше стоящей воды по трубе В непрерывным потоком, регулируемым задвижкою или краном, возвращаются в производство. Отстоявшаяся вода по радиальным каналам Г и круговому Д также частью возвращается для разбавления массы в производство, а избыток направляется в сточную канаву. На фигуре показан случай, когда отстоявшееся волокно по трубе В направляется на картонную машину, где обезвоживается на двух последовательно поставленных обезвоживающих цилиндрах Sj, Е и отжатое затем между двумя прессовыми валами сходит с машины в виде сырых листов картона, подлежащих лишь окончательной сушке. Такие Л. малых размеров помещаются внутри фабричного корпуса, а больших-иногда и за его стенами.

Сюда же принадлежат механич. сетчатые фильтры различных систем. На фиг. 8 показана Л. сист. Фюльнера. Массоловка состоит из цилиндра, покрытого сукном и вращающегося в ванне со сточной водой. Вода проходит через сукно, а волокна остаются на его поверхностп, верхняя часть которой находится над уровнем воды, С сукна масса снимается валиком, обтянутьш суконным чулком, с которого она счищается шабером в установленный под ним жолоб. Наиболее совершенной конструкцией механич. фильтров, употребляемых в качестве Л., являются секционные вакуум-фильтры (фиг. 9), характерные данные к-рых приведены в табл.

Характерные данные секционных вакуум-фильтров.

Содершание волокна в мв/л . . Колич. сточных вод в л з на 1 .w2 площади Л. . . . % удержанного

волокна .....

Содержание су! хих веществ в i массе в % ...

Л.-фильтры за исключением тех, к-рые принимают волокно сукнами, мало удерживают т. н. наполняющие вещества, т. е. минеральные примеси, прибавляемые к бумажной массе для частичного заполнения пор между волокнами бумажного листа. ю. Деииоов.

Лит.: см. Бумажное производство.

ЛОВЧИЕ КОЛЬЦА, ловчие пояса, применяют для борьбы с некоторыми вредителями в плодоводстве. Стремление насекомых прятаться для окукливания или на зимовку (под отставшие чешуи коры и в тре-пщны на стволе плодового дерева) используется плодоводами применением Л. к. Перед наложением на деревья Л. к. с целью привлечения в них насекомых необходимо уничтожить все естественные убежища вредите-.пей путем очистки ствола дерева от старых отставших частей коры и лишайников и сде-

лать затем побелку (обмазывани е) ствола и главных сучьев глиной с известию. После такой подготовки дерева на него накладывают (под кроной или при основании) Л. к. шириной 16 см. В качестве материала для Л. к. служат: специальная гофрированная бумага, солома, рогожа, тряпье, простад бумага, предварительно сложенная гармоникой, мох, опавшие листья, древесная, в особенности упаковочная, стружка (последние три материала сверху покрываются не промокающей от дождя бумагой). Л. к. привязывают к дереву мочалой, бечевкой или мягкой проволокой, но неплотно, чтобы оставались щели для проникания под пояса вредителей. Сроки накладки и снятие Л. к. зависят от биологич. особенностей вредителя и географич. положения района. Л. к., осторожно снятые с деревьев, сжигают вместе с заключенными в них вредителями или обваривают кипятком. Чаще всего Л. к. применяются против плодожорки и нек-рых долгоносиков, в. Болдырев.

Лит.: см. Вредители в сельском хозя й с т ве.

ЛОГАРИФМ, показатель степени, в к-рую нужно возвести основание (постоянное положительное число), чтобы получить данное число. Обозначив основание Л. через а и Л. данного числа N через у, получаем

или

Свойства Л.: 1) Л. произведения равен сумме Л. сомножителей; 2) Л. дроби равен разности Л. числителя и знаменателя; 3) Л. степени равен по- /, казателю степени, умноженному на логарифм возводимого количества (корень рассматривается здесь как дробная-степень); 4) Л, единицы равен нулю; 5) Л. основания равен 1. Обьпс-новенно предполагается а > 1. Считая данное число X переменным и обозначая его Л. через у, определяем логарифмическую ф-ию 2/ = Iga ж. Из определения Л. следует: х=а^. Ф-ия а (степень с постоянным основанием и переменным показателем) называется показательной ф-ией. Она является обратной логарифмич. ф-ии. Ф-ия y=lgaX определенна только для положительных значений х (см. фиг.); при а > 1 это ф-ия возрастающая, ее значения для х<1 отрицательны, для х> 1 положительны,

Иш lg .ж = - оо, Иш Iga ж = -Ь со.

Определение Л. для отрицательных и комплексных значений аргумента-см. Функции комплексного переменного.

Связь между Л. при различных основаниях. Пусть у = Ig х, т. е.

== X. Логарифмируем это равенство при основании Ь:

lgbX=yl?ba= IgaX Отсюда при х = Ъ получаем: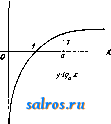

Производная логарифмич. ф-ии, см. Диференциальное исчисление. Л, при основании

е=Ип1 + = 2,71828 ...

назьшается натуральным и обозначается In ж (Igg ж).Натуральные Л. являются в ряде вопросов анализа наиболее простыми,

/dx - И пелого

ряда других интегралов (см. Интегральное исчисление).

Десятичные Л. При вычислениях обычно употребляются Л. с основанием 10. Такой Л. будем обозначать: lga;(lgioa;). Из определения Л. следует: Ig 1 = 0, Ig 10=1, lgl00 = 2,Ig0,l=-1, lg0,01 = -2, ...Из свойства возрастания следует: десятичный Л. числа, заключенного между 1 и 10, имеет целую часть (характеристику Л.), равную О, при 10 < JV < 100 характеристика IgJV равна 1, и вообще, если число цифр до запятой есть к, то характеристика Л. = fe-1. Дробная часть Л. называется мантиссой. Л. чисел, имеющих одинаковые значащие цифры, имеют одинаковые мантиссы. Таблицы де-С51тичных Л.обьпсновснно дают мантиссы для чисел от 100 до 999 (четырехзначные Л., т. е. дающпе приближенное значение мантиссы с 4 знаками) или от 1 ООО до 9 999 (пятизначные Л.). Если число значащих цифр данного исла больше, чем дано в таблице, то мантисса находится при помощи интерполяции (см. Вычисления приближенные). Для нахождения числа по Л. можно пользоваться той же таблицей, находя в ней две мантиссы, ближайшие к данной, и применяя интерполяцию; для той же цели существуют таблицы антилогарифмов, где аргументом является мантисса, а функцией-значащие цифры искомого числа. Таблицы Л. употребляются для умножения, деления, возведения в степень и извлечения корня из чисел; при логарифмировании эти действия заменяются соответственно более простыми-сложением, вычитанием, умножением и делением. Для многих других ф-ий (напр. тригонометрических) также часто даются значения не самих ф-ий, а их Л., для удобства последующих умножений и делений значений этих функций.

Имеются таблицы, которые дают возможность найти по Л. двух чисел Л. их суммы или разности. Предположим а>Ь; имеем:

lg(a+Ь)= lga-blg(l + ).

Обозначим

lg - Ig b = А, Ig (l + = Ig (l -Ь 10~) = B.

Достаточно составить таблицу, дающую В как ф-шо А, чтобы вычислить: Ig (а+ Ь) = Ig a-j-B.

Аналогично: Ig (а - Ь) = Ig а + Ig 1 - или,

принимая Iga-Ig ) =В, получаем: lg(a-&)=

= lg a-lg в; положим 131i /o:b=C,ot-

куда 10 -В-Ь10-с=1.Имеем: Ig(а-Ь) = Igа-С. Замечая, что В н С связаны симметричным

соотношением, можем ограничиться Таблицей, дающей значения В, при к-рых 10 < ;

В> 0,30103; для меньших значений нужно переменить роли В и С.

Для натуральных Л. существуют специальные таблицы. Но можно вычислять натуральные Л. по десятичным и обратно при помощи ф-лы:

lncc=lga;-lnlO,

или

lga;= 1пж- Ige. Число ilf=lg 6 = 0,43429... назьшается модулем; число In 10= j = = 2,30259...

Ф-лы для вычисления Л.-см. Ряды, Вычисления приближенные.

Лит.: Успенский Я. В., Очерк истории логарифмов, Петроград, 1923; П р ш е в а л ь с к и й Е., Пятизначные таблицы логарифмов и тригонометрич. величин, М.-Л., 1928; Гон фен В., Логарифмы и антилогарифмы в упрощенных таблицах, М., 1919; Афанасьев А. П.,Таблицы математич. и физич. величин. П., 1923. В. Степанов.

ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА, прибор, служащий для производства вычислений, обычно совершаемых при помощи таблиц логарифмов. Пусть у = f(x) представляет ненрерьшную однозначную функцию переменного X, возрастающую в рассматриваемом промежутке изменения х. Составим таблицу значений этой функции для последовательного ряда обычно равноотстоящих значений аргумента и нанесем их на линейку в виде отрезков, имеющих общее начало. Против полученных т. о. точек надпишем соответствующие значения аргумента. То же самое проделаем по отношению к другой функции Z = (p{t) такого же рода, нанеся ее значения на другую линейку. Приложим две полученные нами шкалы одну к другой. Пусть начальная точка второй шкалы совпадает с точкой Хх первой шкалы, а какая-нибудь ее точка t с точкой х^; тогда очевидно наши шкалы могут служить для решения уравнения f{x+4>{) = /(жа) относительно одной из трех величин жх, жа, * по заданным двш. Предположим в частности, что обе функции f и 9? представляют логарифм. Уравнение примет вид:

lgжl-Ьlg*= lg 2, откуда x-J,=x и у = Ж1, т. е. наши линейки дают возможность находить произведение и частное двух чисел.

Построенная на этом принципе Л. л. имеет почти ту же давность,как и сами логарифмы. В 1620 г., через 6 лет после опубликования Непером его Mirifici Logarithmorum Cano-nis Descriptio, Гюнтер предложил прибор, отличающийся от приведенной выше схемы лишь тем, что роль второй линейки играл циркуль, а еще 10 лет спустя Отред (Ought-red) воспользовался уже двумя линейками. С тех пор усовершенствовались лишь детали, пока в 1850 г. Мангейм не выработал того типа линейки, который с незначительными изменениями повторяется и сейчас целым рядом фирм: А. W. Faber, А. Nestler, W. F. Stanley, J. Davis, Gebr. Wichmann и др. Эта Л. л. (фиг. 1) имеет две неподвижные шкалы^У и JJi, между к-рьши перемещается подвижная часть ее (движок) с двумя

шкалами N и N\j нанесенными на ее лицевой стороне, и тремя шкалами S, Т ж L, нанесенными на ее обратной стороне. Шкала JV делится на две равные части, каждая из к-рых принята за единицу длины и к-рые повторяют одна другую. На этих шкалах отложены отрезки, пропорциональные значениям логарифмов чисел от 1 до 10 (Ig 1=0- начало шкалы, lglO=l-конец пшалы), причем число промежуточных делений дается в зависимости от размеров Л. л.; так например, на Л. л. в 25 cjm в промежутке от 1 до 2 деления д^ны через 0,02, в промежутке от 2 до 5-через 0,05 и в промежутке от 5 до 10-через 0,1. Шкала N тождественна

соответствующей множимолгу, начало шкалы на шкале JVi против черты шкалы N\, соответствующей множителю, читаем произведение. В том случае, когда множитель придется вне шкалы N-i за этой последней надо вообразить ее повторение, иначе говоря, совместить с множимым на шкале Ny конечную черту шкалы N\ и прочитать произведение на шкале против черты шкалы JV], соответствующей множителю.Число знаков п произведения, стоящих влево от запятой, как известно или единицей меньше суммы числа знаков целой части множимого их и множителя или равно этой сулше. Этим двум возможностям со-

Фиг. 1.

со шкалой N. Шкала повторяет одну из шкал N во вдвое большем масштабе и соответственно этому с более частыми делениями. Наконец шкала тождественна со шкалой Деления шкалы S соответствуют значениям 2-1- Ig sin X для значений х от 34 до 90° (sin 34 = 0,01 и следовательно Ig sin 34 -2, Ig sin 90° = 0) и отмечены значениями аргумента ж; деления шкалы Т соответствуют значениям 1-f Igtgx для значений х от 5°44 до 45° (tg5°44 = 0,l и следовательно Ig tg 5°44 = - 1, Ig tg 45° = 0) и тоже отмечены значения аргумента х. Наконец шкала L дает значения логарифмов чисел. Л. л, снабжена визиром, состоящим из передвигающейся вдоль нее рамки со стеклом, на к-ром нанесены 1 или 3 перпендикулярные Л. л. черты. При трех чертах на визире обе крайние отстоят от средней на расстояние, равное Ig в масштабе шкалы N\ это дает возможность, двигая одним визиром,

решать задачи типа /=- и d =

Визир облегчает оценку долей делений, дает возможность производить отсчеты по шкалам, не лежащим непосредственно одна около другой, и служит для фиксирования промежуточных результатов при сложных выкладках. При пользовании Л. л. надо помнить, что увеличение или уменьшение числа в 10, 100, 1 ООО ,... раз не изменяет мантиссы логарифма числа, а влияет только на характеристику. Поэтому, с одной стороны, каждую из шкал N, можно представить себе повторенной вправо и влево отфак-тически имеющейся шкалы, а с другой стороны, читать нанесенные на шкалах числа в зависимости от обстоятельств различно, напр. 2 можно читать как 0,2; 2; 20; 200 и т. д.

Умножение производится при помощи шкал NiuNi. Совмещая с чертой шкалы JVi,

ответствуют два слчая отсчета произведения, а именно, при совмещении с множимым начала шкалы движка w=wi-bna~l, при совмещении конца шкалы n = ni+nz. Деление производится на тех же шкалах, но теперь с чертой шкалы Ni, соответствующей делимому, совмещается черта шкалы N[, соответствующая делителю. Частное читается па шкале Ni против начальной или конечной черты шкалы Щ в зависимости от того, которая из них придется против шкалы Ni. В первом случае число знаков целой части частного единицей больше разности числа знаков делимого и делителя, во втором оно равно этой разности. Возведение в квадрат и извлечение квадратного корня основано на известных

соотношениях Ig = 2 Ig ж и Ig ж = а > которые осуществляются шкалами N в. N. Квадрат читается на шкале N против основания степени, отложенного на шкале Nx, обратно-корень квадратный-читается на шкале Ni против подкоренной величины, отложенной на шкале N. Комбинирование возвышения в квадрат с умножением и извлечения квадратного корня с делением дает возможность находить кубы и кубич. корни.

Назначение шкал S п Т двояко: во-первых, давать значения sin и tg в промежутках, указанных выше, во-вторых, производить вычисления, при к-рых sin и tg входят множителями и делителями. Действительно, совмещая начальные черты этих шкал с начальными чертами шкал N к Ni, имеем на этих последних против делений 8 и Т соответствующие значения sin и tg, причем первая половина N дает sin от 34 до 5°44, вторая-от 5° 44 до 90°. При вычислениях с sin и tg шкалами S и Т пользуются так же, как обычной логарифмич. шкал ой, с тою только разницей, что шкале <S всегда соответству-

ет шкала N, а шкале Г-шкала Ni. Более сложные вычисления требуют нахождения логарифмов чисел; для этой цели служит шкала L обратной стороны подвижной части линейки. Л. л. описанного типа изготовляются длиной 12,5, 25, 50 и даже 100 см и применяются в зависимости от требуемой точности. Допуская возможность отсчета до 0,1 мм, получим для Л.л. в 25) см погрешность от 1,5 до 3%.

Нарящу с' описанным типом Л. л. постепенно выработался ряд Л. л. специального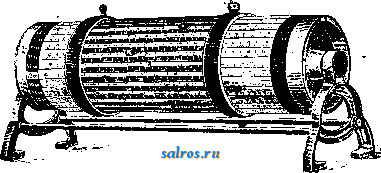

Фиг. 2.

назначения. Прецизионная линейка при длине в 25 см дает точность Л. л. в 50 см благодаря тому, что на ней все шкалы разбиты пополам и каждая половина занимает всю длину Л. л. Прием вычисления при помощи этой Л. л. несколько сложнее, чем на обыкновенной Л. л. Далее изготовляются Л. л. со специальными шкалами, построен-ньши по изложенному выше (в начале статьи) принципу и приспособленные для электротехнических, гидравлич., машиностроительных, железобетонных и других технрт-ческих расчетов. Параллельно с разработкой и усовершенствованием Л. л. описанного типа делались попытки построения по тому же принципу других приборов в целях достижения или большей точности или большей компактности прибора. Из этих попыток заслуживают упоминания прибор Фул-лера, дающий результат с точностью до 4 или даже 5 знаков, в к-ром шкала нанесена по винтовой линии на цилиндре и имеет длину свыше 25 л*, и прибор Boucher, усовершен-етвованный Stanley, имеющий вид карманных часов, в к-ром шкалы нанесены након-центрич. вращающихся циферблатах и точность к-рого соответствует точности Л. л. в 25 см. В последнее время для более точных вьгаислений применяют т. н. счетные вальцы (Rechenwalzen), представляющие собой отдельные участки Л. л., нанесенные по образующим цилиндрич. вальца (фиг. 2); дви-зкок в этом случае имеет форму полого цилиндра с окнами, прорезанными против основных шкал; деление движка нанесено по краям этих прорезов. Вальцы позволяют производить операции умножения и деления с такой же быстротой, как и при помощи обычной Л. л., но с точностью в 10-100 раз большей.

Лит.: Абрамов Н. М., Технич. вычисления. М., 1928; П а в .л о в Н. Н., Производство технпч.

вычислений, 2 изд!, М., 1927; Филиппов В. М., Теория и практика элементарных приближенных вычислений, СПБ, 1909; Франк М. Л., О решении трехчленных уравнений при помоши логарифмической линейки, Сборн. ИИПС , Петроград, 1915, т. 89 С а j о г i F., А History of tbe Logarithmic Slide Rule, London, 1909; dO с a g n e M., Le calcul-simplifie par les proc6d6s mecaniques et graphitiues, 2 ed., Paris, 1905. H. Меликов.

ЛОГАРИФМИЧЕСКИЕ ДИАГРАММЫ, частный вид номограмм с неравными делениями, шкал, когда деления последних пропорциональны логарифмам чисел, обозначающих точки деления (см. Номография). Построение Л., д. основывается на следующих принципах. Пусть имеется равенство

у=Ъ + х, (1) где у лх-нек-рыепере-менные, а &-постоянная, величина. В некоторой прямоугольной системе осей координат ур-ие (1) представится графически в виде прямой, у к-рой угол наклона с положительным направлением оси абсцисс равен 45° и которая отсекает на оси ординат считая от начала координат, отрезок, равный Ь. Меняя затем параметр Ь, придавая ему значения Ъ^, Ъ^, b , получим семейство параллельных прямых, отсекающих на оси ординат отрезки Ъ^, bg, Ь„. Нетрудно видеть,что, взяв на какой-либо из этих прямых y=bv-\-x точку М с координатами I и ?, имеем:

Vbv + . (3)

Т. о. для того, чтобы сложить при помощи полученной номограммы два числа $ и bv, нужно поступить след. образом. Взяв на оси Xточку, соответствующую числу про-

67+73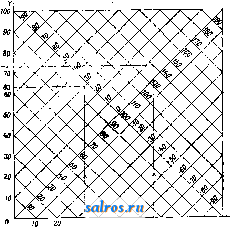

30 W 50 60 1-7(7 33-30 67-73

Фиг. 1.

водят через эту точку перпендикуляр к оси X до встречи с наклонной (диагональной) прямой, имеющей параметр, равный другому слагаемому Ъу, и затем из этой точки встречи опускают перпендикуляр на ось Y.

Число, cooTBerCTByis основанию этого перпендикуляра, при условии равенства масштабов делений осей координат, и дает искомую сумму (фиг. 1). На практшад обычно пользуются готовой сеткой, что освобо-гкдает от необходимости проведения вышеупомянутых перпендикуляров. Если вместо (1) имеется равенство

у=Ь-х, (3)

или

г/ + ж=ь, (3)

то при различных значениях Ъ получаем семейство прямых, наклоненньи: к положительному направлению оси X под углом 135°. Взяв на какой-нибудь из этих прямых y+x = bv какую-либо точку, имегошую координаты Jj и f, получим:

г/ + r=bv. (4)

Т.о. для того чтобы найти при помощи второго семейства наклонных прямых сумму двух слагаемых г} и следует через точки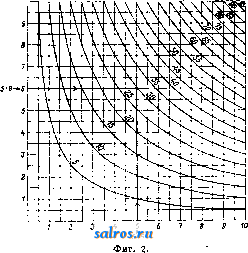

деления и на осях координат восставить к последним перпендикуляры и определить параметр bv той наклонной прямой, которая проходит через точку пересечения перпендикуляров (фиг. 1).Вычитание можно производить способами, обратными вышеуказанным. Пусть имеется далее ур-ие:

жг, = а, (5)

где X и 2/-попрежнему переменные, а а- постоянная величина. Графически ур-ие (5) представляется в прямоугольных координатах равнобокою гиперболою с асимптотами, совпадающими с осями координат. Меняя затем величину параметра а, придавая ему значения а-, а^,а„, получим семейство равнобоких гипербол; при помощи этой номограммы можно производить умножения и деления чисел (фиг. 2). Недостаток этой номограммы заключается в том, что если пересечение перпендикуляров не находится на одной из имеюнщхся на номограмме кривых, то приходится либо вьгаерчивать соответствующую новую кривую либо определять параметр последней на-глаз, в ущерб конечно точности получаемых результатов. Для

устранения указанного недостатка применяют номограмму, в которой кривые (гиперболы) заменены прямыми, проведение которых не представляет конечно таких затруднений, как проведение новых кривых. Пусть имеется равенство:

у = ах. (6)

При определенном значении параметра а равенство (6) представляет прямую, прохода г

Фиг. 3.

дящую через начало Координат и тангенс угла наклона которой с положительным направлением оси X равен а. Меняя значения параметра а, получаем пучок прямых, проходящих через начало координат. Из (6) видно, что для того чтобы умножить два числа а?! и а^, нужно взять на оси X точку, соответствующую числу х-, и провести череа эту точку перпендикуляр к оси X до пересечения с наклонной прямой, имеющей параметр а^; ордината полученной точки^пере-

д 4 Фиг. 4.

5 6 1 а 9 10

сечения и определяет искомое произведение (фиг. 3). Но, устраняя один недостаток (замена параметренных кривых прямыми), последняя номограмма обладает новыми недо-

статками, делающими ее мало пригодной для практич. применения и заключающимися в следующем: 1) если сомножители близко подходят к пределам х я у номограммы, то точки пересечения выходят за пределы номограммы; так, для того чтобы умножить 10 на 10, необходимо, чтобы высота номограммы была в 10 раз больше ее основания;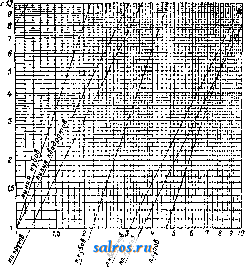

Фиг. 5.

2) пересечение прямых, перпендикулярных оси X, с наклонными прямыми, б.тизко подходящими к оси Y, происходит под очень острым углом, вследствие чего делается почти невозможным б. или м. точное определение точки пересечения прямых; 3) в области, близкой к начальным значениям х та. у, имеет место скопление диагональных прямых, вследствие чего затрудняется отсчет.

Для того чтобы сохранить все преимуще-ства прямолинейных номограмм и устранить в то же время вьппеприведенные недо-статки их, прибегают к Л. д., или логарифмическим номограммам, принцип построения к-рых заключается в <У1едующем. Взяв логарифм от обеих частей <5), имеем равенство:

Iga?-big 2/= Iga, (7)

форма которого тождественна с формой равенства (3)j вследствие чего для (7) можно построить номограмму, аналогичную номограмме фиг. 1. Для этой цели следует отложить на осях координат в одинаковом масштабе отрезки, пропорциональнью логарифмам поставленных у делений чисел. Соединив точки одинаковых делений на осях координат диагональньпли прямыми и отметив у каждой из них число, поставленное у деления, получим Л. д., которая может бьпъ применена как для умножения, так равно и для деления чисел (фиг. 4). Для умножения м. б. применены два способа, в зависимости от того, пользуются ли при этом диагональными прямыми, идущими под углом 45 или 135** к положительному направлению оси X. Умножение и деление, сведенные к сложению и вычитанию логарифмов, производят-

ся таким же образом, как это было описано вьппе для номограммы фиг. 1.

Л. д. очень удобны для получения ф-ий степени или корня какой-либо переменной, в особенности если степени и корни дробные. Ур-ие у=х^ напр. м. б. представлено еще и следующим образом: Ig 2/=3 Ig х, что имеет вид г?=3. Отсюда следует, что, проведя по сетке с логарифмич. делениями прямую через начало координат, имеющую тангенс угла наклона к положительному направлению оси X равный 3, получим т. и. л и н и ю кубов (фиг. 5), т. е. прямую, ординаты точек к-рой равны кубам соответствующих абсцисс. Для построения линии кубов достаточно верхнее и нижнее основания квадратной Л. д. разделить на три равные части и соединить точки деления О, 1, 2 нижнего основания соответственно с точками деления 1, 2, 3 верхнего основания. Аналогично можно построить линию любой степени п.

100Н

зон

-0,06-0,05-

0,03-

.! i

W 100 Фиг. 6.

300 и hi

независимо от того, будет ли п числом целым или дробным. Во всех случаях тангенс угла наклона диагональных прямых должен равняться п. Л. д. применяются во многих областях техники, как напр. в сопротивлении материалов, деталях машин, электротехнике и т. д. Примером Л. д. служат диаграммы для расчета винтов аэропланов.

Лит.: Астафьев А., Применение методов номографии, СПБ, 1909; Волков А., Математические основания номографии, М., 1911; Герсеванов Н., Основания номографич. исчисления, вьшусч. 1, СПБ, 1906, выпуск 2, СПБ, 1908; П е д л Дж., Построение и применение номограмм, Москва, 1913: М е h m к е К., NuraeriSches Rechnen, Enzyklopadie d. mathemat. Wissenschaften, B. 1, T. 2, H. 6-7, В.-Lpz., 1901- 1902, p. 1006-1052; Mehm ke R., Neue Methode be-liebige numerisclw Glelchungen mit elner Unbekannten graphisch aufzuldsen, CivilingpniPur , В., 1889; R о us с h 1 e C.,Graphisch-mechanlscheMethode z.Aufiesung d. numerlschPn Glelchungen, Stuttgart, 1884; Schilling F., tJber d. Nomographic von M. dOcagne, Lpz., 1917; Go ed see Is, Les precedes pour sim-рНПег les calculs, Bruxelles, 1898; dOcagne M., Traite de nomographie, 2 ed., P., 1899; dO с a g n e M., Le calcul simptifie par les precedes m6caniques et graphigues, Paris, 1905; dOcagne M., Calcul gra-phiqiie et nomographie, P., 1910; S о r e a u R., Contribution h la th6orie et aux applications de la nomographic, Memoirs et comptes rendus des travaux de la Societfe des ingen. civUs de France*, P., 1901; P e s с 1 G., Cennl di nomografia, Livorno, 1901. M. Серебренников.

Логарифмические диаграммы в авиации широко применяются как для расчета винтов, так и аэроилацов; они предложены сотрудником лаборатории Эйфеля Ритом (Rith). Винтовые Л. д. строят на логарифмич. бумаге, откладывая по осям с логарифмич, шкалами координаты:

и

,60 V ~ 3,6 nD

где -нмшцност в Н*, п-число оборотов винта в МНЕ., JD- диаметр его в м, v-ско-pooib в ш1ч, Q-массовая плотность среды в ш mjM* (фиг. 6). На полученной кривой делают разметку величин кпд ?. Взяв некоторые средние практические величины, для п, Л ш Q, на шкалах л и наносят параллельные шкалы v kN. На той же номограмме наносят шкалы для п и D с наклонами /i и 6/i к шкале Д (v) (фиг. 7). На этих шкалах особо выделяют точки с отметками п и D, принятые за средние, и обозначают знаком 0 (origine-начало). Расчет по Л. д. ведется так: строится ломаная, состоящая из отрезков v, п, D и N (фиг. 7) в том или ином порядке; конец ломаной, должен лежать на характеристич. кривой винта, дающей зависимость /3 от А (см. Возд/шмыйвинт); при помощи указанной ломаной можно решать целый ряд задач по слодугощей схеме:

ра получим п и Г] при скорости v. Тяга вычисляется по ф-ле:

ф = 75-8,6.7-iV V

Взяв несколько скоростей v, получают полную характеристику винтомоторной группы. Характеристики для высоты z получаются так же, но на характеристике мотора откладывают фиктивные мопщости Мф ~, где

Л-отношение плотности на высоте г и на земле. Таким путем исследуются все волро-

Схемы решения этих задач даны на фиг. 8. Особенно удобны Л. д. серии винтов. В этом случав на диаграмму наносят все характеристич. кривые семейства, и точки с одинаковыми Г/ соединяют плавными кривыми. На диаграмме получается два семейства кривых р = Const (р-переменный параметр серии; обыкновенно берут за такой параметр

Л = , где Я-шаг винта) и = Const. Имея

такую диаграмму, легко для определенного задания (обычно N, п, v) подобрать винт с наибольшим Г}, меняя длину отрезка В (или п) таким образом, чтобы он касался одной из кривых *j = Const в своей конечной точке. В этой точке получим D, р та.п для наилучшего винта. Для построения характеристики винтомоторной группы (см. Аэродииймша) аэропланов берут винтовую Л. д. (фиг. 9); на особом куске кальки Т проводят ось v, а затем из произвольной точки ее а ведут отрезок аЬ # D; через точку Ъ проводят линию, пап, и размечают на ней Из полученных точек Ж, взятые из ха-

Фиг. 8.

сы, связанные с нзением работы винтомоторной группы.

Логарифмические поляры аэропланов строятся на основании ур-ий:

И

75Л^=д4J=C.4з',)

где 0~вес самолета в %г, N- потреб, мощность в HP, /S-площадь крыльев вм\ Q-массовая плотность среды в кг ск/м*, V-скорость самолета в км/ч, Су и Сх-коэфициенты подъемной силы и лобового сопроти-вления(см. Аэродинамика) аэропланов. По осям логарифмической бумаги наносятся шкалы и Ry, на тех же осях наносятся параллельные шкалы 2 ? и G, получаемые из. предьщущих формул при определенном 1; = г?!. На этой же номограмме наносят шкалы и w (фиг. 10) с наклонами */з и 1 не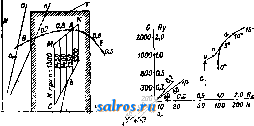

Фиг. 9.

Фиг. 10.

Фиг. 7.

раллельную шкале числа оборотов п. откладывают отрезки

рактеристики мотора, в масштабе шкалы N. Кривая МК дает логарифмич. характеристику мотора. Совмещая точку а кальки с любой отметкой v на диаграмме, в точке пересечения А характеристик винта и мото-

отношению к оси R-c (JV), на шкалах выделяют точки = г?1 и п=1, отмечая их знаком Or. Нанося кривую Ry в зависимости от 7?. и отмечая на ней углы атаки а°, по-л^-чим логарифмическую поляру аэроплана. Шкала п служит для исследования влияния подобного изменения крыльев самолета в п раз. Ломаная линия из отрезков JV, G, и те, отштадьшаемых в любом порядке, должна кончаться на поляре. Путем, аналогичным описанному выше, решается ряд задач при трех заданных и двух ис-комьк величинах из числа пяти переменных N, G, н, V ж а ж ряд задач, связанных с изменением масштаба м. Таким же путем